
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Приклад 1.14
|
|
|
|
Приклад 1.13.
Приклад 1.11.
Інтегрування частинами.
Теорема. Нехай на проміжку Х визначені та диференційовані функції  та
та 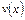 , причому
, причому 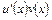 має первісну на цьому проміжку. Тоді має місце рівність.
має первісну на цьому проміжку. Тоді має місце рівність.
 .
.
1. Коли 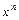 множиться на одну з функцій:
множиться на одну з функцій:  ,
, 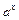 ,
,  ,
, 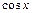 . Причому
. Причому 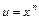 , dv – це функція. Щоб знайти dи, треба знайти похідну і помножити на dх. Щоб знайти v, треба знайти первісну (С= 0).
, dv – це функція. Щоб знайти dи, треба знайти похідну і помножити на dх. Щоб знайти v, треба знайти первісну (С= 0).
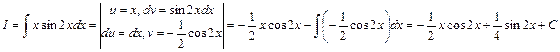 .
.
2. Коли присутні логарифми. Причому 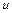 – це логарифми, dv – решта виразу.
– це логарифми, dv – решта виразу.
Приклад 1.12. 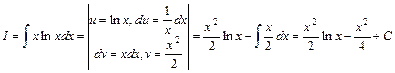 .
.
3. Коли присутні арки. Причому 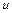 – це арк, dv – решта виразу.
– це арк, dv – решта виразу.
 .
.
4. Мішані.
 .
.
 .
.
Тема 2. Інтегрування раціональних виразів.
1. Поняття раціональних функцій.
До раціональних функцій відносяться многочлени та дробово-раціональні функції.
Означення 2.1. Многочленом степеня п називається вираз вигляду 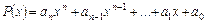 (
(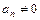 ), де х – змінна,
), де х – змінна,  – сталі числа.
– сталі числа.
Приклад 2.1. 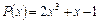 ,
, 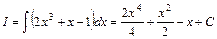 .
.
Означення 2.2. Дробово-раціональною функцією називається відношення двох многочленів. 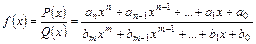 (
(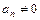 ,
, 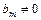 ).
).
Приклад 2.2. 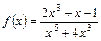 .
.
Означення 2.3. Дріб називається правильним, якщо степінь чисельника менший за степінь знаменника ( ); та неправильним, якщо степінь чисельника більший або рівний за степінь знаменника (
); та неправильним, якщо степінь чисельника більший або рівний за степінь знаменника ( ).
).
У будь-якому неправильному дробі можна виділити цілу частину (многочлен) і тоді неправильний раціональний дріб можна представити у вигляді суми цілої частини і правильного раціонального дробу.
Приклад 2.3. 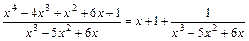 .
.
Приклад 2.4. 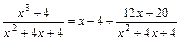 .
.
Приклад 2.5. 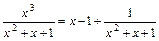 .
.
2. Інтегрування елементарних дробів.
1. 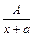 , де А, а – сталі числа, х – змінна.
, де А, а – сталі числа, х – змінна. 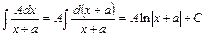
2. 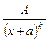 , де
, де 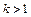 .
. 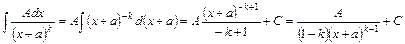
3. 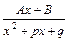 , де
, де 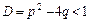 .
.
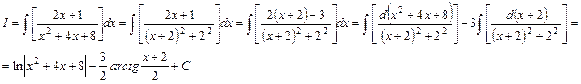
3. Інтегрування раціональних виразів.
Довільний дробово-раціональний дріб можна розкласти на елементарні дроби.
Приклад 2.6. Обчислити інтеграл 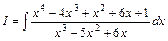 .
.
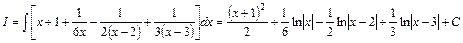 .
.
Приклад 2.7. Обчислити інтеграл  .
.
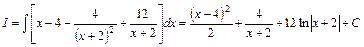 .
.
Приклад 2.8. Обчислити інтеграл 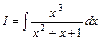 .
.
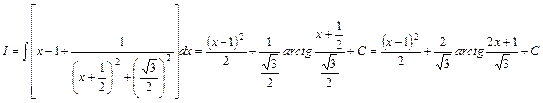 .
.
4. Інтегрування тригонометричних виразів.
Нехай є вираз, що залежить від синуса та косинуса 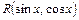 .
.
1. Якщо 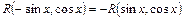 , то
, то  .
.
Приклад 2.15.  .
.
2. Якщо 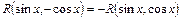 , то
, то 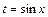 .
.
Приклад 2.16. 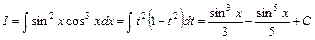 .
.
3. Якщо 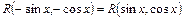 , то
, то 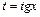 .
.
4. Якщо жодна рівність не виконується, то  ,
, 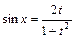 ;
; 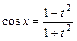 .
.
5. Інтегрування ірраціональних виразів.
1.  , заміна
, заміна 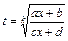 .
. 
2.  , заміна
, заміна 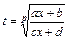 , де р – НСК.
, де р – НСК. 
3. 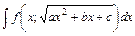 – підстановки Ейлера.
– підстановки Ейлера.
Якщо а >0, то  . Якщо с >0, то
. Якщо с >0, то 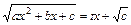 . Якщо α – корінь, то
. Якщо α – корінь, то 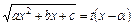 .
.
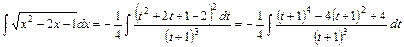
4. 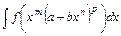 – підстановки Чебишова.
– підстановки Чебишова.
Якщо р – ціле число, 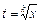 , де k – НСК знаменників т і п. Якщо р – не ціле число,
, де k – НСК знаменників т і п. Якщо р – не ціле число,  – ціле число,
– ціле число, 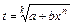 , де k – знаменник числа р. Якщо р,
, де k – знаменник числа р. Якщо р,  – не ціле число,
– не ціле число, 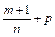 – ціле число,
– ціле число, 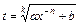 , де k – знаменник числа р. Якщо жоден випадок не підходить, то інтеграл не береться.
, де k – знаменник числа р. Якщо жоден випадок не підходить, то інтеграл не береться.

Тема 3. Визначений інтеграл.
1. Задачі, що приводять до поняття визначеного інтегралу.
|
|
|
|
|
Дата добавления: 2014-12-24; Просмотров: 317; Нарушение авторских прав?; Мы поможем в написании вашей работы!