
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
СТАТИСТИКА 3 страница. Естественно, базисное и цепное среднее относительное изменения должны быть одинаковыми и сравнением их с критериальным значением 1 делается вывод о характере
|
|
|
|
Естественно, базисное и цепное среднее относительное изменения должны быть одинаковыми и сравнением их с критериальным значением 1 делается вывод о характере изменения явления в среднем: рост, спад или стабильность. В нашей задаче 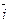 =
= 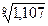 = 1,0114, то есть ежегодно в среднем смертность от болезней системы кровообращения растет в 1,0114 раза.
= 1,0114, то есть ежегодно в среднем смертность от болезней системы кровообращения растет в 1,0114 раза.
Вычитанием 1 из среднего относительного изменения образуется соответствующий средний темп изменения, по знаку которого также можно судить о характере изменения изучаемого явления, отраженного данным рядом динамики. В нашей задаче  = 1,0114 – 1 = 0,0114, то есть ежегодно в среднем смертность от болезней системы кровообращения растет на 1,14%.
= 1,0114 – 1 = 0,0114, то есть ежегодно в среднем смертность от болезней системы кровообращения растет на 1,14%.
Проверка ряда динамики на наличие в нем тренда (тенденции развития ряда) возможна несколькими способами (метод средних, Фостера и Стюарта, Валлиса и Мура и пр.), но наиболее простым является графическая модель, где на графике по оси абсцисс откладывается время, а по оси ординат – уровни ряда. Соединив полученные точки линиями, в большинстве случаев можно выявить тренд визуально. Тренд может представлять собой прямую линию, параболу, гиперболу и т.п. В итоге приходим к трендовой модели вида:
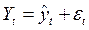 , (55)
, (55)
где 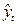 – математическая функция развития;
– математическая функция развития; 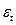 – случайное или циклическое отклонение от функции; t – время в виде номера периода (уровня ряда). Цель такого метода – выбор теоретической зависимости
– случайное или циклическое отклонение от функции; t – время в виде номера периода (уровня ряда). Цель такого метода – выбор теоретической зависимости 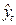 в качестве одной из функций:
в качестве одной из функций:
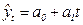 – прямая линия;
– прямая линия; 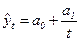 – гипербола;
– гипербола; 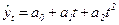 – парабола;
– парабола; 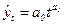 – степенная;
– степенная; 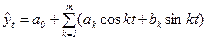 – ряд Фурье.
– ряд Фурье.
.
Определение параметров 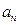 в этих функциях может вестись несколькими способами, но самые незначительные отклонения аналитических (теоретических) уровней (
в этих функциях может вестись несколькими способами, но самые незначительные отклонения аналитических (теоретических) уровней (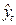 – читается как «игрек, выравненный по t») от фактических (
– читается как «игрек, выравненный по t») от фактических (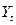 ) дает метод наименьших квадратов – МНК. При этом методе учитываются все эмпирические уровни и должна обеспечиваться минимальная сумма квадратов отклонений эмпирических значений уровней
) дает метод наименьших квадратов – МНК. При этом методе учитываются все эмпирические уровни и должна обеспечиваться минимальная сумма квадратов отклонений эмпирических значений уровней 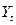 от теоретических уровней
от теоретических уровней 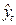 :
:
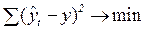 . (56)
. (56)
В нашей задаче при выравнивании по прямой вида 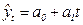 параметры
параметры 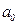 и
и 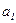 отыскиваются по МНК следующим образом. В формуле (55) вместо
отыскиваются по МНК следующим образом. В формуле (55) вместо 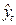 записываем его конкретное выражение
записываем его конкретное выражение 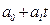 . Тогда
. Тогда 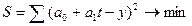 . Дальнейшее решение сводится к задаче на экстремум, т.е. к определению того, при каком значении
. Дальнейшее решение сводится к задаче на экстремум, т.е. к определению того, при каком значении 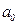 и
и 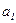 функция двух переменных S может достигнуть минимума. Как известно, для этого надо найти частные производные S по
функция двух переменных S может достигнуть минимума. Как известно, для этого надо найти частные производные S по 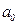 и
и 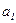 , приравнять их к нулю и после элементарных преобразований решить систему двух уравнений с двумя неизвестными.
, приравнять их к нулю и после элементарных преобразований решить систему двух уравнений с двумя неизвестными.
В соответствии с вышеизложенным найдем частные производные:
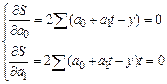
Сократив каждое уравнение на 2, раскрыв скобки и перенеся члены с y в правую сторону, а остальные – оставив в левой, получим систему нормальных уравнений:
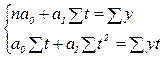 (57)
(57)
где n – количество уровней ряда; t – порядковый номер в условном обозначении периода или момента времени; y – уровни эмпирического ряда.
Эта система и, соответственно, расчет параметров 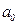 и
и 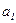 упрощаются, если отсчет времени ведется от середины ряда. Например, при нечетном числе уровней серединная точка (год, месяц) принимается за нуль. Тогда предшествующие периоды обозначаются соответственно –1, –2, –3 и т.д., а следующие за средним (центральным) – соответственно 1, 2, 3 и т.д. При четном числе уровней два серединных момента (периода) времени обозначают –1 и +1, а все последующие и предыдущие, соответственно, через два интервала:
упрощаются, если отсчет времени ведется от середины ряда. Например, при нечетном числе уровней серединная точка (год, месяц) принимается за нуль. Тогда предшествующие периоды обозначаются соответственно –1, –2, –3 и т.д., а следующие за средним (центральным) – соответственно 1, 2, 3 и т.д. При четном числе уровней два серединных момента (периода) времени обозначают –1 и +1, а все последующие и предыдущие, соответственно, через два интервала: 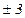 ,
, 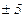 ,
, 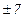 и т.д.
и т.д.
При таком порядке отсчета времени (от середины ряда) 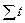 = 0, поэтому, система нормальных уравнений упрощается до следующих двух уравнений, каждое из которых решается самостоятельно:
= 0, поэтому, система нормальных уравнений упрощается до следующих двух уравнений, каждое из которых решается самостоятельно:
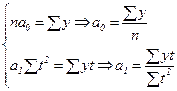 (58)
(58)
Как видим, при такой нумерации периодов параметр 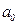 представляет собой средний уровень ряда. Определим по формуле (58) параметры уравнения прямой, для чего исходные данные и все расчеты необходимых сумм представим в таблице 6.
представляет собой средний уровень ряда. Определим по формуле (58) параметры уравнения прямой, для чего исходные данные и все расчеты необходимых сумм представим в таблице 6.
Из таблицы получаем, что 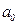 = 12070,2/10 = 1207,02 и
= 12070,2/10 = 1207,02 и 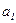 = 4195/330 = 12,7121. Отсюда искомое уравнение тренда
= 4195/330 = 12,7121. Отсюда искомое уравнение тренда 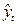 =1207,02+12,7121t. В 6-м столбце таблицы 6 приведены трендовые уровни, рассчитанные по этому уравнению
=1207,02+12,7121t. В 6-м столбце таблицы 6 приведены трендовые уровни, рассчитанные по этому уравнению
По полученной модели для каждого периода (каждой даты) определяются теоретические уровни тренда (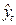 ) и оценивается надежность (адекватность) выбранной модели тренда. Оценку надежности проводят с помощью критерия Фишера, сравнивая его расчетное значение Fр с теоретическими значениями FТ (приложение 1). При этом расчетный критерий Фишера определяется по формуле:
) и оценивается надежность (адекватность) выбранной модели тренда. Оценку надежности проводят с помощью критерия Фишера, сравнивая его расчетное значение Fр с теоретическими значениями FТ (приложение 1). При этом расчетный критерий Фишера определяется по формуле:
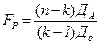 , (59)
, (59)
где k – число параметров (членов) выбранного уравнения тренда; ДА – аналитическая дисперсия, определяемая по формуле (61); До – остаточная дисперсия (62), определяемая как разность фактической дисперсии ДФ (60) и аналитической дисперсии:
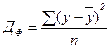 ; (60)
; (60)
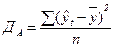 ; (61)
; (61)
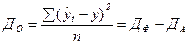 . (62)
. (62)
Сравнение расчетного и теоретического значений критерия Фишера ведется обычно при уровне значимости 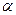 с учетом степеней свободы
с учетом степеней свободы 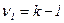 и
и 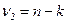 . Уровень значимости
. Уровень значимости 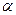 связан с вероятностью
связан с вероятностью 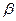 следующей формулой
следующей формулой 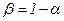 . При условии Fр > FТ считается, что выбранная математическая модель ряда динамики адекватно отражает обнаруженный в нем тренд.
. При условии Fр > FТ считается, что выбранная математическая модель ряда динамики адекватно отражает обнаруженный в нем тренд.
Таблица 6. Вспомогательные расчеты для решения задачи
| Год | y | t | t2 | yt | 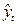
| (y – 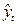 )2 )2
| (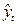 – –  )2 )2
| (y –  )2 )2
|
| 1163,5 | -9 | -10471,5 | 1092,611 | 5025,263 | 13089,44 | 1893,9904 | ||
| 1113,7 | -7 | -7795,9 | 1118,035 | 18,79354 | 7918,3033 | 8708,6224 | ||
| 1100,3 | -5 | -5501,5 | 1143,459 | 1862,733 | 4039,9506 | 11389,1584 | ||
| 1094,1 | -3 | -3282,3 | 1168,884 | 5592,592 | 1454,3822 | 12750,9264 | ||
| 1187,8 | -1 | -1187,8 | 1194,308 | 42,35249 | 161,59803 | 369,4084 | ||
| 1231,4 | 1231,4 | 1219,732 | 136,1394 | 161,59803 | 594,3844 | |||
| 1253,1 | 3759,3 | 1245,156 | 63,10136 | 1454,3822 | 2123,3664 | |||
| 1308,1 | 6540,5 | 1270,581 | 1407,705 | 4039,9506 | 10217,1664 | |||
| 1330,5 | 9313,5 | 1296,005 | 1189,915 | 7918,3033 | 15247,3104 | |||
| 1287,7 | 11589,3 | 1321,429 | 1137,652 | 13089,44 | 6509,2624 | |||
| Итого | 12070,2 | 12070,2 | 16476,25 | 53327,348 | 69803,596 |
Проверим тренд в нашей задаче на адекватность по формуле (59), для чего в 7-м столбце таблицы 6 рассчитан числитель остаточной дисперсии, а в 8-м столбце – числитель аналитической дисперсии. В формуле (59) можно использовать их числители, так как оба они делятся на число уровней n (n сократятся): FР = 53327,348*8/(16476,25*1) = 25,893 > FТ, значит, модель адекватна и ее можно использовать для прогнозирования (FТ = 5,32 находим по приложению 1 в 1-ом столбце [ 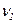 = k – 1 = 1] и 8-й строке [
= k – 1 = 1] и 8-й строке [ 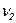 = n – k = 8]).
= n – k = 8]).
При составлении прогнозов уровней социально-экономических явлений обычно оперируют не точечной, а интервальной оценкой, рассчитывая так называемые доверительные интервалы прогноза. Границы интервалов определяются по формуле (63):
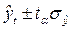 , (63)
, (63)
где 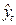 – точечный прогноз, рассчитанный по модели тренда;
– точечный прогноз, рассчитанный по модели тренда; 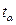 – коэффициент доверия по распределению Стьюдента при уровне значимости
– коэффициент доверия по распределению Стьюдента при уровне значимости 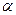 и числе степеней свободы
и числе степеней свободы 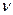 =n–1 (приложение 2);
=n–1 (приложение 2); 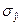 – ошибка аппроксимации, определяемая по формуле (64):
– ошибка аппроксимации, определяемая по формуле (64):
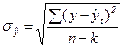 , (64)
, (64)
где 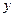 и
и 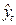 – соответственно фактические и теоретические (трендовые) значения уровней ряда динамики; n – число уровней ряда; k – число параметров (членов) в уравнении тренда.
– соответственно фактические и теоретические (трендовые) значения уровней ряда динамики; n – число уровней ряда; k – число параметров (членов) в уравнении тренда.
Определим доверительный интервал в нашей задаче на 2005 год с уровнем значимости 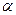 = (1–0,95) = 0,05. Для этого найдем ошибку аппроксимации по формуле (64):
= (1–0,95) = 0,05. Для этого найдем ошибку аппроксимации по формуле (64): 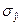 =
= 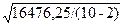 = 45,38. Коэффициент доверия по распределению Стьюдента
= 45,38. Коэффициент доверия по распределению Стьюдента 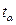 = 2,2622 при
= 2,2622 при 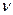 = 10 – 1=9.
= 10 – 1=9.
Прогноз на 2005 с вероятностью 95% осуществим по формуле (63):
Y2005 =(1207,02+12,7121*11) 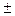 2,2622*45,38 или 1244,19< Y2005 <1449,51 (тыс.чел.).
2,2622*45,38 или 1244,19< Y2005 <1449,51 (тыс.чел.).
Самостоятельные задания по теме
По статистическим данным по России за…гг вычислить: абсолютные, относительные, средние изменения и их темпы базисным и цепным способами. Проверить ряд на наличие в нем линейного тренда, на основе которого рассчитать интервальный прогноз на 2006 год с вероятностью 95%.
| Год | Вариант | |||||||||
| Валовой сбор сахарной свеклы, млн.т. | Валовой сбор картофеля, млн.т. | Число заключенных браков, тыс. | Число построенных жилых домов, млн.м2 | Поголовье крупного рогатого скота, млн.голов (на конец года) | Производство мяса, млн.т. | Производство яиц, млрд.шт. | Численность населения, тыс.чел. (на начало года) | Среднегодовая численность занятых в экономике, тыс.чел. | Доля расходов на оплату ЖКХ в бюджете домохозяйств, % | |
| 14,1 | 897,3 | 30,3 | 16,5 | 4,4 | 34,1 | 4,6 | ||||
| 14,6 | 1001,6 | 31,7 | 15,8 | 4,5 | 35,2 | 5,2 | ||||
| 15,7 | 32,9 | 1019,8 | 33,8 | 15,0 | 4,7 | 36,3 | 6,2 | |||
| 19,4 | 36,7 | 1091,8 | 36,4 | 13,5 | 4,9 | 36,5 | 7,2 | |||
| 21,8 | 35,9 | 979,7 | 41,0 | 12,1 | 5,0 | 35,8 | 7,7 | |||
| 21,4 | 37,3 | 1066,4 | 43,6 | 11,1 | 4,9 | 36,8 | 8,3 |
Тема 5. Индексы
Методические указания по теме
Задача 1. Имеются следующие данные о продажах торговой точкой двух видов товара:
| Товар | Цена за кг, руб. | Объем продаж, тыс. кг | ||
| Январь | Февраль | Январь | Февраль | |
| Апельсины | ||||
| Бананы |
Определить: 1) индивидуальные индексы цен, физического объема и выручки; 2) общие индексы цен, физического объема и выручки; 3) абсолютное изменение выручки за счет изменений цен, структурного сдвига и объемов продаж (для каждого фактора в отдельности) по всей продукции и по каждому товару в отдельности. По итогам расчетов сделать аргументированные выводы.
Решение. В основе решения задачи лежит формула (65):
Q=p×q, (65)
где p – цена товара, q – физический объем (количество), Q – выручка (товарооборот).
Применив формулу (65) к нашей задаче, рассчитаем выручку по каждому товару в январе (Q0j) и феврале (Q1j) в таблице 7.
Таблица 7. Расчет выручки и ее изменения по каждому товару
| Товар j | Январь Q0j | Февраль Q1j | Изменение выручки ∆Qj= Q1j– Q0j |
| Апельсины | 20*100 = 2000 | 18*160 = 2880 | |
| Бананы | 22*150 = 3300 | 25*120 = 3000 | -300 |
| Итого |
Из таблицы видно, что абсолютное изменение общей выручки составило:
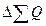 = ∑Q1–∑Q0 = 5880-5300 = 580 тыс. руб., то есть она выросла на 580 тыс. руб.
= ∑Q1–∑Q0 = 5880-5300 = 580 тыс. руб., то есть она выросла на 580 тыс. руб.
Общий индекс изменения выручки равняется:
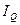 = ∑Q1/∑Q0 = 5880/5300 = 1,1094, то есть выручка от продажи фруктов увеличилась в 1,1094 раза или на 10,94% в феврале по сравнению с январем.
= ∑Q1/∑Q0 = 5880/5300 = 1,1094, то есть выручка от продажи фруктов увеличилась в 1,1094 раза или на 10,94% в феврале по сравнению с январем.
Определим индивидуальные индексы цен (ip), физического объема (iq), выручки (iQ) и доли товара (id) по формуле (2), используя в качестве Xi цены (p), физический объем (q), выручки (Q) и доли товара (d=q/∑q) каждого вида фруктов соответственно. Результаты расчетов представим в таблице 8.
Таблица 8. Расчет индивидуальных индексов
| Индивидуальный индекс | апельсины | бананы |
| количества iq | 160/100 = 1,6 | 120/150 = 0,8 |
| отпускных цен ip | 18/20 = 0,9 | 25/22 = 1,136 |
| выручки iQ | 2880/2000=1,44 | 3000/3300=0,909 |
| доли товара id | (160/280)/(100/250) = 1,429 | (120/280)/(150/250) = 0,714 |
Правильность выполненных расчетов проверяется следующим образом:
1) общее изменение выручки должно равняться сумме ее частных (по каждому товару в отдельности) изменений: 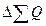 = 880+(-300) = 580 (тыс. руб.);
= 880+(-300) = 580 (тыс. руб.);
2) произведение факторных индивидуальных индексов по периодам должно равняться соответствующему индивидуальному индексу выручки: iQ А=1,6*0,9 =1,44; iQ Б= 0,8*1,136 = 0,909.
Из таблицы видно, что в феврале по сравнению с январем:
– количество проданных апельсинов увеличилось в 1,6 раза или на 60%, а бананов – уменьшилось в 0,8 раза или на 20%;
– цена апельсинов понизилась в 0,9 раза или на 10%, а бананов – повысилась в 1,136 раза или на 13,6%;
– выручка по апельсинам выросла в 1,44 раза или на 44%, а по бананам – снизилась в 0,909 раза или на 9,1%;
– доля проданных апельсинов увеличилась в 1,429 раза или на 42,9%, а бананов – уменьшилась в 0,714 раза или на 28,6%.
Агрегатный общий индекс физического объема Ласпейреса определяется по формуле (66):
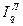 =
= 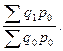 (66)
(66)
В нашей задаче 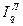 =
= 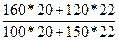 = 5840/5300 = 1,10189, то есть количество проданных фруктов в базисных (январских) ценах выросло в 1,10189 раза или на 10,189% в феврале по сравнению с январем.
= 5840/5300 = 1,10189, то есть количество проданных фруктов в базисных (январских) ценах выросло в 1,10189 раза или на 10,189% в феврале по сравнению с январем.
Агрегатный общий индекс цен Пааше рассчитывается по формуле (67):
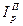 =
= 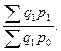 (67)
(67)
В нашей задаче 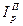 =
= 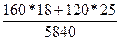 = 5880/5840 = 1,00685, то есть цена проданных фруктов при объемах продаж отчетного (февральского) периода выросла в 1,00685 раза или на 0,685% в феврале по сравнению с январем.
= 5880/5840 = 1,00685, то есть цена проданных фруктов при объемах продаж отчетного (февральского) периода выросла в 1,00685 раза или на 0,685% в феврале по сравнению с январем.
Контрольосуществляется по формуле: IQ = 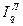
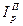 = 1,10189*1,00685 = 1,1094.
= 1,10189*1,00685 = 1,1094.
Агрегатный общий индекс цен Ласпейреса вычисляется по формуле (68):
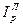 =
= 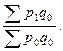 (68)
(68)
В нашей задаче 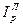 =
= 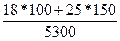 = 5550/5300 = 1,04717, то есть цена проданных фруктов при объемах продаж базисного (январского) периода выросла в 1,04717 раза или на 4,717% в феврале по сравнению с январем.
= 5550/5300 = 1,04717, то есть цена проданных фруктов при объемах продаж базисного (январского) периода выросла в 1,04717 раза или на 4,717% в феврале по сравнению с январем.
Агрегатный общий количественный индекс Пааше рассчитывается по формуле (69):
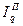 =
= 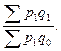 (69)
(69)
В нашей задаче 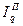 = 5880/5550 =1,05946, то есть количество проданных фруктов в отчетных (февральских) ценах выросло в 1,05946 раза или на 5,946% в феврале по сравнению с январем.
= 5880/5550 =1,05946, то есть количество проданных фруктов в отчетных (февральских) ценах выросло в 1,05946 раза или на 5,946% в феврале по сравнению с январем.
Контроль осуществляется по формуле: IQ = 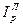
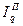 = 1,04717*1,05946 =1,1094.
= 1,04717*1,05946 =1,1094.
Средняя геометрическая величина определяется из индексов Ласпейреса и Пааше (по методике Фишера) по формуле (70) для количества товаров и по формуле (71) – для цен:
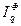 =
= 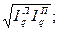 (70)
(70) 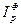 =
= 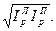 (71)
(71)
В нашей задаче 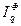 =
= 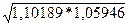 =1,0805, то есть в среднем количество проданных фруктов выросло в 1,0805 раза или на 8,05%;
=1,0805, то есть в среднем количество проданных фруктов выросло в 1,0805 раза или на 8,05%; 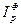 =
= 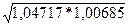 =1,0268, то есть в среднем цена проданных фруктов выросла в 1,0268 раза или на 2,68%.
=1,0268, то есть в среднем цена проданных фруктов выросла в 1,0268 раза или на 2,68%.
Далее выполняется факторный анализ общей выручки. В его основе лежит следующая трехфакторная мультипликативная модель выручки:
IQ = 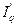
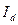
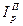 , (72)
, (72)
где 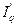 =
= 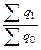 ,
, 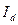 – индекс структурных сдвигов, показывающий как изменилась выручка под влиянием фактора изменения долей проданных фруктов в отчетном периоде по сравнению с базисным периодом. Он определяется по формуле (73):
– индекс структурных сдвигов, показывающий как изменилась выручка под влиянием фактора изменения долей проданных фруктов в отчетном периоде по сравнению с базисным периодом. Он определяется по формуле (73):
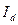 =
= 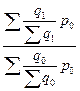 =
= 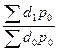 . (73)
. (73)
В нашей задаче 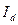 =
= 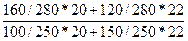 = 0,9838, то есть структурный сдвиг должен был уменьшить отчетную выручку в базисных ценах в 0,9838 раза или на 1,62%.
= 0,9838, то есть структурный сдвиг должен был уменьшить отчетную выручку в базисных ценах в 0,9838 раза или на 1,62%.
Тогда изменение выручки за счет изменения общего количества фруктов определяется по формуле (74):
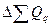 =
= 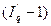
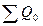 . (74)
. (74)
В нашей задаче 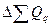 = (1,12-1)*5300 = 636 (тыс. руб.), то есть изменение количества проданных фруктов увеличило выручку на 636 тыс. руб.
= (1,12-1)*5300 = 636 (тыс. руб.), то есть изменение количества проданных фруктов увеличило выручку на 636 тыс. руб.
Изменение общей выручки за счет структурных сдвигов находится по формуле (75):
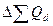 =
= 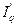
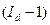
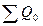 . (75)
. (75)
В нашей задаче 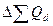 = 1,12*(0,9838-1)*5300 = –96 (тыс. руб.), то есть структурный сдвиг в количестве проданных фруктов уменьшил выручку на 96 тыс. руб.
= 1,12*(0,9838-1)*5300 = –96 (тыс. руб.), то есть структурный сдвиг в количестве проданных фруктов уменьшил выручку на 96 тыс. руб.
Изменение общей выручки за счет изменения отпускных цен рассчитывается по формуле (76):
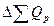 =
= 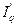
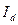
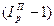
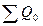 . (76)
. (76)
В нашей задаче 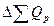 =1,12*0,9838*(1,00685-1)*5300 = 40 (тыс. руб.), то есть изменение цен на фрукты увеличило выручку на 40 тыс. руб.
=1,12*0,9838*(1,00685-1)*5300 = 40 (тыс. руб.), то есть изменение цен на фрукты увеличило выручку на 40 тыс. руб.
Контроль правильности расчетов производится по формуле (77), согласно которой общее изменение выручки равно сумме ее изменений за счет каждого фактора в отдельности.
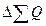 =
= 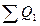 -
- 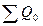 =
= 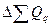 +
+ 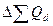 +
+ 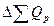 . (77)
. (77)
|
|
|
|
|
Дата добавления: 2014-12-24; Просмотров: 845; Нарушение авторских прав?; Мы поможем в написании вашей работы!