Второе начало термодинамики (устанавливает определённое направление течения процессов в природе – стрела времени)

Первая часть: Каждая термодинамическая система обладает функцией состояния, называемой энтропией (энтропия – изменение). Энтропия вычисляется следующим образом. Система переводится из произвольно выбранного начального состояния через последовательность состояний равновесия, вычисляются все подводимые при этом к системе порции тепла 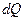, делится каждая на соответствующую ей абсолютную температуру 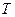, и все полученные таким образом значения суммируются.

Вторая часть: При реальных (неидеальных) процессах энтропия изолированной системы возрастает .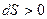

Если обозначить энтропию через , то

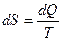(2)

и получим соотношение Гиббса:

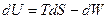(3)

Это фундаментальное уравнение, объединяющее первое и второе начала, и в нём по существу заключена вся равновесная термодинамика.

Второе начало термодинамики позволяет судить о направлении процесса и имеет различные формулировки.

Томсона: «Невозможно построить периодически действующую машину, единственным результатом которой было бы поднятие груза за счёт охлаждения теплового резервуара».

Клаузиуса: «Теплота не может самопроизвольно переходить от тела менее нагретого к телу более нагретому».

Из второго постулата следует:

- существование энтропии как функции состояния системы;

- принцип возрастания энтропии.

В гигантской фабрике естественных процессов принцип энтропии занимает место директора, который предписывает вид и течение всех сделок. Закон сохранения энергии играет лишь роль бухгалтера, который приводит в равновесие дебет и кредит.

Третье начало термодинамики (тепловая теорема Нернста)

При абсолютном нуле температуры энтропия принимает значение 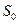, не зависящее от давления, агрегатного состояния и других характеристик вещества. Эту величину можно положить равной рулю.

Теорема Нернста не вытекает из первых двух начал, поэтому в силу своей общности может рассматриваться как новый закон природы - третье начало термодинамики.

В отличие от нулевого, первого и второго начал теоремы Нернста не вводит в термодинамику новой функции состояния, однако именно она делает функции состояния численно определёнными и практически полезными.

Содержание тепловой теоремы Нернста сводится к двум утверждениям.

Первое утверждение состоит в том, что при приближении к абсолютному нулю энтропия стремится к определённому конечному пределу. Поэтому имеет смысл говорить об энтропии тела при абсолютном нуле температур. То есть интеграл

сходится.

Вторая часть теоремы Нернста утверждает, что все процессы при абсолютном нуле температур, переводящие систему из одного равновесного состояния в другое равновесное состояние, происходят без изменения энтропии.

В 1906 году немецкий физикохимик В.Г.Нернст сформулировал свою знаменитую тепловую теорему, ставшую третьим началом термодинамики. Тем самым было завершено аксиоматическое построение классической термодинамики.

Этот этап термодинамики сыграл выдающуюся роль в истории науки.

Логическая стройность равновесной термодинамики, основанной на четырёх началах, породила мнение, что термодинамика уже доведена до своего окончательного завершения. Эту точку зрения целиком поддерживал Нернст, считавший, что развитие термодинамики закончилось.

Такой взгляд не выдержал испытания временем. История науки свидетельствует, что всякая глубокая научная идея не может быть исчерпана до конца. Более того, сама идея развивается и обогащается по мере углубления наших знаний. Именно так обстоит дело с термодинамикой.

Теорема Нернста подвела итог развитию классической равновесной термодинамики.

Классическая термодинамика – это область физики, которая занимается изучением общих свойств макроскопических систем в равновесии, а также общих закономерностей при установлении равновесия.

Из всего многообразия макроскопических объектов, которые нас окружают или которые мы используем в повседневной жизни или работе, термодинамика изучает объекты только в состоянии термодинамического равновесия.

Под состоянием термодинамического равновесия подразумевается состояние, в которое с течением времени рано или поздно приходит система, находящаяся при определённых внешних условиях и определённой постоянной температуре окружающих тел.

При достижении термодинамического равновесия система забывает свою предысторию.

Она помнит только то, что сохраняется в силу законов сохранения (в изолированной системе это суммарные энергия, импульс и масса).

С этой точки зрения окружающий нас мир: мир животных, мир растений, мир неживой природы – представляют собой системы, не находящиеся в состоянии термодинамического равновесия.

Термодинамическое равновесие есть некая абстракция. По отношению к окружающему нас миру это упрощённая модель. Тем не менее, в огромном большинстве практически важных случаев она приводит к правильным результатам.

Термодинамика, как уже говорилось, изучает свойства равновесных состояний. А для равновесных состояний понятия времени не существует. Поэтому время в явном виде в термодинамику не входит (термодинамика не знает времени). В этом смысле об обычной термодинамике говорят как о термостатике (термин введён в 1854 г. В.Томсоном взамен «механической теории тепла»).

Термодинамика позволяет также сделать выводы об общих закономерностях процессов, происходящих при установлении равновесия. Эти выводы касаются направления необратимых процессов и их возможностей при данных условиях. Однако все выводы классической равновесной термодинамики о неравновесных процессах или неравновесных состояниях по-прежнему не включают времени. Утверждение о направлении процесса или запрета процесса не даёт никакой информации о скорости процесса.

Классический этап развития термодинамики кроме формулировки основных начал и анализа вытекающих из них следствий оставил нам в наследство программу действий, связанную прежде всего с необходимостью описания неравновесных процессов.

Классическая термодинамика является мощным средством исследования обратимых процессов. Могущество термодинамического метода состоит в том, что он позволяет получить основные закономерности квазистатических процессов, не вскрывая их молекулярного механизма.

Вполне естественно возникает идея о необходимости создания аналогичного метода для исследования необратимых процессов. В настоящее время такой метод создан и получил своё окончательное оформление под названием термодинамики необратимых процессов.

Сегодня закончена разработка основ линейной теории неравновесных процессов, завершившейся созданием линейной неравновесной термодинамики.

Одно из направлений завтрашнего дня - создание нелинейной феноменологической теории неравновесных процессов.

Термодинамика неравновесных необратимых процессов – это физическая теория макроскопического описания неравновесных процессов.

Закрепление материала (другой взгляд). Превращение вещества. Взаимосвязь термодинамики и кинетики.

В связи с химическими и физическими преобразованиями материи возникает два вопроса:

1) Могут – ли эти преобразования происходить?

2) Как быстро они происходят?

Ответ на первый вопрос – предмет рассмотрения термодинамики. Операции с термодинамическими функциями, характеризующими вещество, позволяют ответить на вопрос о принципиальной возможности или невозможности тех или иных превращений веществ в заданных условиях, а также о возможности преобразования энергии. Это главные вопросы в энергетике и технологии производства материалов. Выводы делаются на основании трёх законов термодинамики.

Первый закон утверждает, что энергия не может быть ни создана, ни уничтожена. При любом изменении общее количество энергии сохраняется.

Второй закон дополняет это утверждение. В нём вводится ещё одно свойство системы – энтропия, которая используется в качестве критерия для выяснения вопроса, имеет ли термодинамическая система естественную тенденцию к данному преобразованию.

Третий закон даёт возможность рассчитать энтропию системы на основании знания распределения молекул, составляющих систему, по доступным энергетическим уровням. Он устанавливает связь между идеями квантовой теории и термодинамикой и утверждает, что при Т→0 энтропии разных совершенных кристаллов стремятся к одному и тому же значению.

Химическая термодинамика имеет дело с термодинамическими системами, в которых может меняться число частиц или их состав. Это самый сложный раздел термодинамики с особым математическим аппаратом, основанным на понятиях химического потенциала и константы равновесия.

Химическая кинетика отвечает на вопрос – как скоро произойдёт нужное превращение в заданных условиях, если оно разрешено термодинамикой. Главная величина в кинетике, характеризующая скорость превращения – константа скорости реакции. Изобразим превращение веществ в виде

,

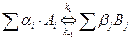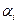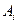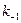где , – стехиометрические коэффициенты, , – символы веществ, , – константы скорости прямой и обратной реакции соответственно. В состоянии равновесия фундаментальную связь между термодинамикой (константа равновесия 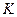) и кинетикой (константа скорости ) устанавливает закон Вант-Гоффа:

.

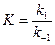Термодинамическая система.

Определим термодинамическую систему как совокупность взаимодействующих друг с другом тел, способных обмениваться с окружением энергией и веществом.

Если система состоит из отдельных частей, разграниченных поверхностями и обладающих различными свойствами, то она называется гетерогеннойсистемой. Такую систему можно назвать многофазной. При отсутствии разграничивающих поверхностей между любыми частями системы она называется гомогеннойсистемой. Если же во всех частях системы её свойства одинаковы, то такая гомогенная система называется однородной.

Часть гетерогенной системы, разграниченная от других частей поверхностью раздела и имеющая во всех своих точках одинаковые физические свойства и состав называется фазой.

Системы делятся по их способности взаимодействовать с окружением в смысле обмена энергией Е и массой вещества m.

Изолированная система− система, которая не обменивается с окружением ни энергией, ни веществом, т. е. δΕ = 0, δm = 0.

Открытая система− система, которая может обмениваться энергией и веществом с окружением, т. е δΕ ≠ 0, δm ≠ 0.

Закрытая системане обменивается с окружением веществом, но обмен энергией с окружением возможен, т. е. δΕ ≠ 0, δm = 0.

В адиабатической системеотсутствует теплообмен с окружением т. е. δQ = 0, где Q – тепло.

Квазизамкнутая подсистема− произвольно выделенная любая часть термодинамической системы, собственная энергия которой много больше, чем энергия её взаимодействия с остальной частью системы. Такую подсистему образуют, например, молекулы однородной жидкости, заключённые внутри сферы с центром в произвольной точке этой жидкости и радиусом R. Величина R много больше, чем радиус действия межмолекулярных сил r. Число молекул, расположенных внутри выделенной сферы N ~ R³, будет много больше числа молекул n, расположенных на её поверхности в слое r, причём n ~ R²⋅r. Поэтому суммарная внутренняя энергия всех молекул внутри сферы будет много больше суммарной энергии взаимодействия молекул, расположенных на её поверхности, с ближайшими к ним молекулами, расположенными вне сферы.

Параметры состояния.

Набор величин, характеризующих состояние системы, называют термодинамическими параметрами. Чаще всего в их качестве используются давление – Р, температура – Т, объём – V, концентрация – С.

Параметры, пропорциональные массе системы называют экстенсивными.Например, энергия и объём системы при постоянной плотности. Экстенсивный параметр Ф системы равен сумме параметров Ф_i, характеризующих отдельные части системы.

Интенсивные параметры от величины системы не зависят, например температура, давление, концентрация, напряжённость внешних полей, удельная теплоёмкость, и др. Система может находиться в равновесном или неравновесном состоянии.

Равновесное состояние– состояние термодинамической системы, которое в отсутствие внешних воздействий не меняется со временем при бесконечно долгом наблюдении за ней. В молекулярных системах равновесие имеет динамический характер. В условиях равновесия каждому процессу, протекающему в системе, соответствует обратный процесс, идущий с той же скоростью.

Под термодинамическим процессомпонимается любое изменение состояния системы, фиксируемое по изменению одного или нескольких термодинамических параметров.

Если начальное состояние было равновесным, то процесс в системе возможен только при изменении внешних условий. Термодинамический процесс называется квазистатическимили равновесным,если внешние условия меняются столь медленно, что в любой момент времени систему можно рассматривать как равновесную. Термодинамический процесс называется обратимым, если при его проведении сначала в прямом, а затем в обратном направлении не остаётся никаких изменений ни в системе, ни в окружении. Равновесный процесс всегда обратим, а обратимый процесс всегда идёт через непрерывный ряд равновесных состояний системы.

Всякое физическое тело (система), поставленное в определённые внешние условия, рано или поздно приходит в состояние термодинамического (статистического) равновесия.

Внешние условия характеризуются своими параметрами.

Наше тело (система) – внутренними параметрами. Эти параметры характеризуют свойства самой системы.

Внутренние параметры зависят от внешних параметров.

В состоянии термодинамического равновесия системы они имеют при заданных внешних параметрах и температуре (энергии) определённые численные значения.

Одна и та же величина, в зависимости от условий, в которых находится система, может играть роль как внешнего, так и внутреннего параметра.

Например. Если фиксировано положение стенок сосуда, объём является внешним параметром, а давление – внутренним. Если, однако, ограничить систему в сосуде подвижным поршнем под постоянной нагрузкой, то давление будет внешним параметром, а объём – внутренним параметром.

Итак, интуитивно считается очевидным, что если изолированную систему оставить в покое, то она в конце концов придёт в равновесие. Но каким образом это будет происходить – большой вопрос.

Если система поставлена в определённые внешние условия (то есть, заданы её внешние параметры), но она находится в неравновесном состоянии (то есть, её внутренние параметры не имеют равновесных значений), то система изменяется во времени, приближаясь к своему равновесному состоянию.

Процесс перехода термодинамической системы из неравновесного состояния в равновесное называется процессом релаксации. При этом для выравнивания значения каждого параметра по всему объёму системы существует свое характерное время релаксации – время релаксации для данного параметра. Роль полного времени релаксации играет, очевидно, максимальное из этих времён. Более подробно об этом мы поговорим когда будем изучать принципы неравновесной термодинамики.

Уравнение состояния идеального газа. Свойства идеального газа.

Идеальный газ – математическая модель газа, в котором в рамках молекулярно кинетической теории газа предполагается, что:

1 – потенциальной энергией взаимодействия молекул можно пренебречь;

2 – суммарный объём молекул газа пренебрежимо мал;

3 – между молекулами не действуют силы притяжения и отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги;

4 – время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.

При высоких температурах система близка к идеальному газу. Действительно, температура характеризует среднюю кинетическую энергию молекул: 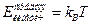( 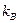- постоянная Больцмана). Соответственно, при повышении температуры кинетическая энергия молекул растет и, в конечном счете, окажется много больше характерной энергии их взаимодействия. Но это и есть условие того, что система представляет собой идеальный газ. Уравнение состояния идеального газа получается из молекулярно кинетической теории путём подсчёта суммарного изменения количества движения молекул в результате соударения со стенкой. Уравнение состояния идеального газа имеет вид.

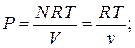
- полное число молей в газе; 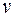- объем одного моля; 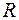- универсальная газовая постоянная. Соответственно, зависимость давления от объема при этих температурах близка к гиперболе.

Теплоемкость, энтальпия, энтропия идеальных газов

Дата добавления: 2014-12-24