ТЕМА 6. Измерение связи между явлениями. Методы изучения Корреляционных связей при оценке показателей здоровья и факторов окружающей среды

ЦЕЛЬ ЗАНЯТИЯ: Освоить принципы измерения корреляционной связи и овладеть методикой измерения связи между явлениями.

Методика проведения занятия: Студенты самостоятельно готовятся к практическому занятию по рекомендованной литературе и выполняют индивидуальное домашнее задание. Преподаватель в течение 10 минут проверяет правильность выполнения домашнего задания и указывает на допущенные ошибки, проверяет степень подготовки с использованием тестирования и устного опроса. Затем студенты самостоятельно вычисляют коэффициенты корреляции по способу квадратов (Пирсона) и по способу рангов (Спирмена); проводят оценки достоверности коэффициента корреляции. Оценивают полученные данные и формулируют заключение. В конце занятия преподаватель проверяет самостоятельную работу студентов.

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1. Какие виды связи существуют между явлениями или признаками?

2. Является ли функциональная связь характерной для медико-биологических явлений?

3. Что такое корреляционная связь?

4. Можно ли считать, что при корреляционной связи значению одного признака соответствует несколько значений другого, взаимосвязанного с ним признака?

5. Можно ли утверждать, что корреляционная связь проявляется в массе наблюдений, т.е. в совокупности?

6. Что является критерием оценки характера и силы корреляции?

7. Можно ли утверждать, что коэффициент корреляции дает представление о наличии и направлении корреляционной связи?

8. С повышением температуры тела увеличивается частота пульса у большинства больных. Можно ли утверждать, что такая взаимосвязь относится к прямой корреляции?

9. Можно ли утверждать, что диапазон значений коэффициента корреляции находится в пределах от -1 до +1?

10. Каковы методы определения коэффициента корреляции?

11. Можно ли утверждать, что метод квадратов (Пирсона) дает более точные результаты по сравнению с методом рангов (Спирмена)?

12. Каков порядок определения коэффициента корреляции по методу рангов?

13. Как определяется характер и сила связи по коэффициенту корреляции?

14. Как оценивается достоверность коэффициента корреляции?

15. Можно ли утверждать, что если коэффициент корреляции более чем в три раза превышает свою ошибку, то он достоверен?

КРАТКОЕ СОДЕРЖАНИЕ ТЕМЫ:

Задача каждой науки – вскрыть и изучить наиболее существенные связи между явлениями и процессами. Известны два вида связи между явлениями (признаками): функциональная и корреляционная. Функциональная связь отражает строгую зависимость процессов или явлений и изменение какого-либо одного явления обязательно связано с изменением числовых значений другого явления на строго определенную величину. Функциональная связь, как правило, проявляется при физических и химических явлениях, где её можно представить в виде уравнения, формулы. Примеров функциональной связи может являться увеличение объема шара в строгой зависимости от увеличения его радиуса, расширение тела по мере увеличения температуры нагревания и т.д. Корреляция – понятие, которое также означает взаимосвязь между признаками. При корреляционных связях, характерных для медико-биологических явлений, значению одного признака соответствуют разные значения других признаков. Корреляционная связь необходима, например, при оценке взаимосвязей между стажем работы и уровнем заболеваемости работающих; между разными уровнями физических факторов окружающей среды и состоянием здоровья; между различными уровнями интенсивности нагрузки и частотой (уровнем) физиологических реакций организма; между сроками госпитализации и частотой осложнений. Статистика позволяет исследователю измерить связи, обосновать выводы и наглядно их иллюстрировать. Корреляционная связь бывает положительной - прямой (при увеличении одного признака увеличивается другой) и отрицательной - обратной (при увеличении одного показателя другой уменьшается). Коэффициент корреляции свидетельствует не только о направлении связи, но и об уровне этой связи. Сильная связь выражается коэффициентом от 0,7 до 0,99, средняя — от 0,3 до 0,69, слабая — до 0,29. При нулевом значении коэффициента связи отсутствуют.

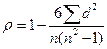Наиболее простыми методом определения коэффициента корреляции являются ранговая корреляция: , где 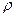- коэффициент ранговой корреляции, d - разность рангов, n –число сопоставляемых пар признаков.При ранговой корреляции числовые выражения сравниваемых статистических рядов ранжируют, то есть проставляют ранговые номера для каждой цифры (от 1 и далее) и подставляют значения в формулу с учетом разницы порядковых значений. При расчете коэффициента корреляции методом квадратов (метод Пирсона) сначала вычисляют среднее значение в каждом вариационном ряду сравниваемых групп. Затем находят отклонение каждой величины ряда от полученной средней. Для устранения отрицательных значений эти величины возводят в квадрат и подставляют в формулу: r_{xy =} , где d_x и d_y – отклонение каждой варианты от своей средней арифметической М_х и М_y. По величине коэффициента устанавливают направление и силу связи. Достоверность коэффициента определяют по таблицам критических значений (таблицам Каминского) при n’ = n-2 (приложение, табл. 4), а также при расчете средней ошибки и критерия достоверности t. Коэффициент корреляции должен превышать свою ошибку не менее чем в 3 раза. Формула ошибки коэффициента ранговой корреляции: m = 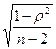, t = 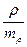По методу Пирсона ошибка коэффициента корреляции вычисляется по формуле: m_{r =} , t = . Значения t оценивается по таблице критических значений критерия t (при n<30, приложение, табл. 2).

ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ:

ЗАДАНИЕ 1: Вычислить коэффициент ранговой корреляции, определить направление и силу корреляционной связи, оценить достоверность полученных данных

Задача 1.

Существует ли связь между стажем работы на машиностроительном предприятии и показателями заболеваемости рабочих?

Стаж работы	До 1 года	1-3 года	4-5 лет	6-10 лет	11-15 лет	16-20 лет	21-25 лет	26 и более
Число случаев заболеваний на 100 рабочих	59,6	41,9	40,8	64,7	64,7	77,5	83,6	112,8

Задача 2.

Существует ли связь между возрастом заболевших гриппом и уровнем смертности от этого заболевания?

Возраст заболевших в годах	До 1 года	1-4	5-9	10-14	15-17	18-20	21-30	31-40	41-50	51-60	61 и старше
Смертность на 100000 человек	68,3	57,7	55,9	24,7	55,9	42,1	67,9	86,6	89,4	106,7	158,2

Задача 3.

Существует ли связь между возрастом мужчин и уровнем смертности

Возраст в годах	0-4	5-9	10-14	15-24	25-34	35-44	45-54	55-64	65 и старше
Уровень смертности на 100000 человек	801,0	272,0	194,7	296,8	624,1	922,8	2624,4	4324,5	9275,1

Задача 4.

Существует ли связь между долей контингента часто болеющих (ЧБ) и возрастом детей

Возраст в годах	До 1 года	1-2	3-4	5-6	7-8	9-10	11-12	13-14
Доля ЧБ	28,5	48,2	44,9	38,7	38,7	27,9	24,2	20,1

Задача 5.

Существует ли связь между возрастом и частотой нарушения зрения у детей

Возраст в годах	0-3	4-5	6-7	8-9	10-11	12-13	14-15	16-17
Нарушения зрения, ‰	18,9	20,7	31,4	42,7	42,1	54,6	54,6	92,0

Задача 6.

Существует ли связь между порядковым номером месяца года и частотой обращения населения за скорой и неотложной медицинской помощью по поводу сердечно-сосудистых заболеваний

Месяц	январь	февраль	март	апрель	май	июнь	июль	август	сентябрь	октябрь	ноябрь	декабрь
Частота обращений за СНМП ‰	114,3	108,3	109,7	103,2	104,5	95,2	98,4	97,8	87,6	92,7	92,7	96,4

Задача 7.

Существует ли связь между расстоянием от места жительства до предприятия и заболеваемостью рабочих

Расстояние в метрах	До 500 м.	600-1000	1100-3000	3100-4000	4100-5000	5100-7000	7100-9000	9100 и более
Заболеваемость ‰	920,1	887,9	920,1	954,0	1286,3	1107,8	1510,8	1832,7

Задача 8.

Существует ли связь между временем прошедшим от возникновения острого приступа холецистита до начала проведения операции и частотой послеоперационных осложнений

Время в часах	До 3 часов	3-5	6-8	9-11	12-14	15-17	18-20	21-23	24 и более
Частота осложнений в %

Задача 9.

Существует ли связь между возрастной группой и частотой самоубийств у мужчин

Возрастная группа умерших, годы	До 20	20-29	30-39	40-49	50-59	60-69	70 и старше
Частота самоубийств на 100 тыс. чел.	4,1	28,5	43,8	54,8	54,8	48,2	75,5

Задача 10.

Существует ли связь между возрастной группой мужчин и распространенностью психических заболеваний

Возрастная группа, годы	0-4	5-9	10-14	15-19	20-24	25-29	30-39	40-49	50-59	60-69	70 и старше
Заболеваемость ‰	16,2	35,4	31,2	8,1	10,2	35,0	31,4	53,1	58,8	30,5	19,2

Задача 11.

Существует ли связь между возрастом ребенка и количеством больных с эквиноварусной деформацией стоп, обусловленной спастическими парезами в нижних конечностях

Возраст	До 1 месяца	1- 3 месяца	4 – 6 месяцев	7-9 мес.	10-12 мес.	1-2 года	2-3 года	Старше 3 лет
Кол-во больных

Задача 12.

Существует ли связь между возрастной группой и уровнем травматизма у мужчин

Возрастная группа мужчин, годы	Дети от 0 до 14 лет	15-17	18-19	20-29	30-39	40-49	50-59	60-69	70 и старше
Частота травматизма на 100 тыс. чел.	72,3	165,6	233,6	196,9	157,2	176,3	153,3	141,9	97,2

Задача 13.

Существует ли связь между возрастом и уровнем смертности женщин в Российской Федерации

Возраст в годах	До 1 года	1-4	5-9	10-14	15-24	25-34	35-44	45-54	55-64	65 и старше
Уровень смертности на 100000 человек	10,9	0,7	0,3	0,3	0,85	1,8	3,6	7,7	15,4	113,9

Задача 14.

Существует ли связь между возрастной группой пациентов и долей полностью удовлетворенных качеством лечения в стационаре

Возраст в годах	15-20	21-25	26-30	31-35	36-40	41-45	46-50	51-55	56-60	61 и и старше
% удовлетворенных качеством лечения	77,6	81,1	75,2	64,3	64,3	50,1	48,9	46,2	39,9	20,7

ЗАДАНИЕ 2: Вычислить коэффициент корреляции методом квадратов (Пирсона), определить направление и силу корреляционной связи, оценить достоверность полученных данных

Задача 1.

Существует ли связь между долей детей, охваченных прививками против кори, и уровнем заболеваемости корью

Охвачено прививками, %
Заболеваемость на 100 тыс. чел.

Задача 2.

Существует ли связь между ростом и массой тела у студентов-медиков в возрасте до 19 лет

Рост в см.
Масса, кг

Задача 3.

Существует ли связь между стажем работы в цехах с вредными условиями труда и кратностью заболеваемости с временной утратой трудоспособности

Стаж работы (лет)
Кратность случаев ВН (раз)

Задача 4.

Существует ли связь между длиной и массой тела у новорожденных

Длина, см.
Масса, кг	2,4	3,1	4,1	3,6	3,2	3,3	3,5	3,8	3,5	3,8	4,0

Задача 5.

Существует ли связь между количеством бактерий, вырастающих при посеве 0,1 мл. обеззараженной воды и дозой остаточного хлора в 1 мл. воды

Доза остаточного хлора (мг/л)	0,05	0,10	0,07	0,60	2,00	1,00	0,80	1,2	3,00
Число бактерий

Задача 6.

Существует ли связь между возрастом родильницы и количеством грудного молока

Возраст в годах
Лактация в гр.

Задача 7.

Существует ли связь междудлительностью охлаждения организма и уровнем молочной кислоты (мг%)

Дни охлаждения
Уровень молочной кислоты мг%	7,0	7,0	7,2	7,1	8,5	8,9	8,7	8,9	9,0	9,5

Задача 8.

Существует ли связь между возрастом пациентов и потребностью их в медицинской помощи (эквивалентные единицы на 1 чел.)

Возраст в годах
Потребность в мед. помощи	10,0	7,0	2,2	2,0	2,0	3,5	5,0	7,5	10,1	12,0

Задача 9.

Существует ли связь между температурой воздуха осенью и частотой возникновения ОРВИ

t воздуха
Случаи ОРВИ

Задача 10.

Существует ли связь между возрастом и заболеваемостью студентов медицинской академии

Возраст, лет
Заболеваемость на 1000 чел.

Рекомендуемая литература.

· Ю.П. Лисицын. Общественное здоровье и здравоохранение. Учебник для вузов. М., 2002. –с. 303-304.

· Ю.П. Лисицын. Социальная гигиена (медицина) и организация здравоохранения. Казань, 1999. –с. 306-307.

· В.К. Юрьев, Г.И. Куценко. Общественное здоровье и здравоохранение. С.-П., 2000. –с.199-201.

· А.Ф. Серенко, В.В. Ермаков. Социальная гигиена и организация здравоохранения. М., 1984. –с.149-158.

· Общественное здоровье и здравоохранение. Под ред. В.А. Миняева, Н.И. Вишнякова. М. «МЕДпресс-информ», 2002. –с. 110-112.

Дата добавления: 2014-12-24