Тема 5. Структурные средние

Цель занятия: освоить методику расчета средних величин.

Методические указания. Задача 1. Дневная выработка двух комбайнов на уборке озимой ржи характеризуется следующими данными (табл. 77).

Таблица 77 - Дневная выработка двух комбайнов

Дневная выработка, га	Дни работы
1-й комбайн
2-й комбайн

Определите среднюю выработку по каждому комбайну.

Решение:

Для решения задачи воспользуемся средней арифметической простой:

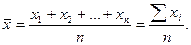(5)

Задача 2. Распределение двух комбайнов по выработке на уборке озимой ржи представлено в таблице 78.

Таблица 78 - Распределение двух комбайнов по выработке

Дневная выработка, га	Количество дней работы за сезон
1-комбайн
2-комбайн

Определите среднюю сезонную выработку по двум комбайнам отдельно, а так же в целом.

Решение:

Для решения задачи воспользуемся средней арифметической взвешенной:

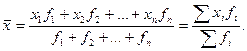(6)

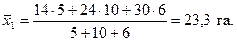
Среднюю сезонную выработку по второму комбайну и в целом определите самостоятельно.

Задача 3. У предпринимателя имеются два автомобиля различных моделей, работающих на бензине одинаковой марки. Расход бензина у первого автомобиля равен 0,05 л/км, у второго – 0,08 л/км. Каков средний расход бензина на 100 км (или на 1 км) пройденного пути?

Решение:

Если для решения задачи мы воспользуемся формулой средней арифметической простой, то мы получим следующее значение:

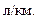
То есть истратив по 1 л бензина два автомобиля вместе проедут

Однако, если рассчитаем по факту расстояние пройденное двумя автомобилями, истратившими по 1 л бензина, то получим:

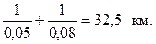
Получается, что формулой средней арифметической простой воспользоваться в этом случае нельзя.

Для решения задачи воспользуемся формулой средней гармонической простой:

(7)

Рассчитаем расстояние, пройденное двумя автомобилями, истратившими по 1 л бензина.

Задача решена верно.

Задача 4. Цена за единицу товара А, продаваемого в первой торговой точке, составила 20 руб., во второй – 30 руб. Какова средняя продажная цена товара, если выручка от продаж товара в торговых точках одинакова?

Решение:

Поскольку весами при расчете средней являются выручки от продажи (товарообороты), а сама выручка представляет собой производственные цены 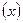на количество проданного товара 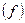, вычисления проводили по средней гармонической взвешенной. Равенство весов позволяет осуществлять расчеты по формуле средней гармонической простой:

Задача 5. Имеются некоторые данные о реализации магазином партии продукции А по дням недели (табл. 79).

Таблица 79 - Данные о реализации магазином партии продукции А

Дни реализации	Исходные данные	Расчетные данные
Цена реализации, руб. за 1 кг	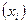Общая выручка за 1 день, руб.	Объем реализованного картофеля, кг
Пятница	5,5
Суббота	5,8
Воскресенье	6,2
Понедельник	5,4
Вторник	5,3
Итого	Х

Определите среднюю цену реализации продукции А за 5 дней.

Решение:

Для решения задачи воспользуемся средней гармонической взвешенной:

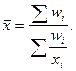(8)

Задача 6. Распределение рабочих предприятия по стажу работы представлено в таблице 80.

Таблица 80 - Распределение рабочих предприятия по стажу работы

Стаж работы в годах	Число рабочих,	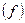Средний интервал,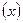
Менее 1		0,5
1 -3		2,0
3-5
5-10		7,5
10-20
20 и более
Итого		X

Требуется дать общую характеристику стажа работы работника предприятия.

Решение:

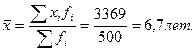
Задача 7. Имеются следующие данные о стаже и производительности труда работников предприятия (табл. 81).

Таблица 81 - Стаж и производительность труда работников предприятия

Номер работника по списку	Производственный стаж, лет	Среднемесячная выработка изделий, шт.

Решение:

По данным таблицы осуществим расчет среднего производственного стажа работников, используя формулу арифметической простой

Применение арифметической средней объясняется тем, что объем варьирующего признака для всей совокупности – общее число проработанных лет работниками (51 год), образуется как сумма стажа каждого работника.

Расчет средней арифметической по данным ряда распределения имеет свои особенности. Проиллюстрируем эти особенности по данным группировки в таблице 82.

Таблица 82 - Расчет среднего производственного стажа работников на основе ряда распределения

Стаж, лет	Число работников, чел.	Середина интервала, лет
1 – 4		2,5	10,0
4 – 7		5,5	27,5
7 – 10		8,5	17,0
Итого		-	54,5

В данном случае следует воспользоваться формулой средней арифметической взвешенной, поскольку интервальные значения признака встречаются не один раз, и эти числа повторений (частоты) не одинаковы.

Конкретными значениями признака, которые должны непосредственно участвовать в расчетах, служат середины (центры) интервалов (но не средние в интервалах значения!), а весами – частоты:

Данный результат отличается от полученного на основе средней арифметической простой. Это объясняется тем, что в расчете на основе ряда распределения мы располагаем не исходными индивидуальными данными, а лишь сведениями о величине середины (центра) интервала.

Задача 8. Т ребуется определить средний темп роста среднегодового валового надоя молока от одной коровы на предприятии за пятилетний период по данным таблицы 83.

Таблица 83 - Динамика среднегодового валового надоя молока от одной коровы на предприятии

Показатели	2007 г.	2008 г.	2009 г.	2010 г.	2011 г.
Среднегодовой валовой надой молока от одной коровы
Цепные темпы роста	-	112,29	99,28	87,66	104,35

Решение:

Для решения задачи воспользуемся формулой средней геометрической:

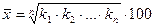(9)

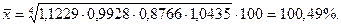
Задача 9. Имеются следующие данные о диаметре труб: первая – 30 см, вторая - 40, третья – 50 см. Определите средний диаметр труб.

Решение:

Для решения задачи воспользуемся формулой средней квадратической простой:

(10)

Задача 10. Известно, что на складе имеются пять труб диаметром 35 см, шесть труб – 40 см и две трубы – 45 см. Определите средний диаметр труб.

Решение:

Для решения задачи воспользуемся формулой средней квадратической взвешенной:

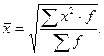(11)

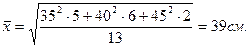
Задача 11. По следующим данным дискретного ряда распределения, расположенного в ранжированном порядке (в порядке возрастания) определите моду и медиану (табл. 84).

Таблица 84 - Стаж работы работников предприятия

Показатель	Номер по порядку рабочего
Стаж работы, лет

Медиана дискретного вариационного ряда, расположенного в ранжированном порядке имеет срединное значение. Когда дискретный ряд включает четное число единиц, то медиана определяется как средняя из двух центральных значений. Таким образом, для данного распределения медиана составит 9 лет, т.е. половина совокупности рабочих имеет стаж работы до 9 лет, половина – более 9 лет.

В дискретном вариационном ряду моду определяют по наибольшей частоте, т.е. 10 лет.

Задача 12. Имеются следующие данные о месячной заработной плате рабочих (табл. 85).

Таблица 85 - Месячная заработная плата рабочих группы малых предприятий одного из регионов

Группы рабочих по размеру заработной платы, руб.	Число рабочих, чел
2000 – 3000
3000 – 4000
4000 – 5000
5000 – 6000
6000 – 7000
Свыше 7000
Итого

Исчислите среднюю заработную плату, моду и медиану заработной платы рабочих малых предприятий.

Решение:

По условию задачи имеется интервальный ряд распределения рабочих, поэтому средняя заработная плата исчисляется по формуле средней арифметической взвешенной (сначала определим середину каждого интервала, т.е. ).

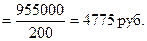
Следовательно, средняя месячная заработная плата рабочих малых предприятий составляет 4775 руб.

Далее исчислим моду по формуле:

(12)

где 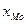– нижняя граница модального интервала,

– величина модального интервала,

– частота модального интервала,

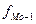– частота интервала предшествующего модальному интервалу,

– частота интервала, следующего за модальным интервалом.

Таким образом, наиболее часто встречающаяся величина средней месячной заработной платы составляет 4533 руб.

Медиану определим по формуле:

(13)

где 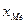– нижняя граница медианного интервала,

– величина медианного интервала,

– сумма частот,

– накопление частот интервала, предшествующего медианному интервалу,

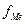– частота медианного интервала.

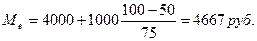
Следовательно, половина рабочих имеет среднемесячную заработную плату меньше 4667 руб., а половина – больше этой суммы.

Задача 13. Имеются следующие данные о заработной плате рабочих (табл. 86).

Таблица 86 - Заработная плата рабочих в цехах предприятия

Цех	Средняя заработная плата, руб.	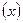Фонд заработной платы, тыс. руб.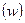
Литейный
Сборочный

Вычислите среднюю заработную плату рабочих по предприятию в целом.

Решение:

Средняя заработная плата рабочих по цехам может быть вычислена делением фонда заработной платы на численность рабочих. Этот подход должен быть сохранен и при расчете общей средней, т.е. в числителе дроби необходимо представить общий по всем цехам фонд заработной платы, а в знаменателе - общую численность рабочих. Однако фонд заработной платы по цехам 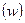есть произведение средних заработков на число рабочих 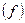. Фонд заработной платы – единственно возможный в данном случае соизмеритель – вес при расчете средней.

Оба эти обстоятельства обуславливают применение средней гармонической, а с учетом того, что заработки по отдельным цехам получают неодинаковые по численности группы рабочих, следует использовать среднюю гармоническую взвешенную. Тогда

Задача 14. По данным таблицы 87 определите моду и медиану.

Таблица 87 - Группировка предприятий по себестоимости единицы продукции

Группы предприятий	Себестоимость одного изделия, руб.	Число предприятий, %
	110 - 115	8,2
	115 - 120	17,2
	120 - 125	23,9
	125 и выше	50,7
Итого		100,0

Решение:

В задании модальным интервалом является, имеющая наибольшую частоту, четвертая группа с интервалом 125 и выше.

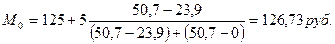
Таким образом, чаще всего встречаются предприятия с уровнем себестоимости на одно изделие 126,73 руб.

Для определения медианного значения признака по формуле находим номер медианной единицы ряда по формуле:

(14)

где 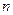- объем совокупности.

В нашем случае:

Необходимо определить, к какой группе относятся предприятия с этими порядковыми номерами. Это можно сделать, рассчитав накопленные частоты. Для установления медианной группы необходимо определять накопленную частоту каждого последующей группы до тех пор, пока она не превысит половины суммы накопленных частот (в нашем случае 50,5) (табл. 88).

Таблица 88 - Определение медианного интервала

Группы предприятий	Себестоимость одного изделия, руб.	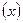Число предприятий, %	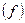Сумма накопленных частот
	110-115	8.2	8,2
	115-120	17,2	25,4
	120-125	23,9	49,3
	125 и выше	50,7
Итого		100,0	X

Медианным является интервал с границами 125 и выше. Определим теперь медиану:

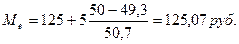
Таким образом, у половины предприятий уровень себестоимости единицы продукции превышает 125,07 руб.

Задача 15. Известно, что пять рабочих имеет стаж от 1 до 4 лет, семь рабочих от 4 до 7 и четверо – от 7 до 10 лет. По данным гистограммы на рисунке 8 определите моду.

Рис. 8. Гистограмма распределения работников по производственному стажу

Решение:

Для того чтобы определить моду необходимо выбрать самый высокий прямоугольник, который является модальным. Затем правую вершину модального прямоугольника соединяем с правым верхним углом предыдущего прямоугольника, а левую вершину модального прямоугольника соединяем с левым верхним углом последующего прямоугольника. Абсцисса точки пересечения этих прямых и будет модой распределения. Таким образом, мода будет 5,2 года.

Задача 16. Определите медиану по кумуляте на рис. 9.

Рис. 9. Кумулята распределения работников по выполнению производственного плана

Решение:

Для определения медианы из точки на шкале накопленных частот, соответствующей 50 %, проводится прямая, параллельная оси абсцисс, до пересечения с кумулятой. Затем из точки пересечения указанной прямой с кумулятой опускается перпендикуляр на ось абсцисс. абсцисса тчоки пересечения является медианой.

Дата добавления: 2014-12-24