Показатели изменения уровней ряда

Понятие и классификация рядов динамики

Ряд динамики – последовательность изменяющихся во времени значений статистического показателя, распложенного в хронологическом порядке.

Составными элементами ряда динамики являются показатели уровней ряда (статистический показатель, характеризующий данное явление за период или на момент времени) и периоды времени (годы, кварталы, сутки) или моменты (даты) времени (периоды времени, которым относятся статистические данные об изучаемом явлении).

Уровни ряда обычно обозначаются через «у», моменты или периоды времени, к которым относятся уровни – через «t».

1. В зависимости от способа выражения уровней ряда ряды динамики делятся на ряды: а) абсолютных; б) относительных; в) средних величин.

2. В зависимости от того, как выражают уровни ряда (на начало месяца или за период), выделяют моментные и интервальные ряды динамики.

3. В зависимости от расстояния между уровнями ряды динамики бывают с равноотстоящими и неравноотстоящими уровнями во времени.

4. В зависимости от наличия основной тенденции изучаемого процесса ряды динамики подразделяются на стационарные и нестационарные.

Анализ скорости и интенсивности явления во времени осуществляется с помощью статистических показателей, которые получаются в результате сравнения уровней между собой. При этом сравниваемый уровень называют отчетным, а уровень, с которым происходит сравнение – базисным.

Различают показатели изменения уровней ряда и средние характеристики рядов динамики. К показателям изменения уровней ряда относятся:

1. Абсолютный прирост:

2. Темп роста:

а) базисный: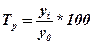

б) цепной:

3. Темп прироста используется для выражения величины абсолютного прироста уровней ряда динамики в относительных величинах:

Он показывает, на какую величину – долю (или процент) уровень данного периода или момента времени больше (или меньше) базисного уровня.

4. Абсолютное значение 1% прироста:

Расчет этого показателя имеет смысл только на цепной основе.

К средним характеристикам ряда относятся:

1. Средний уровень ряда динамики рассчитывается по средней хронологической, исчисленной из значений, изменяющихся во времени.

В интервальных рядах с равноотстоящими интервалами применяется простая средняя арифметическая:

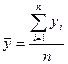
Для интервальных рядов с неравноотстоящими интервалами применяется взвешенная средняя арифметическая:

Для моментных рядов с равноотстоящими интервалами применяется простая средняя хронологическая величина:

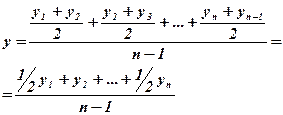
Для моментных рядов с неравноотстоящими интервалами применяется взвешенная средняя хронологическая величина:

2. Средний абсолютный прирост определяется как простая средняя арифметическая величина из цепных абсолютных приростов и показывает, на сколько в среднем изменялся показатель в течение изучаемого периода времени:

3. Среднегодовой темп роста определяется как средняя геометрическая из цепных темпов роста и показывает, сколько процентов в среднем составлял рост показателя.

Если цепные темпы роста опеределялись для рядов с равноотстоящими интервалами, то применяется простая средняя геометрическая величина:

,

где n – количество периодов времени.

Если цепные темпы роста были определены для рядов с неравноотостоящими интервалами, то при расчете среднегодового темпа роста применяется взвешенная средняя геометрическая величина.

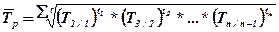
Необходимо помнить, что темпы роста должны быть выражены в виде коэффициентов.

4. Среднегодовой темп прироста определяется также, как и темп прироста и показывает, на сколько процентов в среднем рос показатель в течение изучаемого периода времени.

Дата добавления: 2014-12-24