Закономерность распределения. Изучение формы распределения

Вариация альтернативного признака

Среди множества варьирующих признаков, изучаемых статистикой, существуют признаки, которыми обладают одни единицы совокупности и не обладают другие. Эти признаки называются альтернативными. Альтернативный признак принимает всего два значения – 0 и 1 с весами соответственно p и q. Поэтому среднее значение альтернативного признака равно р. А дисперсия альтернативного признака равна pq. Дисперсия альтернативного признака равна произведению доли признака, обладающего характеристикой на долю признака, не обладающего характеристикой. Предельное значение дисперсии для альтернативного признака равно 0,25 при р=0,5.

Дисперсия альтернативного признака широко применяется в выборочном обследовании.

Закономерностями распределения называются закономерности изменения частот в вариационных рядах.

Основная задача анализа вариационных рядов заключается в выявлении подлинной закономерности распределения путем исключения влияния второстепенных, случайных для данного распределения факторов.

Если увеличить объем совокупности и уменьшить интервал в группах, то графическое изображение приближается к некоторой плавной кривой, которая называется кривой распределения.

Кривая распределения – графическое изображение в виде непрерывной линии изменения частот в вариационном ряду, функционально связанного с изменением вариант.

Теоретическая кривая распределения – кривая, выражающая общую закономерность данного типа распределения в чистом виде, исключающего влияние случайных для него факторов.

Выяснение общего характера распределения предполагает оценку его однородности, а также расчет показателей асимметрии и эксцесса.

При сравнительном изучении асимметрии нескольких распределений с разными единицами измерения вычисляется относительный показатель асимметрии:

Его величина может быть положительной (для правосторонней асимметрии) и отрицательной (для левосторонней асимметрии).

Применение данного показателя дает возможность определить не только величину асимметрии, но и проверить ее наличие в генеральной совокупности. Принято считать, что асимметрия выше 0,5 (независимо от знака) считается значительной. Если асимметрия меньше 0,25, она считается незначительной.

Наличие асимметрии в генеральной совокупности проверяется с помощью определения оценки существенности на основе средней квадратической ошибки:

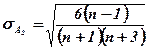
В случае, если 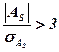, асимметрия считается существенной и распределение признака в генеральной совокупности несимметрично и неслучайно, а закономерно.

Для симметричных распределений может быть рассчитан показатель эксцесса, который показывает, насколько резкий скачок имеет изучаемое явление. Показатель эксцесса определяется на основе центрального момента четвертого порядка по формуле:

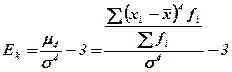
Если показатель эксцесса больше нуля, то распределение островершинное и скачок считается значительным, если коэффициент эксцесса меньше нуля, то распределение считается плосковершинным и скачок считается незначительным. Среднеквадратическая ошибка эксцесса показывает, насколько существенен скачок в явлении и рассчитывается по формуле:

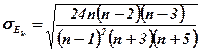
Дата добавления: 2014-12-24