Wariancja zmiennej losowej

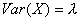
Rozkład Poissona stosujemy wszędzie tam, gdzie liczba obserwowanych doświadczeń niezależnych N w przestrzeni lub czasie jest bardzo duża, a prawdopodobieństwo sukcesu w pojedyńczym doświadczeniu p bardzo małe. Przykłady:
- rozpad promieniotwórczy: liczba jąder n duża, prawdopodobieństwo rozpadu konkretnego jądra bardzo małe;
- zderzenia cząstek elementarnych, duża ilość cząstek, mała szansa na zderzenie;

3. Przedstaw rozkład normalny (Caussa Larlace’a).Podaj ego własności I wyjaśnij wszystkie symbole we wzorze na funkcję gęstości prawdopodobięstwa.

Rozkład zwany rozkładem Gaussa-Laplace'a jest najczęściej spotykanym rozkładem zmiennej losowej ciągłej.Mówimy, że zmienna losowa ciągła X ma rozkład

normalny o wartości oczekiwanej µ i odchyleniu standardowym σ

X ~ N (µ σ)

Rozkład prawdopodobieństwa w przypadku zmiennej losowej ciągłej nosi nazwę rozkładu (funkcji) gęstości. Funkcja gęstości w rozkładzie normalnym o postaci:

określona została dla wszystkich rzeczywistych wartości

zmiennej X.

Funkcja gęstości w rozkładzie normalnym:

- jest symetryczna względem prostej x = µ

- w punkcie x = µ osiąga wartość maksymalną

- ramiona funkcji mają punkty przegięcia dla x = µ - σ

oraz x = µ + σ

- kształt funkcji gęstości zależy od wartości parametrów:

µ i σ. Parametr µ decyduje o przesunięciu krzywej,

natomiast parametr σ decyduje o „smukłości” krzywej.

Funkcja gęstości rozkładu normalnego ma zastosowanie do reguły „trzech sigma”, którą następnie rozwinięto na regułę „sześć sigma” – stosowaną w kontroli jakości, przede wszystkim w USA (np. General Electric, General Motors Company) Reguła „trzech sigma” - jeżeli zmienna losowa ma rozkład normalny to:

- 68,3 % populacji mieści się w przedziale (µ - σ; µ + σ)

- 95,5 % populacji mieści się w przedziale (µ - 2σ; µ + 2σ)

- 99,7 % populacji mieści się w przedziale (µ - 3σ; µ + 3σ)

Prawdopodobieństwo w rozkładzie normalnym wyznacza się dla wartości zmiennej losowej z określonego przedziału

Natomiast:

W celu obliczenia prawdopodobieństwa zmiennej X w

rozkładzie normalnym o dowolnej wartości oczekiwanej µ i odchyleniu standardowym σ dokonuje się standaryzacji. Standaryzacja polega na sprowadzeniu dowolnego rozkładu

normalnego o danych parametrach µ i σ do rozkładu standaryzowanego (modelowego) o wartości oczekiwanej µ = 0 i odchyleniu standardowym σ = 1. Zmienną losową X zastępujemy zmienną standaryzowaną U, która ma rozkład N(0,1)

Zatem :

Własności dystrybuanty standaryzowanego rozkładu normalnego:

4.Na czym polega standartyzacja zmiennej w rozkładzie normalnym.Podaj funkcję gęstości zmiennej standartyzowanej

Aby mówić o rozkładzie normalnym standaryzowanym, należy w pierwszym rzędzie zająć się zagadnieniem standaryzacji zmiennej losowej. Proces ten jest nieskomplikowany, polega on bowiem na odnalezieniu standaryzowanej zmiennej U, co jest niczym innym, jak obliczeniem jej odchylenia standardowego i kolejnym ilorazom, różnicy każdej z osobna realizacji zmiennej X i jej średniej arytmetycznej, co zapisać można w postaci: U = (X - m)/Odchylenie standardowe_X. Standaryzowany rozkład normalny SN jest określany w całości przez dwa parametry, a mianowicie; wartość oczekiwaną E(U) = 0 oraz przez wariancję i odchylenie standardowe równe: D²(U) = D(U) = 1.
W rezultacie procesu standaryzacji zmiennej losowej,b>X_C otrzymujemy transformację rozkładu normalnego z danymi parametrami na standaryzowany rozkład normalny z parametrami określonymi liczbowo, czyli N(0,1), dla którego funkcja gęstości F(u)u przybiera następującą postać:

dla wszystkich możliwych realizacji zmiennej standaryzowanej U.

Szczególnie ważne znaczenie ma w praktyce dystrybuanta zmiennej standaryzowanej U, definiowana podobnie, jak dystrybuanta rozkładu normalnego, czyli:

z tym, jednak iż:



Poziomy dystrybuant można odczytywać z tablic statystycznych posługując się zależnością następującą; dla u większego od 0

5.Jak oblicza się wartość średnia (nadzieję matematyczną) w przypadku zmiennej Losowej skokowej i ciąglej

Wartość oczekiwaną często - potocznie - nazywa się wartością średnią.

Wartość oczekiwana

— Wartością oczekiwaną (wartością przeciętną, wartością średnią, nadzieją matematyczną) zmiennej losowej Xtypu skokowego o rozkładzie pi= P(X = xi), gdzie i ∈ {1,2,...}, nazywamy liczbę

przy założeniu, że suma jest skończona albo szereg nieskończony

Wartość oczekiwana

— Wartością oczekiwaną zmiennej losowej X typu ciągłego o funkcji gęstości prawdopodobieństwa f nazywamy liczbę

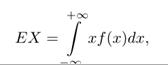
przy założeniu, że całka

Podstawowe własności wartości oczekiwanej

— E(aX + b) = aEX + b, gdzie a,b ∈ R

— jeżeli X i Y są dowolnymi zmiennymi losowymi, dla których istnieją wartości oczekiwane EX oraz EY, to E(X +Y) = EX + EY

— jeżeli istnieje E|X|, to prawdziwa jest nierówność |EX|? E|X|

— wartość oczekiwana jest miarą położenia, parametrem pozycyjnym: wskazuje punkt środkowy rozkładu, tzn. punkt,wokół którego grupują się wartości zmiennej losowej

— interpretacja fizyczna: wartość oczekiwaną można utożsamiać z pojęciem środka ciężkości, jeśli prawdopodobieństwa zinterpretujemy jako masy

Uwaga. Jak wynika z definicji, wartość oczekiwana dla niektórych zmiennych losowych nie istnieje (odpowiedni szereglub odpowiednia całka nie są zbieżne)

6. Jak oblicza się wariację zmiennej Losowej skokowej i ciąglej

Wariancja

— Wariancją zmiennej losowej X nazywamy liczbę

— Jeżeli X jest zmienną losow ą typu skokowego o rozkładzie pi= P(X = xi), i ∈ {1,2,...}, i wartości oczekiwanej EX = m, to

— Jeżeli X jest zmienną losową typu ciągłego o funkcji gęstości prawdopodobieństwa f i wartości oczekiwanej EX =m, to

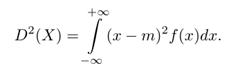
Podstawowe własności wariancji

— D2(X) = E(X2) − (EX)2

— D2(aX + b) = a2D2(X), gdzie a,b ∈ R

— D2(X) більше рівне 0 dla dowolnej zmiennej losowej X

— wariancja jest miarą rozrzutu (rozproszenia) wartości zmiennej losowej wokół wartości oczekiwanej

7.Co to jest dystrybuanta zmiennej Losowej skokowej i ciąglej

Dystrybuanta zmiennej losowej

Niech x oznacza liczbę rzeczywistą, zaś X zmienną losową. Dla każdego x można obliczyć prawdopodobieństwo tego, że zmienna X przyjmie wartość mniejszą lub równą x:

P(X <= x)

Dystrybuantą zmiennej losowej X nazywamy funkcję F określoną na zbiorze liczb rzeczywistych taką, że:

F(x) = P(X <= x)

(2.2.1)

Z określenia dystrybuanty wynikają następujące jej własności:

1) 0 <= F(x) <= 1, dla x Î R

2) lim_{x-> oo} F(x) = 0 oraz lim_{x-> oo} F(x) = 1

3) Dystrybuanta jest funkcją niemalejącą, to znaczy, że dla dowolnych x₁ i x₂ takich, że x₁ < x₂ zachodzi nierówność F(x₁)<=F(x₂).

Uwaga:

W niektórych podręcznikach przy określaniu dystrybuanty wprowadza się zamiast 2.2.1 definicję: F(x) = P (X < x).

Dystrybuanta zmiennej losowej ciągłej X wyraża się wzorem:

(2.4.2)

Funkcja gęstości jest w praktyce ciągła w całym obszarze zmienności X, ewentualnie z wyjątkiem co najwyżej skończonej liczby punktów, oraz ma następujące własności:

1) f(x) >= 0
2) .

Funkcja gęstości pozwala obliczać prawdopodobieństwo, że wartości zmiennej losowej X należą do dowolnego przedziału o końcach a, b:

(2.4.3)

Z powyższego wzoru widać, że prawdopodobieństwo, iż zmienna losowa ciągła przyjmuje wartości z przedziału (a, b) jest równe polu powierzchni pod wykresem funkcji gęstości w przedziale (a, b).

Mamy ponadto bardzo często wykorzystywaną zależność:

P(a < X < b) = F(b) - F(a)

Ponieważ dystrybuanta jednoznacznie określa rozkład zmiennej losowej, zatem rozkład zmiennej losowej ciągłej można opisać albo za pomocą funkcji gęstości prawdopodobieństwa, albo za pomocą dystrybuanty.

Uwaga.

Należy podkreślić, że dla zmiennych losowych ciągłych nie mówi się o prawdopodobieństwie realizacji przez zmienną konkretnej wartości. Ponieważ prawdopodobieństwo, że zmienna losowa ciągła przyjmuje konkretną wartość zawsze równe jest 0: P(X=x₀)= 0

Stąd też:

P(a < X < b) = P(a <=X < b) = P(a < X <=b) = P(a <=X <=b)

8.Co to znaczy że estymator jest zgodny i niobcziążony

Estymator

Załóżmy, że rozkład zmiennej losowej X w populacji generalnej zależy od nieznanego parametru θ.

Estymatorem parametru θ rozkładu zmiennej X nazywamy taką statystykę

będącą funkcją próby losowej pobranej z tej populacji, której rozkład prawdopodobienstwa zależy od szacowanego parametru

Własności estymatorów

+Zgodność

• Nieobciążoność

Zgodność

Estymator parametru θ nazywamy zgodnym, jeżeli jest

stochastycznie (w sensie prawdopodobie?stwa) zbieżny do

szacowanego parametru

Interpretacja:

wraz ze wzrostem liczności próby wzrasta dokładność oszacowania parametru θ.

Nieobciążoność

Estymator jest nieobciążony jeżeli:

Interpretacja

Własność nieobciążoności oznacza, że przy wielokrotnym losowaniu próby średnia z wartości przyjmowanych przez estymator nieobciążony równa się wartości szacowanego parametru. Własność ta gwarantuje otrzymanie za jego pomocą ocen wolnych od błędu systematycznego.

Zgodność i nieobciążoność

Współzależności pomiędzy własnościami zgodności i nieobciążoności:

• jeżeli estymator θn parametru jest zgodny, to równocześnie jest asymtotycznie nieobciążony; twierdzenie odwrotne nie jest prawdziwe

• jżeli estymator θn parametru θ jest nieobciążony (lub asymptotycznie nieobciążony) oraz jeżeli jego wariancja w miarę wzrostu liczebno?ci próby zmierza do zera, to θn jest estymatorem zgodnym

9. Jak bada się efektywnośćestymatora określonego parametru populacji generalnej. Jak interprytuje się twz. Błąd estymatora

Aby ułatwić opis populacji wyróżnia się jej cechy (np. wzrost osobników, ich masę). Cechę można traktować jako zmienną losową, a wartości cechy poszczególnych elementów populacji – jako realizacje zmiennej losowej. Stąd też do charakterystyki populacji używamy wszystkich tych pojęć, które charakteryzują zmienną losową; możemy w szczególności określić rozkład populacji i parametry tego rozkładu.

Wartości parametrów charakteryzujących populację na ogół nie są znane, można je jednak w przybliżeniu oszacować na podstawie próby. Tak otrzymaną wartość nazywamy estymatorem danego parametru. Jeżeli x ₁, x ₂,..., x_n oznaczają wartości poszczególnych elementów próby, to estymatorem wartości średniej (oczekiwanej) cechy X w populacji jest średnia arytmetyczna elementów próby:

[1]

natomiast estymatorem wariancji jest wariancja z próby:

[2]

W konkretnej próbie otrzymamy konkretną wartość estymatora (ocenę parametru). Jednak dla różnych prób pobranych z tej samej populacji uzyska się na ogół inne oceny, ponieważ próby są kompletowane losowo i jest rzeczą przypadku, które elementy populacji zostaną pobrane. Estymator danego parametru można zatem traktować jako zmienną losową, a ta ma swoją wartość oczekiwaną i wariancję. Standardowe odchylenie estymatora nazywa się jego błędem standardowym.

Wielkość będącą funkcją elementów próby (tzn. określoną na podstawie elementów próby), nazywamy statystyką, a więc każdy estymator jest statystyką.

Jeden parametr może mieć wiele estymatorów. Estymatorem wartości oczekiwanej, na przykład, jest nie tylko średnia arytmetyczna, ale również modalna (wartość najczęstsza w próbie) czy też mediana.

Medianą nazywa się wartość środkowego elementu próby uporządkowanej według wartości rozpatrywanej cechy; gdy liczba elementów próby jest parzysta, za medianę się przyjmuje średnią arytmetyczną wartości elementów środkowych; np. w 6-elementowej próbie o wartościach: 3, 5, 5, 8, 9, 9 mediana jest równa: (5+8)/2 = 6,5.

Nie ma jednego kryterium, które pozwoliłoby określić, który estymator danego parametru jest najlepszy.; Wyróżnia się kilka kryteriów porównawczych, spośród których omówimy tutaj 3 najważniejsze.

Nieobciążoność. Estymator t danego parametru q jest nieobciążony, jeżeli jego wartość oczekiwana jest równa wartości parametru w populacji:

E (t) = q.

Gdy estymator jest nieobciążony, to po wyborze bardzo (nieskończenie) wielu prób losowych z populacji i ocenie parametru w każdej z nich okaże się, że średnia tych ocen jest równa wartości parametru w populacji. Średnia arytmetyczna (wzór [1]) jest estymatorem nieobciążonym wartości średniej populacji, m, natomiast wariancja dana wzorem [2] własności takiej nie ma; estymatorem nieobciążonym wariancji s ² jest:

[3]

Zgodność. Estymator nazywamy zgodnym, jeżeli wraz ze wzrostem liczebności próby wartość estymatora zbliża się dowolnie blisko do wartości parametru w populacji. Estymatorami zgodnymi są zarówno średnia arytmetyczna, jak i wariancje dane wzorami [2] i [3].

Efektywność. Miarą efektywności estymatora jest jego błąd standardowy. Mały błąd standardowy oznacza, że oceny parametru uzyskane z różnych prób (tej samej wielkości) będą bardzo skupione wokół wartości parametru w populacji. Estymator o najmniejszym błędzie standardowym nazywa się estymatorem najefektywniejszym. Najefektywniejszym estymatorem wartości średniej w populacji jest średnia arytmetyczna.

10.Jakie znasz estymatory średniej wartości zmiennej (nadziei matematycznej) w populacji generalnej. Ktory z nich jesz estymatorem najliepszym i dla czego.

estymatorem wariancji wartości średniej będzie:

A estymatorem dyspersji wartości średniej:

Powyższe wyrażenie nazywamy odchyleniem standardowym wartości średniej Odchylenie standardowe wartości średniej jako funkcja zmiennej losowej jest zmienną losową. Oznacza to, że podobnie jak odchylenie standardowe pojedynczego pomiaru jest ono tylko oszacowaniem dyspersji wartości średniej a nie dokładną wartością tej dyspersji. Odchylenie standardowe średniej przyjmowane jest jako niepewność pomiaru.

11.Jak ustalić właćciwą liczebność proby statystycznej w przypadku estymacji wartości średnej określonej zmiennej losowej

Model dla małej próby

Jako małą przyjmuje się traktować próbę o liczebności . Estymatorem dla oszacowania wartości średniej w populacji generalnej jest średnia z próby . Przyjmuje się założenie, że rozkład badanej zmiennej w populacji generalnej ma charakter rozkładu normalnego. Z populacji tej losowana jest próba i na podstawie uzyskanych z niej danych wyznaczana jest wartość średnia i odchylenie standardowe . Z góry zakładany jest poziom ufności 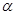. Przedział ufności dla wartości średniej w populacji generalnej szacowany jest według wzoru:

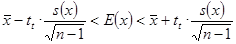
1

Występująca w powyższym wzorze wielkość jest wartością statystyki odczytywaną z tablic rozkładu t Studenta dla oraz . Uzyskany przedział z prawdopodobieństwem równym poziomowi ufności pokrywa nieznaną wartość średnią w populacji generalnej. Warto zwrócić uwagę, iż otrzymany przedział jest symetryczny względem średniej z próby.

Należy zaznaczyć, iż błędna byłaby interpretacja, że szacowana średnia znajduje się w uzyskanym przedziale z prawdopodobieństwem równym 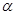, ponieważ to przedział jest zmienny, a nie szacowana wartość średnia (ona jest wielkością stałą). Uwaga ta dotyczy estymacji wszelkich parametrów szacowanych metodą przedziałową.

Przykład 1.

W badaniach rozwoju czytelnictwa wśród młodzieży szkolnej dla losowej próby 15 uczniów klas I – III pewnej szkoły zebrano informacje dotyczące liczby przeczytanych książek w roku szkolnym. Otrzymano następujące informacje: 2; 6; 12; 10; 5; 4; 20; 22; 10; 15; 9; 8; 21; 14.; 7; Zakładając, że rozkład przeczytanej liczby książek w całej populacji uczniów jest zbliżony do normalnego - przy poziomie ufności 0,98 - oszacować metodą przedziałową średnią liczbę przeczytanych książek dla tej populacji.

Rozwiązanie

Wylosowana próba jest mała, a więc dla oszacowania przedziału ufności wykorzystamy formułę 1. W pierwszej kolejności wymaga ona wyznaczenia średniej i odchylenia standardowego liczby przeczytanych książek w próbie. Korzystając z odpowiednich wzorów otrzymujemy:

książek

książki.

Dla przyjętego poziomu ufności odczytujemy z tablic rozkładu t Studenta (tablica 2. w Aneksie) wartość statystyki teoretycznej dla oraz 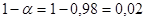. Wynosi ona 2,624. Uzyskane wielkości podstawiamy do podanej formuły:

książek

Przedział ufności o końcach 6,7 i 15,3 książek z prawdopodobieństwem 0,98 zawiera nieznaną średnią liczbę przeczytanych książek przez wszystkich uczniów klas I – III tej szkoły.

Zauważmy, że przedział ten jest symetryczny względem średniej z próby równej 11 książek; połowa jego rozpiętości, tj. jest określana mianem maksymalnego błędu szacunku bądź tolerancją lub precyzją szacowania (oznaczana jest zwykle jako d).

12.Na czym polega estymacja punktowa wskażnika strukury (frakcji). Wyjaśnij wszystkie symbole.

Estymacja punktowa polega na tym, że jako ocenę nieznanego parametru Q populacji generalnej przyjmujemy uzyskaną z wylosowanej próby wartość estymatora . Szacowanie polega w tym przypadku na podaniu jednej konkretnej wartości liczbowej parametru estymowanego. Taki sposób postępowania oznacza, że jeśli z populacji będziemy pobierali kolejne próby, wyznaczali dla każdej z nich wartość estymatora, to można się spodziewać zróżnicowanych wartości liczbowych, a to z kolei może oznaczać, iż dla tej samej populacji istnieje kilka wartości tego samego parametru estymowanego (np. kilka wartości średnich tej samej zmiennej), co jest przecież niemożliwe. Prawdopodobieństwo zajścia zdarzenia, że uzyskana z dowolnej próby wartość estymatora jest identyczna jak faktyczna wartość szacowanego parametru jest praktycznie równe zero, co można zapisać następującą relacją:

13. Przedstaw zasady estymacji przedziałowej wartości średniej (nadziei matymatycunej)

14..Przedstaw zasady estymacji przedziałowej wskażnika struktury(frakcji)

Estymacja przedziałowa dla wskaźnika struktury Załóżmy, że badana cecha X przyjmuje tylko dwie wartości (warianty). Taką cechę okresla się często mianem cechy dychotomicznej. Typowym przykładem jest płeć. Przypuśmy, że interesuje nas jeden z dwóch wariantów cechy X. Niech poznacza udział elementów populacji posiadających wybrany ariant cechy, np. udział kobiet w pewnej zbiorowości osób.Parametr p określa się mianem frakcji elementów wyróżnionych (w skrócie – frakcji lub wskaźnika struktury).

a) MODEL I

Rozważmy próbkę o małej liczebności n. Niech Snoznacza liczbę elementów w próbie posiadających cechę X. Zgotowych tablic odczytujemy przy 95%- towym poziomie

ufności wartości f1(Sn,n,α), f2(Sn,n,α), takie,że

Przedział ufności dla wskaźnika struktury (frakcji) jest postaci:

b) MODEL II - próba duża Zagadnienie estymacji przedziałowej parametru p można

sprowadzić do zagadnienia estymacji średniej w populacji. Korzysta się tu z twierdzeń granicznych. Warunkiem jest więc dysponowanie dostatecznie dużą próbą n bilsh’rivne100 (w praktyce

n > 50).

Дата добавления: 2014-12-24