Поняття вектора

Мішаний добуток векторів.

Векторний добуток векторів.

Скалярний добуток векторів.

Лінійні операції над векторами.

Поняття вектора.

План

Тема 3. Вектори

Означення. Вектором називається напрямлений відрізок. Позначати вектори будемо 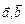,.... Якщо, скажімо, точка А — початок вектора, а точка В — його кінець, то маємо .

Вектор, в якого початок і кінець збігаються, називається нульовим вектором.

Вектор вважається заданим, коли відома його довжина 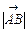, 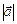і напрям щодо деякої осі.

Два вектори 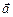і 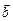називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих.

Вектори 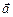і 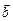вважаються рівними, коли вони: 1) колінеарні; 2) однаково напрямлені; 3) їхні довжини рівні.

Нехай у просторі задано деяку вісь l і вектор . Проведемо через точки А і В площини, перпендикулярно до осі l (рис. 2.7). Позначимо точки перетину цих площин з віссю l відповідно 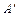і .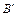

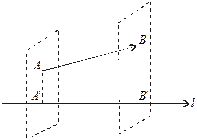Рис. 3.1

Означення. Проекцією вектора на вісь l називається довжина напрямленого відрізка 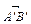на осі l. Слід зазначити, що 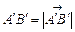, якщо напрям збігається з напрямом l і , якщо напрям протилежний напряму l.

Позначається проекція вектора на вісь l — пр_l . З рис. 2.7 випливає формула знаходження проекції вектора на вісь:

пр_l = ,

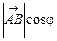де — кут між вектором і віссю.

Якщо розглянути прямокутну декартову систему координат і точки початку А (х ₁, у ₁, z ₁) і кінця В (х ₂, у ₂, z ₂) вектора 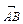, то проекції вектора 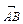на кожну з осей мають вигляд:

Ох: а_х = х ₂ – х ₁, Оу: а_у = у ₂ – у ₁, Оz: а _z = z ₂ – z ₁.

Нехай вектори такі, що за напрямом збігаються відпо-
відно з осями Ох, Оу, Оz і . Такі вектори надалі називатимемо одиничними векторами осей системи координат. Тоді

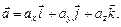(3.3)

Довжина вектора подається формулою:

(3.1)

Якщо позначити a, b, g — кути між вектором 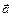і відповідними осями системи координат, то їх косинуси можна знайти за формулами:

. (3.2)

У подальшому називатимемо їх напрямними косинусами вектора 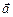. Піднісши кожну з формул (2.5) до квадрата і скориставшись (2.4), дістанемо:

cos²a + cos²b + cos²g = 1.

2. Лінійні операції над векторами

Дії з векторами виконуються за правилами:

1. Додавання: (правило трикутника, паралелограмма)

= (а_х + b_х, а_у + b_у, а_z + b_z).

2. Множення вектора на число a Î R:

.

Для лінійних операцій з векторами виконуються властивості:

1. .

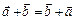2. .

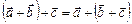3. .

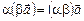4. .

5. .

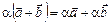Теорема. Проекція суми двох векторів на вісь дорівнює сумі їхніх проекцій на цю вісь:

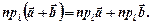
Теорема. При множенні вектора на число його проекція на цю вісь також множиться на це число:

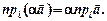
Дата добавления: 2014-12-24