
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Мішаний добуток векторів
|
|
|
|
Означення. Мішаним добутком векторів  називається число, яке дорівнює
називається число, яке дорівнює
 .
.
З означення випливає:
1) Мішаний добуток векторів  дорівнює скалярному добутку вектора
дорівнює скалярному добутку вектора 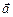 на векторний добуток векторів
на векторний добуток векторів 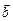 і
і 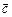 , тобто
, тобто 
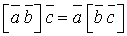 =
=  .
.
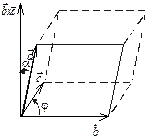 Рис. 3.3
Рис. 3.3
|
Розглянемо геометричний зміст змішаного добутку. Для цього побудуємо на векторах 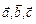 , вважаючи, що вони не лежать в одній площині, тобто не компланарні, паралелепіпед (рис. 2.9).
, вважаючи, що вони не лежать в одній площині, тобто не компланарні, паралелепіпед (рис. 2.9).
Знайдемо об’єм паралелепіпеда, побудованого на векторах  (рис. 2.9). Площа основи його дорівнює модулю векторного добутку векторів
(рис. 2.9). Площа основи його дорівнює модулю векторного добутку векторів 
 . Висота дорівнює
. Висота дорівнює 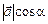 . Отже, остаточно маємо:
. Отже, остаточно маємо:
 . (3.6)
. (3.6)
З останнього випливає, що модуль мішаного добутку чисельно дорівнює об’єму паралелепіпеда, побудованого на векторах  . З рівності (2.9) маємо умову компланарності трьох векторів
. З рівності (2.9) маємо умову компланарності трьох векторів 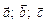 .
.
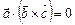 .
.
Властивості мішаного добутку:
1.  .
.
2. 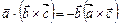 .
.
ПРИКЛАДИ:
1. Дано: 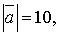
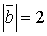 і
і  . Обчислити
. Обчислити  .
.

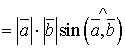 .
. 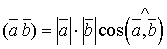 , звідки
, звідки  =
=  . Оскільки
. Оскільки  >0, то
>0, то  .
.
 =
=  =
=  .
.
Отже, 
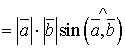 =
= 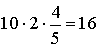 .
.
2. Трикутник задано вершинами А (1; ‑1; 2), В (5; ‑6; 2), С (1; 3; ‑1). Обчислити довжину висоти, опущеної з вершини В на сторону АС.
Розв’язання:
 та
та 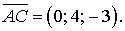
 :
:
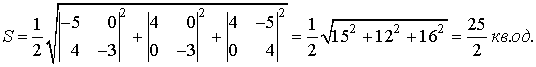
 , тобто
, тобто 
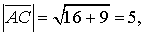 і
і 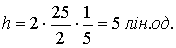
3. На точку А (4; 2; ‑3) діють дві сили 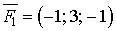 та
та 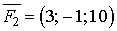 . Знайти момент рівнодіючої цих сил, його величину та напрямні косинуси відносно точки В (2; 4; 0).
. Знайти момент рівнодіючої цих сил, його величину та напрямні косинуси відносно точки В (2; 4; 0).
Розв’язання:
Знайдемо рівнодіючу заданих сил  та вектор
та вектор  момент сили знаходиться за формулою:
момент сили знаходиться за формулою:

Напрямні косинуси вектора моменту сили відповідно дорівнюють

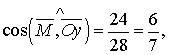

4. Три вершини тетраедра знаходяться в точках А (2; 1; -1), В (3; 0; 1), С (2; -1; 3). Знайти координати четвертої вершини D, яка належить вісі Оу, якщо об’єм тетраедра дорівнює 3 куб. од.
Розв’язання:
Оскільки точка D належить вісі Оу, то її координати 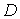 (0; у; 0). Об’єм тетраедра ABCD можна розглядати як
(0; у; 0). Об’єм тетраедра ABCD можна розглядати як  об’єму паралелепіпеда, побудованого на векторах
об’єму паралелепіпеда, побудованого на векторах  як на ребрах:
як на ребрах:
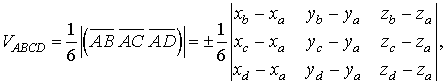
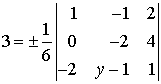 .
.
Розв’язуючи це рівняння, дістанемо, що  отже
отже 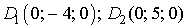 .
.
5. Довести, що чотири точки  лежать в одній площині.
лежать в одній площині.
Розв’язання:
Для того, щоб довести, що чотири точки лежать в одній площині, достатньо довести, що три вектора компланарні. За спільний початок векторів виберемо точку А, тоді:

Вектори 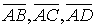 будуть компланарними тоді, коли їх мішаний добуток дорівнює нулеві.
будуть компланарними тоді, коли їх мішаний добуток дорівнює нулеві.

 = ‑2+12‑8‑2=0.
= ‑2+12‑8‑2=0.
Отже, одержали, що вектори  компланарні, тому точки A, B, C, D належать одній площині.
компланарні, тому точки A, B, C, D належать одній площині.
6. Задана піраміда з вершинами в точках А (1; 2; 3), В (‑2; 4; 1), С (7; 6; 3), D (4; ‑3; ‑1). Знайти:
а) довжину ребер  ;
;
б) площу грані АВС;
в) кут між ребрами 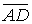 і
і 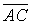 ;
;
г) об’єм піраміди;
д) довжину висоти, опущеної на грань АВС.
Розв’язання:
а) Знайдемо вектори  .
.
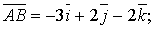
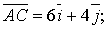

Знайдемо модулі цих векторів:



б) Площа грані АВС буде дорівнювати:
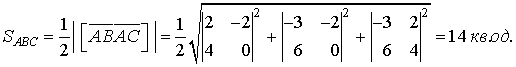
в) Кут між ребрами 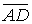 і
і 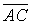 знайдемо за формулою:
знайдемо за формулою:
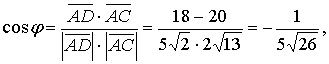

г) Об’єм піраміди обчислимо за формулою:

д) Довжину висоти h, опущеної на грань АВС, можна знайти, користуючись формулою:
 звідки
звідки 
Таким чином 
|
|
|
|
|
Дата добавления: 2014-12-24; Просмотров: 3896; Нарушение авторских прав?; Мы поможем в написании вашей работы!