
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Векторний добуток векторів
|
|
|
|
Скалярний добуток векторів
Означення. Скалярним добутком двох векторів 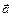 і
і 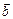 називається число (скаляр), яке дорівнює сумі добутків їх відповідних координат.
називається число (скаляр), яке дорівнює сумі добутків їх відповідних координат.
Отже, 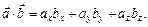
Теорема. Скалярний добуток двох ненульових векторів 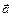 і
і 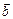 дорівнює добутку модулів цих векторів на косинус кута між ними. Якщо хоча б один із векторів дорівнює нулю, то кут між векторами не визначений і за означенням скалярний добуток дорівнює нулю.
дорівнює добутку модулів цих векторів на косинус кута між ними. Якщо хоча б один із векторів дорівнює нулю, то кут між векторами не визначений і за означенням скалярний добуток дорівнює нулю.
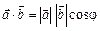 ,
,
де j — кут між векторами. Використовуючи формулу проекції вектора, можна також записати:
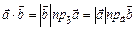 .
.
Наслідок: Кут між двома векторами 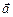 і
і 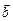 можна знайти за формулою:
можна знайти за формулою:
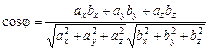 .
.
Властивості скалярного добутку:
1. 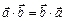 . 4.
. 4. 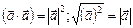 .
.
2. 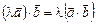 . 5.
. 5. 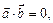 якщо
якщо 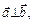 і навпаки,
і навпаки,
3. 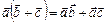 .
. 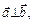 якщо
якщо 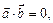
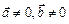 .
.
Означення. Векторним добутком вектора 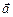 на вектор
на вектор 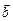 називається вектор
називається вектор
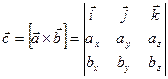
З означення випливає:
1) довжина вектора 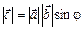 , де j — кут між двома векторами;
, де j — кут між двома векторами;
2) вектор 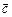 перпендикулярний до кожного з векторів
перпендикулярний до кожного з векторів 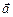 і
і 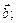
 Рис. 3.2
Рис. 3.2
|
3) вектор 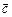 спрямований так, що коли дивитися з його кінця на площину, в якій лежать вектори
спрямований так, що коли дивитися з його кінця на площину, в якій лежать вектори 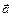 і
і 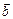 , то поворот вектора
, то поворот вектора 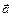 до вектора
до вектора 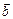 відбувається на найменший кут проти годинникової стрілки.
відбувається на найменший кут проти годинникової стрілки.
Геометричний зміст: Модуль векторного добутку двох неколінеарних векторів дорівнює площі паралелограма, побудованого на векторах як на сторонах.
Властивості векторного добутку:
1. 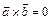 , якщо
, якщо 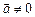 і
і  — колінеарні вектори.
— колінеарні вектори.
2. 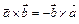 .
.
3. 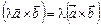 .
.
4. 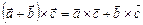 .
.
Якщо вектори-множники взаємно перпендикулярні, то модуль векторного добутку дорівнює добутку модулів співмножників:
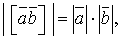 якщо
якщо 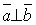 .
.
Якщо вектори-множники колінеарні, то 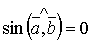 і векторний добуток їх дорівнює нуль-вектору, тобто
і векторний добуток їх дорівнює нуль-вектору, тобто
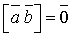 .
.
Знайдемо векторні добутки одиничних векторів 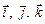 . З колінеарності векторів випливає:
. З колінеарності векторів випливає: 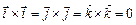 . З того, що одиничні вектори збігаються з напрямом осей прямокутної системи координат, маємо:
. З того, що одиничні вектори збігаються з напрямом осей прямокутної системи координат, маємо:
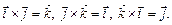
Механічний зміст: Якщо 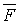 є вектор сили, прикладеної до деякої точки В, а вектор
є вектор сили, прикладеної до деякої точки В, а вектор 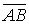 , спрямований з точки А в точку В, то векторний добуток
, спрямований з точки А в точку В, то векторний добуток 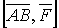 буде моментом
буде моментом 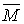 сили
сили 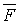 відносно точки А.
відносно точки А.
|
|
|
|
|
Дата добавления: 2014-12-24; Просмотров: 2842; Нарушение авторских прав?; Мы поможем в написании вашей работы!