Моделирование системы с регулятором положения

Для решения задачи по перемещению механизма в заданное положение (позицию) применяют системы с регулятором положения. Часто эти системы называют позиционными. К таким системам можно отнести электропривод нажимного устройства, летучих ножниц, манипуляторов и т.д. Структурная схема позиционной системы приведена на рис. 18а. Модель системы в программе АС 3.1 приведена на рисунке 18б.(файл POS1.sa). Внутренние контуры регулирования: контур тока якоря и контур частоты вращения рассмотрены в предыдущих разделах. Остановимся подробнее на внешнем контуре положения и звеньях, входящих в этот контур. Заданное и текущее значения регулируемой координаты обозначены соответственно S_З и S.

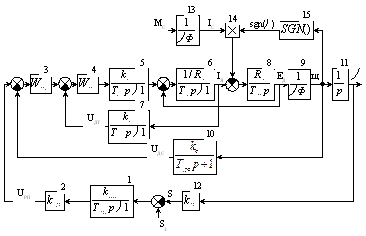
а)

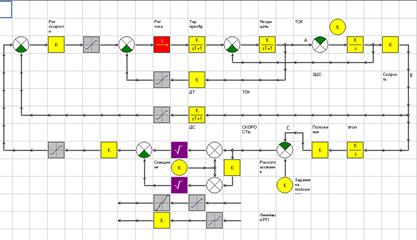
б)

Рис. 18.

Звено № 11 связывает частоту вращения двигателя и угол поворота вала. По характеру – это интегратор без ограничения выходной переменной.

Звено № 12 является коэффициентом связи между углом поворота вала двигателя и регулируемой координатой позиционной системы S. Рассмотрим несколько частных случаев расчета этого коэффициента.

а) Регулируемой координатой является угол поворота вала двигателя. В этом случае k_П = 1.Под параметром S следует понимать заданное и текущее значение угла поворота вала двигателя.

б) Регулируется угол поворота механизма, связанного с двигателем редуктором с передаточным числом i. Обычно i определяется, как отношение скоростей или углов поворота входного и выходного валов редуктора (при этом коэффициент передачи редуктора ). В этом случае .

в) Отрабатывается линейное перемещение механизма, например перемещение нажимного винта прокатного стана, вращаемого электродвигателем через редуктор с передаточным числом i. Введя обозначение шага винта h, для определения k_П получим выражение: .

В общем случае коэффициент k_П следует рассчитывать, исходя из кинематической схемы механизма и его параметров.

Звено № 1 представляет собой передаточную функцию измерительно-преобразующего устройства (ИПУ). Этот элемент системы преобразует рассогласование между заданным и текущим значениями регулируемой угловой или линейной координаты в напряжение соответствующей величины и полярности. В зависимости от того, какой является система регулирования положения: цифровой (дискретной) или аналоговой аппаратная реализация ИПУ может быть различной.

В дискретных системах для контроля перемещения или положения используют импульсные или позиционно-кодовые датчики. Для реализации ИПУ применяют счетчики, сумматоры, цифроаналоговые преобразователи.

В аналоговых системах используют сельсины, поворотные трансформаторы, потенциометры, связанные с валом двигателя или механизма. При необходимости эта связь осуществляется через редуктор. Преобразование переменного напряжения сельсина в постоянное соответствующей величины и полярности производится с помощью фазочувствительного выпрямителя.

В модели ИПУ аппроксимировано апериодическим звеном. В ряде случаев инерционностью устройства можно пренебречь и аппроксимировать его безынерционным усилителем с ограничением выхода. Коэффициент звена можно рассчитать по формуле:

,

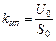где U₀ – принятый уровень максимального напряжения ИПУ, S₀ – соответствующее этому уровню угловое или линейное рассогласование между заданным и текущим значением.

В качестве S₀ принимают так называемый минимальный угол (путь) торможения с номинальной скорости до останова, (предполагается, что торможение производится с максимальным отрицательным ускорением). Для расчета используются известные формулы из теории электропривода и теоретической механики.

,

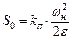где ω_н – номинальная частота вращения двигателя, ε – угловое ускорение при торможении, J – приведенный к валу двигателя момент инерции, М_ДТ и М_с – максимальный момент двигателя при торможении и момент статического сопротивления.

Звено № 2 моделирует регулятор положения. В позиционных системах применяют как линейные, так и нелинейные (параболические) регуляторы положения.

В настоящее время для регулирования положения применяются не аналоговые, а цифровые системы регулирования. Регулятором является, как правило, программируемый логический контроллер (ПЛК), преобразующий рассогласование ΔS = S_з – S в задание на скорость электропривода. Если регулирование скорости осуществляется аналоговым регулятором, то контроллер преобразует ΔS в соответствующий уровень напряжения, подаваемого в качестве задания на вход регулятора скорости. При использовании контроллера в качестве регулятора скорости результаты расчета алгоблока регулирования положения являются входными данными алгоблока регулирования скорости электропривода.

При таком подходе в модели звенья 1 и 2 объединяются в один элемент – регулятор положения (контроллер), выполняющий одновременно функции измерительно-преобразующего устройства и собственно регулятора(линейного или параболического).

Из литературы известно [6], что задание на скорость(выход регулятора положения) и рассогласование по положению связана соотношением:

В этом случае обеспечивается торможение с максимальной интенсивностью и минимальный путь торможения S₀ при торможении с номинальной скорости. Значение коэффициента К зависит от размерности ΔS и величины максимального задания на скорость.

Статическая характеристика регулятора положения приведена на рисунке:

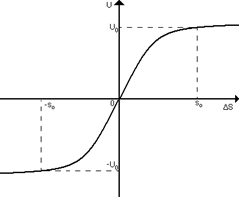
При ΔS ≤ S₀ выход и вход связаны зависимостью , а при ΔS > S₀ выход регулятора постоянен и равен максимальному заданию на скорость U ₀, например 10В

Для улучшения работы позиционной системы начальные участки параболы линеаризуются и вводится порог чувствительности регулятора. В этом случае ветви параболы смещаются на величину S_c относительно начала координат и характеристика окончательно выглядит так:

Звенья № 14 и № 15 введены в модель для того, чтобы учесть изменение знака нагрузки в зависимости от направления перемещения.

Контур тока якоря и частоты вращения (скорости) были рассмотрены ранее (звенья 3–10).

Ниже приведены данные модели, взятые из описания механизма и полученные расчетным путем (формулы и расчеты не приведены).

i=50; k_П =0,02; M_H=83 H*м; M_C=20 H*м; k_C=0,095; Т_ДС=0,03с; М_ДТ=208; k_РС=6,6; ε=160; S₀=0,7.

; .

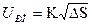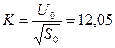В позиционных системах применяют также и линейные регуляторы положения. Коэффициент регулятора можно рассчитать по формуле:

Ниже приведены результаты расчета контура положения, в которых использованы данные двухконтурной системы регулирования скорости.

Было задано отработать поворот на 360° без нагрузки. Результаты моделирования представлены на рисунке. График 1 соответствует изменению тока, график 2 отражает изменение скорости при отработке перемещения, изображенного на графике 3. Графики изображены в относительных единицах.

Дата добавления: 2014-12-24