До розд. 3.2) Переваги і недоліки рекурсивних визначень функцій і процедур

Додаткові відомості

Питання для роздумів

Фрактальна множина (фрактал), фрактальний трикутник.

1. Як Ви думаєте, чому принципово не можна вирішити задачу про визначення довжини берегової лінії острівної держави? (Навіть при наявності дуже детальної карти і невисоких вимог до точності результату.)
2. Як Ви думаєте, яким буде результат роботи програми коду 3.14, якщо в процедурі НамалюватиТрикутник замінити малювання трикутника малюванням чого-небудь іншого, наприклад кольорового прямокутника?

Ідеї рекурсії використовуються в наукових дослідженнях уже багато століть. Рекурсивні визначення — це досить потужний інструмент наукового аналізу.

Використання рекурсивних визначень у програмуванні теж буває дуже корисним і приваблює своєю красою і лаконічністю.

До переваг рекурсивних визначень функцій і процедур можна віднести такі:

• легко майже дослівно програмувати обчислення за рекурентними формулами (Рекурентна формула (від лат. recurrentis — що повертається) — це формула, за якою можна знаходити значення деякого члена послідовності за значеннями декількох попередніх йому членів);
• легко доводиться коректність програми — її еквівалентність тим формулам, за якими вирішується задача;
• за допомогою кінцевого виразу можна визначити нескінченну множину об'єктів;
• програмні коди відрізняються простотою, наочністю і компактністю запису.

Основними недоліками рекурсивних визначень є:

• неефективна витрата оперативної пам'яті. Для кожного рекурсивного виклику однієї і тієї ж функції (процедури) виділяються нові комірки пам'яті. Щоразу створюється нова копія цієї функції (процедури) і всі локальні змінні цієї копії вимагають нових місць у пам'яті;
• швидкість роботи програм з рекурсивними визначеннями, як правило, у багато разів менша від швидкості роботи програм, що вирішують ті ж задачі без використання рекурсивних визначень.

Можна зробити такий висновок: не слід занадто захоплюватися рекурсивними визначеннями. Є мови програмування, у яких буквально все «пронизано» рекурсією. До них відносяться Лісп і Пролог. У цих мовах головне не обчислення, а обробка текстів символьної, а не числової інформації. Говорять, що на цих мовах добре вирішуються задачі штучного інтелекту. В алгоритмах для таких задач рекурсія буває іноді єдиним ефективним інструментом.

Наведемо приклад, що добре ілюструє переваги і недоліки рекурсивних визначень.

Приклад 3.6. Згадаємо визначення числової послідовності (ряду) Фібоначчі: «Кожен наступний член цього ряду (за винятком перших двох) дорівнює сумі двох попередніх членів. А перші два члени ряду — одиниці».

Визначимо функцію Фібоначчі(N), аргументом якої є номер числа в ряді Фібоначчі, а значенням — саме це число:
Фібоначчі(І) = 1; Фібоначчі(2) = 1;
Фібоначчі(N) = Фібоначчі(N - 2) + Фібоначчі(N - 1), якщо N > 2.

Ви бачите, що в цьому визначенні використовується рекурентна формула. З її допомогою легко дати визначення рекурсивної функції Фібоначчі(N):

Код 3.15

Аналогічно можна визначити і рекурсивну процедуру, вихідним параметром якої є N-e число Фібоначчі:

Код 3.16

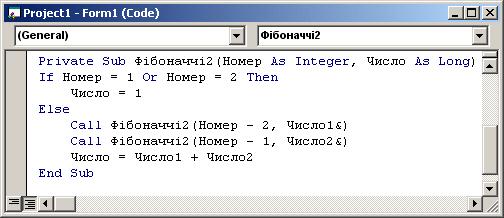
Добірність і лаконічність наведених визначень не викликає сумнівів. Однак у роботі ці процедури показують себе не з кращої сторони — вони працюють дуже повільно.

У багато разів швидше працюють програми, що обчислюють значення N-го числа Фібоначчі без застосування рекурсії.

Інший варіант — це розрахунок за формулою:

Фібоначчі(N) = (((1+ Sqr(5)) / 2)^N -- ((1- Sqr(5)) / 2)^N) / Sqr(5).

(Формула була отримана теоретично.)

Код3.17

Дуже явно недоліки рекурсивних визначень чисел Фібоначчі виявляють себе в тому випадку, коли потрібно знаходити не одне N-і число, а весь ряд від 1-гo до N-го числа. І простій процедурі — рішенню немає рівних. Ряд, що складається з 30 членів, проста процедура обчислює в 1000 разів швидше, ніж програма з рекурсивним визначенням (коди 3.15 чи 3.16). Якщо ж ряд містить більш 30 членів, рекурсивна процедура на Вашому комп'ютері не візьме його зовсім, а проста процедура справиться навіть з таким, що містить 44 члена, за 0.05 сек! (Фібоначчі(44) = 701408733).

Hові поняття:

Дата добавления: 2014-12-23