Розв’язання. Характеристик емпіричного розподілення

Завдання

Характеристик емпіричного розподілення

Приклад обробки статистичних даних і визначення

Для точіння такий розрахунок виконується за наведеними нижче формулами.

Розмірне зношування інструменту на одній заготовці:

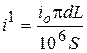, мкм

Запас поля допуску на розмірне зношування різального інструменту:

, мкм

Допустиме розмірне зношування інструмента у межах :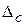

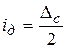, мкм

Число заготовок, що можна обробити без під настроювання технологічної системи:

Величина 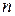округлюється до найближчого меншого цілого числа.

Визначити точність та стабільність операції токарної обробки вала 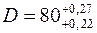мм при випадковій виборці деталей, що оброблені на верстаті при декількох налагодженнях.

1. З метою забезпечення випадковості вибірки деталі, що складають генеральну сукупність, ретельно переміщуємо в тарі, і відбираємо з різних місць тари вибірку для досліджень з кількості – 88 шт.

2. Вимірюємо деталі шкальним інструментом (індикаторною скобою) з ціною поділки с = 0,002 мм. Результати вимірювань заносимо в таблицю 6.5.

Таблиця 6.5 Початкові дані

80,247	80,246	80,235	80,252	80,245	80,257	80,244	80,246
80,250	80,241	80,250	80,240	80,251	80,239	80,249	80,228
80,259	80,253	80,238	80,246	80,264	80,248	80,243	80,253
80,233	80,262	80,247	80,244	80,258	80,255	80,245	80,234
80,242	80,251	80,236	80,249	80,243	80,241	80,256	80,247
80,260	80,245	80,255	80,248	80,247	80,250	80,242	80,252
80,252	80,248	80,231	80,242	80,254	80,236	80,243	80,241
80,239	80,237	80,251	80,256	80,243	80,248	80,254	80,248
80,254	80,242	80,234	80,238	80,253	80,235	80,239	80,244
80,240	80,249	80,244	80,245	80,237	80,249	80,246	80,250
80,251	80,257	80,247	80,252	80,255	80,241	80,258	80,240

За результатами вимірювань визначаємо різницю між найбільшим і найменшим розмірами

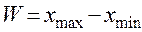= 80,264 – 80,228 = 0,036 мм

3. Отримані значення розбиваємо на 7 інтервалів (d=0,006 мм)

4. Для кожного інтервалу визначаємо частоту, тобто підраховуємо кількість деталей, що увійшли в кожний з інтервалів. Причому в кожний інтервал включаються деталі з розмірами, які лежать в межах від найменшого значення інтервалу включно до найбільшого значення інтервалу, виключаючи його. Отримані дані заносимо в таблицю 6.6.

Таблиця 6.6 Підрахунок частот емпіричного розподілення

Інтервали розмірів	Середина інтервалу xi	Підрахунок частот	Частота ni
від	до
80,225	80,231	80,228
80,231	80,237	80,234
80,237	80,243	80,240
80,243	80,249	80,246
80,249	80,255	80,252
80,255	80,261	80,258
80,261	80,267	80,264
Всього

5. Побудова гістограми та емпіричної кривої розподілення похибок.

Для побудови гістограми розподілення на осі абсцис відкладаємо інтервали розмірів і на кожному з цих інтервалів, як на основі, будуємо прямокутник, висота котрого пропорційна частоті емпіричного розподілення. З’єднуючи середини верхніх сторін прямокутників відрізками прямих, отримуємо графік, який називається емпіричною кривою або полігоном розподілення.(рисунок 6.5)

На основі полігона розподілення похибок в якості гіпотези теоретичного розподілення частот досліджуваного параметра приймаємозакон нормальногорозподілення.

6. Визначення основних параметрів прийнятого закону розподілення.

В якості оцінки основних параметрів закону нормального розподілення використовують вибіркове середнє арифметичне значення досліджуваного параметра 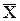і вибіркове середнє квадратичне відхилення S, які обчислюються по формулах (6.24), (6.25):

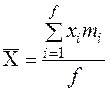
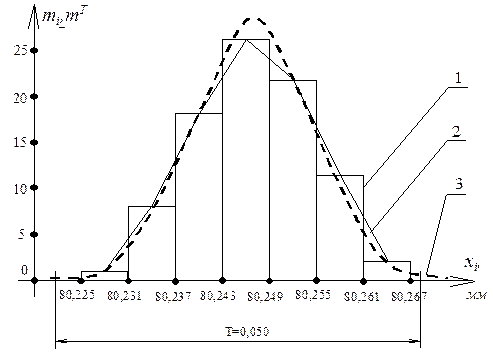
Рисунок 6.5 – Гістограма (1), емпірична крива (2) та теоретична крива

нормального розподілення (3) розмірів деталей

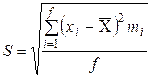
Для полегшення підрахунків використовуємо таблицю 6.7.

Таблиця 6.7 Допоміжна таблиця для обчислення 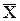і S виборки

Інтервали розмірів	Серед. інтерв. xi	Част. mi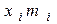
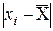
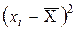
Від	до
80,225	80,231	80,228		80,228	0,019	0,000361	0,000361
80,231	80,237	80,234		641,872	0,013	0,000169	0,001352
80,237	80,243	80,240		1444,32	0,007	0,000049	0,000882
80,243	80,249	80,246		2086,396	0,001	0,000001	0,000026
80,249	80,255	80,252		1765,544	0,005	0,000025	0,00055
80,255	80,261	80,258		882,838	0,011	0,000121	0,001331
80,261	80,267	80,264		160,528	0,017	0,000289	0,000578
Всього		7061,726		0,00508

Вибіркове середнє арифметичне значення :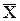

Вибіркове середнє квадратичне відхилення S:

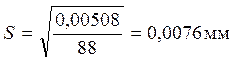
7. Порівняння емпіричного розподілення з теоретичним та побудова теоретичної кривої

По зовнішньому вигляді емпіричної кривої можна приблизно встановити закон розподілення похибок в генеральній сукупності. Для більш точного висновку необхідно співставити емпіричну криву з кривою, що передбачається теоретично. З цією метою для кожного інтервалу значень необхідно обчислити теоретичні частоти або частості і по них побудувати теоретичну криву розподілення.

При побудові теоретичної кривої нормального розподілення приймається, що і .

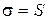Теоретичну частоту обраховуємо по формулі (6.44):

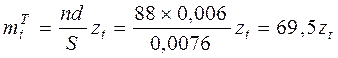(6.44)

Величина 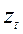обчислена для різних значень t і наведена в додатку 2.1 кафедрального довідника №8. Значення t для кожного інтервалу розмірів знаходяться по формулі (6.45):

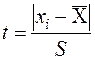(6.45)

Отже, для підрахунку теоретичних частот необхідно для кожного інтервалу розмірів по формулі (6.45) визначити значення t, по кафедральному довіднику - таблицях додатку М2.13 знайти 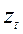i потім скористатися формулою (6.44). При підрахунку теоретичних частот доцільно використати допоміжну таблицю 6.8.

Таблиця 6.8 Обчислення теоретичних частот нормального Розподілення

Інтервали розмірів	Серед. інтерв. xi	Част. mi		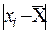t	zt	Теор. част.	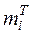Теорет. част. 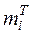(з окр.)
від	до
80,225	80,231	80,228		0,019	2,5	0,0175	1,2
80,231	80,237	80,234		0,013	1,71	0,0925	6,4
80,237	80,243	80,240		0,007	0,92	0,2613	18,2
80,243	80,249	80,246		0,001	0,13	0,3956	27,5
80,249	80,255	80,252		0,005	0,66	0,3209	22,3
80,255	80,261	80,258		0,011	1,45	0,1394	9,7
80,261	80,267	80,264		0,017	2,24	0,0325	2,3
Всього

Для точної побудови теоретичної кривої нормального розподілення обчислюють координати характерних точок кривої нормального розподілення по формулах, і будується таблиця 6.9

Таблиця 6.9 Координати характерних точок кривої нормального розподілення

Характерні точки	Абсциса	Ордината
Вершина кривої		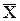80,247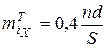
Точка перегину		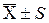80,2546
80,2394
Точка перегину		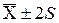80,2622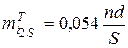
80,2318
Точка перегину		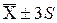80,2698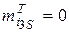
80,2242

Графік теоретичної кривої нормального розподілення поєднати з гістограмою і емпіричною кривою, тобто зобразити на рисунку 6.5.

8. Перевірка гіпотези про розподілення випадкової величини.

Для перевірки відповідності емпіричного розподілення теоретичному існує ряд критеріїв. В даному прикладі з цією метою використовується критерій Пірсона :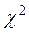

Для зручності обчислення доцільно використати таблицю 6.10.

При визначенні критерію необхідно, щоб частота була не менше п’яти. Якщо в будь-якому інтервалі частота буде менше п’яти, то її слід об’єднати з сусіднім значенням.

Потім необхідно знайти число k по формулі:

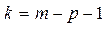
де p – число параметрів теоретичного розподілення. Для нормального розподілення p=2. По таблицях додатку М2.13 кафедрального довідника по знайдених з наченнях 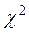і k визначається ймовірність 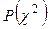. Якщо буде виконуватися нерівність 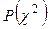> 0.05, то можна вважати, що емпіричній розподіл відповідає теоретичному (нормальному) і можна використовувати його закономірності для аналізу точності обробки.

Якщо вказана нерівність виконуватися не буде, то в якості теоретичного розподілення слід використовувати інший закон розподілу.

Таблиця 6.10 Допоміжна таблиця для обчислення критерію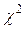

Інтервали розмірів	Середина Інтервалу Xi	Част. mi	Теорет. част.
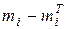
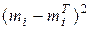
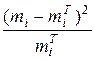
від	до
80,225	80,231	80,228		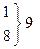			0,125
80,231	80,237	80,234
80,237	80,243	80,240
80,243	80,249	80,246		28	-2		0,143
80,249	80,255	80,252
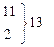
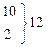
80,255	80,261	80,258					0,083
80,261	80,267	80,264
Всього				0,351

В наведеному прикладі:

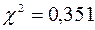; k=5-2-1=2

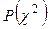=0,8 > 0,05

Відповідно можна вважати, що розподілення розмірів відповідає нормальному закону.

9. Визначення ймовірності проценту браку при виконанні операції, що досліджується.

Для нормального розподілення поле розсіювання похибок (в генеральній сукупності) визначається по формулі:

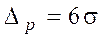
Вибіркове середнє квадратичне відхилення S є наближеною оцінкою середньо квадратичного відхилення випадкової величини . Похибка оцінки по S залежить від об’єму вибірки.

Враховуючи цю обставину, значення визначимо із співвідношення:

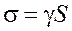
Де 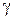- коефіцієнт, який приймається в залежності від об’єму вибірки по таблиці.

Необхідною умовою обробки деталі без браку є виконання двох умов (6.19) та (6.20).

а) перевірка першої умови за (6.29)

;

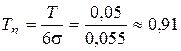б) перевірка другої умови за (6.30)

мм

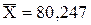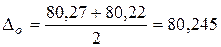де мм

мм

мм

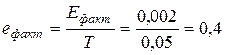
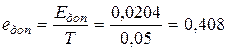
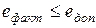
Одна з умов (перша) не виконується, отже – уникнути браку неможливо, необхідно розрахувати величину ймовірного браку.

Якщо задано допуск на розмір і граничні розміри деталі по кресленню x_в і х_н , то ймовірний процент браку складе:

по верхній границі поля допуску:

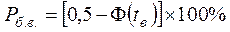
по нижній границі поля допуску:

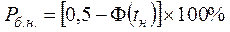
В цих формулах:

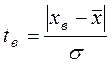
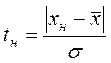
В наведеному прикладі:

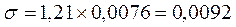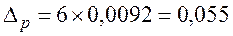мм

мм

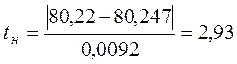
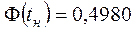
по верхній границі поля допуску (виправний брак):

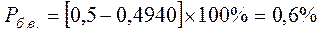
по нижній границі поля допуску (невиправний брак):

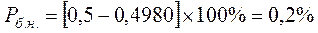
Отже можливий брак становить:

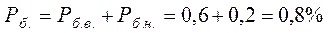
що становить 1 деталь при розмірі вибірки N=88.

Отже точність технологічної операції недостатня і ймовірний процент браку становить 0,8%, процес обробки ненадійний, хоча точність налагоджування виконана правильно.

Технологічний допуск, який можна витримати на даній операції, при обробці деталі без браку згідно першої умови становить:

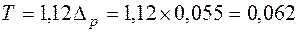мм

Дата добавления: 2014-12-24