Термодинамическая теория флуктуаций

Статистическое определение энтропии.

В 1877 году Людвиг Больцман установил связь энтропии с вероятностью данного состояния. Позднее эту связь представил в виде формулы Макс Планк:

S=k∙ln(W)

где константа k = 1,38×10−23 Дж/К названа Планком постоянной Больцмана, а Ω — статистический вес состояния, является числом возможных микросостояний (способов) с помощью которых можно перейти в данное макроскопическое состояние. Этот постулат, названный Альбертом Эйнштейном принципом Больцмана, положил начало статистической механики, которая описывает термодинамические системы, используя статистическое поведение составляющих их компонентов. Принцип Больцмана связывает микроскопические свойства системы (Ω) с одним из её термодинамических свойств (S).

Рассмотрим, например, идеальный газ в сосуде. Микросостояние определено как позиции и импульсы (моменты движения) каждого составляющего систему атома. Связность предъявляет к нам требования рассматривать только те микросостояния, для которых: (I) месторасположения всех частей расположены в рамках сосуда, (II) для получения общей энергии газа кинетические энергии атомов суммируются.

Согласно определению, энтропия является функцией состояния, то есть не зависит от способа достижения этого состояния, а определяется параметрами этого состояния. Так как Ω может быть только натуральным числом (1, 2, 3, …), то энтропия Больцмана должна быть неотрицательной — исходя из свойств логарифма.

Флуктуации (от лат. fluctuatio – колебание), случайные отклонения наблюдаемых физических величин от их средних значений. Флуктуации происходят у любых величин, зависящих от случайных факторов и описываемых методами статистики (см. Случайный процесс). Количественная характеристика Флуктуации основана на методах математической статистики и вероятностей теории. Простейшей мерой Флуктуации величины х служит её дисперсия s² _x, т.е. средний квадрат отклонения х от её среднего значения 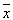, s² _x = ,где черта сверху означает статистическое усреднение. Эквивалентной мерой Флуктуации является квадратичное отклонение Ox, равное корню квадратному из дисперсии, или его относительная величина d _x = s _х/х.

В статистической физике наблюдаемые значения физических величин очень близки к их средним статистическим значениям, т. е. Флуктуации, вызванные случайным тепловым движением частиц (например, Флуктуации средней энергии, плотности, давления), очень малы. Однако они имеют принципиальное значение, ограничивая пределы применимости термодинамических понятий лишь большими (содержащими очень много частиц) системами, для которых Флуктуации значительно меньше самих флуктуирующих величин. Существование Флуктуации уточняет смысл второго начала термодинамики: утверждение о невозможности вечного двигателя 2-го рода остаётся справедливым, но оказываются возможными Флуктуации системы из равновесного состояния в неравновесные, обладающие меньшей энтропией; однако на основе таких Флуктуации нельзя построить вечный двигатель 2-го рода. Для средних величин остаётся справедливым закон возрастания энтропии в изолированной системе.

Основы теории Флуктуации были заложены в работах Дж. Гиббса, А. Эйнштейна, М. Смолуховского.

С помощью Гиббса распределений можно вычислить Флуктуации в состоянии статистического равновесия для систем, находящихся в различных физических условиях; при этом Флуктуации выражаются через равновесные термодинамические параметры и производные потенциалов термодинамических. Например, для систем с постоянным объёмом V и постоянным числом частиц N, находящихся в контакте с термостатом (с температурой Т), каноническое распределение Гиббса даёт для Флуктуации энергии (Е): 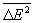= (kT)² C_V, где k – Больцмана постоянная, C_V – теплоёмкость при постоянном объёме. Такое же выражение для Флуктуации справедливо и в случае квантовой статистики, различаются лишь явные выражения для C_V. Для систем с постоянным объёмом в контакте с термостатом и резервуаром частиц большое каноническое распределение Гиббса даёт для Флуктуации числа частиц: 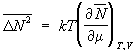, где m – химический потенциал. В приведённых примерах флуктуируют пропорциональные объёму (т. н. экстенсивные) величины. Их относительные квадратичные Флуктуации пропорциональны величине 1/ N (нормальные Флуктуации) и, следовательно, очень малы. В точках фазовых переходов Флуктуации сильно возрастают, и их относительное убывание с N может быть более медленным.

Неравновесные процессы.

Неравновесные процессы в термодинамике (См. Термодинамика) и статистической физике (См. Статистическая физика) — физические процессы, включающие неравновесные состояния (См. Неравновесное состояние). Примеры: процесс установления равновесия (термодинамического или статистического) в системе, находившейся ранее в неравновесном состоянии; переход системы из равновесного состояния в неравновесное или из одного неравновесного состояния в другое под влиянием внешних возмущений. В неизолированных системах Н. п. могут протекать стационарно (без изменения физического состояния системы, пример — Теплопередача теплопроводностью при постоянной разности температур). Н. п. являются необратимыми процессами (См. Необратимые процессы), связанными с производством энтропии (См. Производство энтропии).

Дата добавления: 2014-12-24