Вязкость

Вязкость является одной из важных характеристик жидкостей и газов. Вязкость нефтепродуктов определяет их подвижность в условиях эксплуатации двигателей, машин и механизмов, существен­но влияет на расход энергии при транспортировании, фильтрации, перемешивании. Вязкость определяет способность жидкости и газа сопротивляться взаимному перемещению их частиц. Вязкость характеризуется коэффициентом внутреннего трения (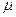), или коэффициентом динамической вязкости, называемым также динамической вязкостью. Коэффициент динамической вязкости 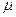зависит от природы жидкости (газа) и температуры. Единица динамической вязкости в системе СИ - паскаль×секунда (Па×с). Для выражения динамической вязкости целесообразно применять дольную единицу - миллипаскаль-секунда (мПа×с).

В нефтепереработке наиболее широко пользуются понятием кинематической вязкости. Кинематической вязкостью (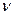) называется отношение динамической вязкости к плотности данной жидкости или газа при той же температуре

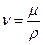(38)

Следовательно, в СИ единицей измерения кинематической вязкости является v = 1м²/с.

Для практической характеристики нефтепродуктов пользуются условной вязкостью (измеряемой в градусах ВУ - °ВУ), под которой понимают отношение длительности истечения 200мл испытуемого нефтепродукта из стандартного вискозиметра при температуре испытания к длительности истечения того же количества дистиллированной воды при 20°С. Условную вязкость пересчитывают в кинематическую по таблице (Приложение 17). Для перевода больших значений вязкости (выше 16°ВУ) рекомендуется пользоваться формулой

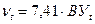(39)

где 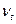- кинематическая вязкость при температуре t, мм²/с; ВУ_t - условная вязкость при той же температуре, °ВУ.

При выполнении технологических расчетов часто приходится пересчитывать вязкость с одной температуры на другую. Для этой цели предложен ряд формул, но наиболее широко пользуются номограммой, приведенной в Приложении 13. Пользование номограммой объяснено в Примере 20.

Пример 17. Условная вязкость масляной фракции при 50 и 100°С соответственно 20,1 и 2,26°ВУ. Какова кинематическая вязкость масляной фракции при тех же температурах.

Решение. По таблице (Приложение 17), находим, что вязкости 2,26°ВУ соответствует =14 мм²/с. Условную вязкость при 50°С переведем в кинематическую, используя формулу (39)

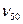= 7,4l × 20,l = 149 мм²/с

Пример 18. Условная вязкость масляной фракции при 100 и 50°С соответственно 2,6 и 20°ВУ. Определить по графику (Приложение 13) условную вязкость при 70°С.

Решение. На графике определяем положение точек, соответствующих данным значениям условной вязкости. Для этого из точек, соответствующих 100 и 50°С и расположенных на оси абсцисс, проводим две вертикальные прямые до пересечения каждой с горизонтальной прямой, проведенной из точки, соответствующей условной вязкости. Получаем на номограмме две точки пересечения А и В, через которые проводим прямую АВ, дающую зависимость вязкости от температуры для данной фракции. На оси абсцисс находим точку, соответствующую 70°С, из которой восстанавливаем перпендикуляр до пересечения с прямой АВ. Получаем точку С и из этой точки проводим горизонталь до пересечения со шкалой условной вязкости. Получаем значение ВУ = 7,1.

Многим смазочным маслам приходится работать в широком диапазоне температур. Чем меньше меняется вязкость масла с изменением температуры, тем более качественным оно считается. Зависимость вязкости масел от температуры принято характеризовать различными вязкостно-температурными константами: отношением вязкости при двух температурах, индексом вязкости, вязкостно-массовой константой и др.

Характер изменения вязкости при изменении температуры принято определять отношением кинематической вязкости при 50°С к кинематической вязкости при 100°С. Отношение вязкостей при двух температурах является приближенной мерой оценки измене­ния крутизны вязкостной кривой в заданном интервале температур.

Одной из характеристик, показывающих зависимость вязкости масел от температуры, является условная константа - индекс вяз­кости (ИВ). Индекс вязкости находят по графикам, один из которых приведен в Приложении 14. Методика пользования графиком пояснена схемой в правом углу чертежа. Из этой схемы видно, что определение ИВ сводится к соединению прямыми известных величин кинематической вязкости 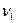, при двух температурах t₁, t₂ и продолжению этих прямых до взаимного пересечения. Точка пересечения и определяет искомый ИВ.

В литературе описывается ряд формул, в основном эмпирических, характеризующих изменение вязкости жидкостей в зависимости от температуры. Приведем некоторые из них.

Формула Дина и Лана, которую представим в следующем виде:

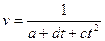(40)

Формула В. Гершеля:

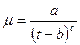(41)

Широко распространенная для нефтепродуктов эмпирическая формула Вальтера:

lglg (v + c) = a + blgT (42)

В этих уравнениях t и Т - температура соответственно в °С и °К;

ν и μ - кинематическая и динамическая вязкости при данной температуре;

а, b и с - постоянные, зависящие от природы исследуемой жидкости.

Постоянные a, b и с могут быть подсчитаны, если для данного продукта известны три экспериментальные точки, т. е. значения вязкостей для каких-либо трех температур. Подставив эти значения в любую из указанных выше формул, получим для каждой формулы три уравнения с тремя неизвестными, ре­шив которые и определяют постоянные a, b и с.

Более удобны для практического использования, но менее точны формулы, в которые входят только две постоянные; этими формулами можно пользоваться при наличии только двух экспериментальных точек.

К таким формулам относятся:

1) формула С. А. Гросса, применяемая для нефтепродуктов при повышенных температурах или малых вязкостях

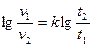(43)

тождественная уравнению

lg v = a - blgt (44)

при температурах 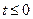°С формула Гросса теряет смысл, так как уже при t = 0°C lg 0 = -∞;

2) формула Филонова для нефтепродуктов при низких температурах (или высоких вязкостях):

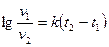(45)

тождественная уравнению

lg v = a - bt (46)

Здесь постоянные для данного нефтепродукта коэффициенты k в формулах (43) или (44) или а и b в формулах (44) или (46) могут быть найдены по двум экспериментальным точкам.

Формулу Вальтера (42) обычно также упрощают для возможности ее применения на основе двух экспериментальных точек. При этом учитывают, что коэффициент с в уравнении (42), если выражать вязкость в сантистоксах, имеет максимальное значение около 1,3 (для бензинов) и минимальное - порядка 0,5 (для некоторых высоковязких нефтепродуктов). Исходя из изложенного, для всех нефтепродуктов (нефтей, смазочных масел) при вязкостях более 2-5 ccт в формуле (42) обычно применяют усредненное значение с = 0,8:

lglg (ν + 0,8) = a + blgT (47)

При малых вязкостях последняя формула неприменима, так как при ν 0,2 cст уравнение вообще теряет смысл.

Г. Конгейм и др. предлагают для нефтепродуктов в области малых вязкостей (примерно ниже 10 cст) принимать с = 1,22.

Для облегчения расчетов по формуле (42) с тем или иным значением коэффициента с строят специальные номографические сетки (приложение 12), в которых ось абсцисс разделена пропорционально lgT, а ось ординат - пропорционально lglg(ν + c), где Т в К, a ν в cст. Предполагается, что в построенной таким путем сетке линии температурной зависимости вязкости нефтепродуктов являются прямыми. Эти прямые для каждого продукта наносят по двум или нескольким известным экспериментальным точкам.

Формулу (42) и построенные на ее основе номограммы для нефтепродуктов используют в широких пределах температур (примерно от -50 до +250°С) и вязкостей (от нескольких десятых долей до нескольких миллионов сантистокс). Температурные условия должны быть ограничены, с одной стороны, тем, чтобы продукт не был близок к застыванию (оставался жидким), а с другой, - чтобы он не был близок к состоянию кипения.

Формула Вальтера и соответствующая ей сетка могут быть использованы и для некоторых других веществ - глицерина, продуктов разгонки каменноугольной смолы, животных и растительных жиров, в том числе касторового масла. Номограммы, построенные на базе формулы Вальтера в достаточно крупном масштабе, позволяют применять их для практических расчетов.

Пример 19. Нефтяная фракция, выкипающая в пределах 225 - 250°С, имеет при температуре t₁ = 10°С кинематическую вязкость ν₁ = 3,96×10^-6м²/сек = 3,96сст, а при t₂ = 80°С соответственно ν₂ = 1,21×10^-6м²/сек = 1,21cст.

Требуется:

а) на базе формулы Вальтера (47) установить для указанной выше фракции уравнение зависимости вязкости от температуры;

б) подсчитать вязкость фракции при температурах 0, 50 и 100 С.

Решение: а) Напишем формулу (47) для двух температур Т₁ и Т₂:

lg lg(ν₁ + 0,8) = a + blgT₁;

lg lg(ν₂ + 0,8) = a + blgT₂.

Решая эти уравнения совместно, находим:

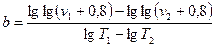(48)

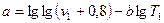(49)

Для t₁ = 10°С и ν₁ = 3,96сст имеем:

T₁ 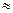283,1К; lg T₁ = 2,4520;

lg lg (ν₁ + 0,8) = lg lg 4,76 = lg 0,6776 =1,8310 = - 0,1690.

Для t₂ = 80°C и ν₂ = l,21 cст имеем:

T₂ 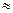353,1К; lg T₂ = 2,5479;

lg lg (ν₂ + 0,8) = lg lg 2,01 = lg 0,3032 = 1,4817 = - 0,5183.

Следовательно, из выражения (48) находим:

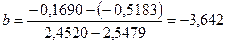
При помощи уравнения (49) получаем:

а = - 0,1690 - (-3,642) 2,4520 = 8,763.

Подставив значения а и b в формулу (47), находим искомое уравнение температурной зависимости вязкости для данной фракции:

lg lg (ν + 0,8) = 8,763 - 3,642 lg T. (50)

б) подставив в полученную формулу (50) значение температуры t = 0°С 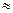273,1К, получим:

lg lg (ν₀ + 0,8) = 8,763 - 3,642 lg 273,1 = - 0,112 =1,888,

откуда

lg(ν_o + 0,8) = 0,7727,

или

ν₀ +0,8 = 5,926.

Следовательно, ν_o 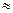5,13 сст = 5,13×10^-6 м²/сек.

Аналогично находим для температур t = 50°С и t = 100°С значения

ν₅₀ = 1,83 · 10^-6 м²/сек и ν₁₀₀ = 0,974 · 10^-6 м²/сек.

Экспериментально для данной фракции было найдено (в м²/сек):

ν₀ = 5,23 · 10^-6, ν₅₀ = 1,79 · 10^-6 и ν₁₀₀ = 0,987 · 10^-6.

Как видим, для рассматриваемой фракции и при интерполяции (ν₅₀), и при экстраполяции (ν₀ и ν₁₀₀) ошибки не превышают 2%, что для техноло­гических расчетов вполне приемлемо.

Пример 20. Используя исходные данные, приведенные в примере 19. подсчитать вязкость фракции при t = 50°С с помощью формулы (43) Гросса.

Решение. Из формулы (43):

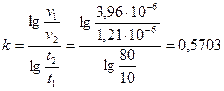
Принимая в формуле (43) в качестве постоянной, например, вторую точку (t₂ = 80°С и ν₂ = 1,21 · 10^-6 м²/сек), получим уравнение температурной зависимости для данной фракции:

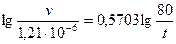(51)

которое при желании можно привести и к виду (44).

Подставив заданную температуру t = 50°С, находим;

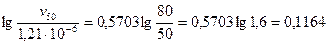
откуда

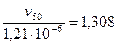
или

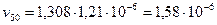м²/сек

В данном случае ошибка по сравнению с экспериментально найденным значением ν₅₀ = 1,79 · 10^-6 м²/сек составляет довольно значительную величину - минус 11,7%.

С повышением давления вязкость жидкости возрастает: до 250 атмосфер почти прямо пропорционально давлению, а затем более быстро.

При небольших давлениях вязкость жидких продуктов можно вычислить по формуле

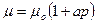(52)

где μ₀ - динамическая вязкость при 760 мм рт. ст. (1,01325бар);

р - избыточное давление в ат;

α 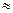0,001 - постоянная.

Температурную зависимость вязкости, как и некоторых других свойств жидкости, можно установить путем сравнения данной жидкости с какой-либо другой, по возможности родственной по своей природе жидкостью, называемой эталонной или стандартной. Для этого можно использовать закон линейности химико-технических функций К. Ф. Павлова, который в общем виде выражается формулой

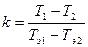(53)

где Т₁ и Т₂ - две температуры, для которых значения μ₁ и μ₂ какого-либо свойства, например вязкости, исследуемой жидкости известны;

Т_э1 и Т_э2 - температуры эталонного вещества, отвечающие тем же значениям μ₁ и μ₂ рассматриваемого свойства;

k - постоянная для данной пары жидкостей.

Вязкость не является аддитивным свойством. Текучесть, т. е. величину, обратную вязкости, с некоторым приближением можно считать свойством аддитивным. Однако наиболее надежным путем для установления вязкости смеси является экспериментальное определение. Если опытным путем найдена вязкость смеси при двух-трех температурах, можно подсчитать вязкость смеси при других температурах, используя приведенные выше формулы температурной зависимости вязкости.

Предложен ряд формул, графиков и таблиц для подсчета вязкости смесей. Надо иметь в виду, что все они дают более или менее удовлетворительные результаты только для случаев, когда смесь составлена из компонентов, близких по свойствам, или взятых примерно в одинаковых количествах; в противном случае точность снижается.

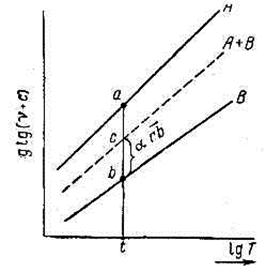
Рис. 10. Построение на номографической сетке Вальтера линии А + В

зависимости кинематической вязкости смеси от температуры при а = const.

а — массовая доля компонента А в смеси.

Предположим, что из двух нефтепродуктов А и В приготовлена их смесь А + В, в которой массовую долю компонента А обозначим через а. Пусть далее на номограмме-сетке, построенной на базе формулы (42), нанесены прямые температурной зависимости вязкости для обоих смешиваемых компонентов (рис. 10, прямые А и В). Можно сделать допущение, что прямая А + В вязкости смеси будет расположена между прямыми А и В на расстояниях, обратно про­порциональных содержанию этих компонентов в смеси. Для ординаты, отвечающей любой температуре t, отрезок ab, заключенный между линиями А и В, будет делиться на две част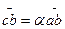и:

и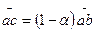

Номограмму-сетку, построенную на базе формулы (42), можно использовать также для построения линии вязкости ν_AB смеси компонентов А и В при заданной температуре t в зависимости от α - процентного содержания в смеси компонента А, т. е. линии ν_AB = f(a), при t = const.

Так как шкала температур, на участке от 0 до 100°С близка к равномерной, то этот участок принимают за шкалу a изменения от 0 до 100% содержания компонента А в смеси (рис. 11). Тогда, отложив на ординате, отвечающей α = 0%, точку В (вязкость ν_В) для одного компонента, а на ординате α = 100% точку А (вязкость ν_А) для другого компонента и соединив эти точки прямой, получают искомую линию АВ, отвечающую уравнению ν_AB = f(α). Здесь ν_A, ν_B и ν_AB - кинематические вязкости компонентов и их смеси, взятые при одинаковой заданной температуре.

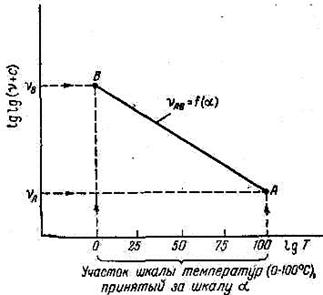
Рис. 11. К использованию номографиче­ской сетки Вальтера

для установления зависимости вязкости смеси (ν_AB)

от массовой доли а компонента

А в смеси при t = const

Изложенный выше графический метод определения вязкости смеси жидких нефтепродуктов может быть заменен аналитическим. При этом используют выражение:

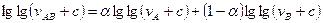(54)

где ν_A, ν_B и ν_AB -вязкости при одинаковой температуре в сст;

α - массовая доля компонента А в смеси А + В;

с - коэффициент к формулам (42) и (47).

Пример 21. Нефтепродукт А вязкостью ν_A = 20сст смешивается с про­дуктом В, вязкость которого ν_В = 40сст. Найти вязкость их смеси, в кото­рой содержание компонента А составляет α = 65% масс.

Решение. Используем формулу (54) с коэффициентом c = 0,8;

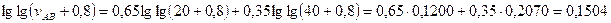
откуда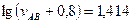

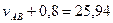
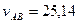ccт.

Вязкость суспензий с концентрацией твердой фазы менее 10% объемн. можно рассчитать по формуле Бачинского:

m_с = m_ж (1 + 4,5 j) (55)

где m_с и m_ж – динамическая вязкость суспензии и чистой жидкости;

j - объемная концентрация (в долях) твердой фазы в суспензии.

Вязкость эмульсий можно подсчитать по формуле:

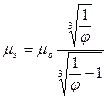(56)

где m_э и m_о – динамическая вязкость эмульсии и чистой сплошной фазы;

j - объемная доля взвешенной фазы.

Для газов и паров приведем следующие наиболее распространенные формулы, устанавливающие зависимость вязкости от температуры:

Сатерлэнда 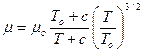(57)

Фроста 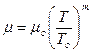(58)

Здесь m и m₀ – динамическая вязкость газа при температурах Т и Т₀ (К) и заданном давлении. Обычно принимают Т₀ = 273,15К;

c и m – параметры, которые могут быть подсчитаны по опытным данным, если кроме m_о известна еще одна точка (т.е. m при любом значении Т).

Параметры с и m принято считать за постоянные, причем Фрост считает возможным для большинства случаев принимать m» 1. Однако m и особенно с зависят от выбора экспериментальной точки для их определения.

Значения c и m можно найти в справочной литературе.

Можно рекомендовать также следующие две формулы Фроста:

а) вязкость паров алканов, алкенов и цикланов, а также их смесей:

m = Т (6,5 – 2,25 × lgМ) × 10^-8 (59)

б) то же для смесей паров ароматических углеводородов и цикланов с парами алканов, алкенов и алкинов (т.е. практически для смесей всех видов углеводородов):

m = Т (6,6 – 2,25 × lgМ) × 10^-8 (60)

В последних двух формулах:

Т – температура в К;

М – молекулярный вес углеводородов или их смесей;

m - динамическая вязкость в н × сек/м².

С повышением давления динамическая вязкость газов и паров возрастает. Н.Б. Варгафтик предложил для широкого интервала давлений следующее эмпирическое уравнение:

m_р = m_о + А × rⁿ (61)

где m_р и m_о – динамическая вязкость газа соответственно при давлениях р и р_о = 760 мм рт. ст.;

r - плотность газа при давлении р;

А и n – постоянные, определяемые опытным путем (по двум известным точкам).

При небольших давлениях (порядка 5-10 бар) влиянием давления на вязкость газов и паров можно пренебречь.

Для подсчета кинематической вязкости смеси газов часто используется приближенная формула Манна:

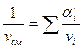(62)

где v _i – кинематическая вязкость отдельных компонентов газовой смеси;

v _см - то же для смеси;

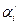- мольные (или объемные) доли компонентов.

Пример 22. Определить кинематическую вязкость паров н -пентана при атмосферном давлении и температуре t = 100⁰С.

Решение. Для паров нормального пентана при 760 мм рт. ст. (1,01325 бар) и 0⁰С имеем: m₀ = 6,355 н × сек/м² = 6,355 кг/м × сек; m = 0,99 и r₀ = 3,457 кг/м³. Необходимо иметь в виду, что при 0⁰С и атмосферном давлении н -пентан фактически находится в жидком состоянии, поэтому приведенные выше значения m₀ и r₀ являются лишь условными расчетными параметрами. Однако значение m₀ действительно для паров н -пентана при 0⁰С и давлении, меньшем чем атмосферное, так как давление мало влияет на величину динамической вязкости паров.

Применяя формулу (58), находим для t = 100⁰С:

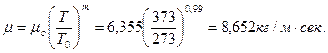
Плотность паров н -пентана при 100⁰С подсчитаем имея в виду, что р = р₀» 1,013 бар:

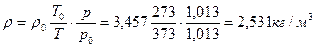
Найдем искомое значение кинематической вязкости:

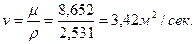
В практике широко пользуются также номограммой, приведенной в Приложении 15. Используя эту номограмму, можно определить вязкость смеси двух нефтепродуктов различной вязкости при данной температуре и смешанных между собой в определенном отношении, а также определить соотношение компонентов в смеси для получения продукта определенной вязкости при данной температуре.

Пример 23. Смесь составлена из компонентов А и В. Для компонента А ВУ₅₀ = 2,2. Для компонента В ВУ₅₀ = 9. Определить:

1) вязкость при 50 °С смеси, состоящей из 40% объемн. компонента A и 60% объемн. компонента В; 2) соотношение в смеси компонентов А и В, при котором вязкость условная смеси ВУ₅₀ = 5,9.

Решение. Для определения вязкости смеси построим линию зависимости вязкости смеси от соотношения компонентов. Для этого отложим на ординате, отвечающей 100% компонента А (Приложение 15), точку т, соответствующую вязкости ВУ₅₀= 2,2, а на ординате, отвечающей 100% компонента В, точку п, соответствую­щую вязкости ВУ₅₀ = 9. Соединив эти точки, получим прямую тп, характеризующую зависимость вязкости смеси от концентрации компонентов. Теперь можно ответить на оба вопроса: 1) отложим на абсциссе точку, соответствующую 40% компонента А (и 60% компонента В), и восстановим перпендикуляр до пересечения с прямой тп, получив на ординате точку, которая показывает, что вязкость данной смеси ВУ = 4,3 (на графике - сплошная линия); 2) смесь с ВУ=5,9 состоит из 25% компонента А и 75% компонента В (на графике -пунктирная линия).

Вязкостно-массовая константа (ВМК) устанавливает связь между вязкостью и плотностью, но так как по плотности можно в некоторой степени судить о химическом составе нефтепродукта, то ВМК дает косвенную зависимость между вязкостными и химическими свойствами минеральных смазочных масел. Для определения ВМК предложен ряд формул, но наиболее широко ис­пользуют зависимость, предложенную Ю. А. Пинкевичем

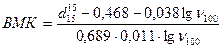(63)

где ВМК - вязкостно-массовая константа; 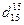-относительная плотность нефтепродукта; - кинематическая вязкость нефтепродукта при 100°С, мм²/с:

Для высококипящих фракций нефти ВМК изменяется в пределах 0,75-0,90. Чем больше значение ВМК, тем ниже вязкостно-температурные качества масел.

Задача 24. Условная вязкость масляной фракции при 50 и 100⁰С соответственно ⁰В У₅₀ и ⁰В У₁₀₀. Какова кинематическая вязкость масляной фракции при тех же температурах?

параметры	Варианты
^0В У50
^0В У100		3,81	3,63	3,46	3,22	3,02	2,81	2,6	2,42	2,2

Задача 25. Условная вязкость масляной фракции при 100 и 50⁰С соответственно ⁰В У₅₀ и ⁰В У₁₀₀. Определить по графику (Приложение 13.) условную вязкость при t⁰С.

параметры	Варианты
^0В У50
^0В У100		2,2	2,4	2,6	2,8		3,2	3,4	3,6	3,8
t^0С

Задача 26. Нефтяная фракция, выкипающая в пределах t_H-t_K⁰C имеет при t₁ кинематическую вязкость ν₁ (м²/сек), а при t₂⁰С соответственно ν₂ (м²/сек).

Установить на базе формулы Вальтера для указанной фракции уравнение зависимости вязкости от температуры.

Подсчитать вязкость фракции при температурах t₃, t₄, t₅ по полученному уравнению.

параметры	Варианты
	объемный состав газа w % объем
tН ^0С
tК ^0С
t1 ^0С
t2 ^0С
ν1 ×10 ^-6 м^2/сек	3,96	3,99	4,31	4,5	4,72	4,76	5,01	5,13	5,21	5,4
ν2×10^-6 м^2/сек	1,03	1,12	1,25	1,37	1,96	2,21	2,34	2,43	2,68	2,87
t3 ^0С
t4 ^0С
t5 ^0С

Задача 27. Нефтепродукт А вязкостью ν_А смешивается с продуктом В, вязкость которого ν_В. Найти вязкость их смеси, в которой содержание компонента А составляет d. Принять с = 0,8.

параметры	Варианты
νА (сст)
νВ (сст)
α

Задача 28. Определить кинематическую вязкость паров углеводорода при давлении Р и температуре t. Принять m = 0,99.

параметры	Варианты
р мм рт.ст.
t ^0С
μ0×10^7 н×сек/м^2
ρ0 кг/(м^3) (0^0С)	0,717	1,357	2,019	3,457	1,173	1,260	3,480	0,717	1,357	2,019

Задача 29. Смесь составлена из компонентов в А и В. Известны для компонентов А ⁰ВУ₅₀ и В ⁰ВУ₅₀. Определить: 1) вязкость при t⁰С смеси состоящей из w% компонентов А и В; 2) соотношение в смеси компонентов А и В при котором вязкость условная смеси ⁰ВУ₅₀.

параметры	Варианты
А ВУ50		2,1	2,2	2,3	2,4	2,5	2,6	2,7	2,8	2,9
В ВУ100		8,5		9,5		10,5		11,5	12,	12,5
А w%
В w%
ВУ50	3,5		4,5		5,5		6,5		7,5

Дата добавления: 2014-12-24