
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формулы для вычислений. Понятие о выборочном наблюдении и его задачи
|
|
|
|
Понятие о выборочном наблюдении и его задачи. Виды выборок. Ошибки выборки. Доверительная вероятность. Определение необходимого объема выборки. Оценка результатов выборочного наблюдения и распространение их на генеральную совокупность.
Тема 5. Выборочное наблюдение
Выборочное наблюдение проводится в тех случаях, когда проведение сплошного наблюдения невозможно или экономически нецелесообразно. Например, проверка качества отдельных видов продукции может быть связана с ее уничтожением, а некоторые совокупности настолько велики, что физически не возможно собрать данные в отношении каждого из их членов. Также выборочное наблюдение используют для проверки результатов сплошного наблюдения.
Выборочной совокупностью называют ту часть единиц, которые отобраны для наблюдения а генеральной - всю совокупность единиц, из которых производится отбор 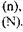
Качество результатов выборочного наблюдения зависит от того, насколько состав выборки представляет генеральную совокупность, т.е., насколько выборка репрезентативна. Для обеспечения репрезентативности выборки необходимо соблюдение принципа случайности отбора единиц.
Методы отбора единиц в выборочную совокупность подразделяют на повторный и бесповторный
При повторном отборе каждая попавшая в выборку единица возвращается в генеральную совокупность и имеет шанс вторично попасть в выборку. При этом вероятность попадания в выборочную совокупность для всех единиц генеральной совокупности остается одинаковой.
Бесповторный отбор означает, что каждая отобранная единица не возвращается в генеральную совокупность и не может подвергнуться вторичной регистрации, а поэтому для остальных единиц вероятность попадания в выборку увеличивается.
Бесповторный отбор дает более точные результаты по сравнению с повторным, т.к. при одном и том же объеме выборки наблюдение охватывает больше единиц генеральной совокупности.
При формировании выборочной совокупности используют следующие виды (способы) отбора: простой случайный отбор; механический отбор; серийная, расслоенная (типическая или стратифицированная), многоступенчатая, многофазовая и моментная выборки.
Случайный отбор производится с помощью жеребьевки либо по таблице случайных чисел. В первом, случае всем элементам генеральной совокупности присваивается порядковый номер и на каждый элемент заводится жребий в виде пронумерованных шаров или карточек-фишек, которые перемешиваются и помещаются в ящик. Затем производится отбор «наудачу». Во втором случае из специальных таблиц производится выбор случайных чисел, которые образуют порядковые номера для отбора. Например, имеется ряд чисел: 60280, 88925. 99610. Применение комбинации этих чисел зависит от размера совокупности: если в ней 1000 единиц, то порядковый номер каждой единицы должен состоять из трех цифр от 000 до 999. В этом случае приведенный ряд чисел даст пять первых номеров единиц выборочной совокупности: 602,808, 892, 599, 610. Остальные номера получают аналогично до тех пор, пока не будет получен заданный объем выборочной совокупности.
При механическом способе отбирается каждый 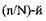 элемент гене-
элемент гене-
ральной совокупности. Например, если имеется совокупность из 100 тыс. единиц и требуется выборка в 1000 единиц, то в нее попадет каждый сотый элемент. Если единицы совокупности не ранжированы относительно изучаемого признака, то 1 -й элемент выбирается наугад, произвольно, а если ранжированы - то из середины 1-й сотни.
При серийном способе в порядке случайной или механической выборки отбирают не единицы, а определенные районы, серии (гнезда), внутри которых проводится сплошное наблюдение.
Расслоенным (стратифицированным) способом производится отбор единиц из неоднородной совокупности. Для этого генеральную совокупность с помощью типологической группировки разбивают на однородные группы, а затем из каждой группы случайным или механическим способом отбирают единицы в выборочную совокупность. При этом единицы разных групп включаются в выборку пропорционально их численности в генеральной совокупности.
| Показатель | Формула |
| общее число единиц единицы, обладающие каким-либо признаком доля единиц, обладающих этим признаком доля единиц, не обладающих этим признаком средняя величина признака дисперсия признака повторный отбор: средняя ошибка доли средняя ошибка признака предельная ошибка доли предельная ошибка признака бесповторный отбор: средняя ошибка доли средняя ошибка признака предельная ошибка доли предельная ошибка признака перенос выборочных характеристик на генеральную совокупность численность выборки повторный отбор бесповторный отбор | N; n
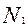 ; m ; m
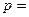 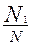 ; ; 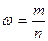 (1-р);
(1-р); 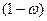
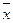 ; ; 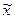
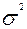 ; ; 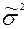
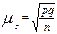 ; ; 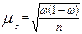
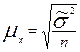 ; ; 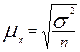
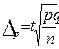 ; ; 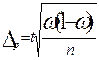
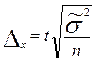 ; ; 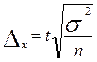
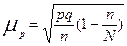 ; ; 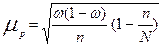
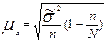 ; ; 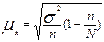
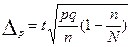 ; ; 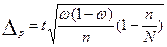
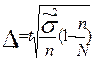 ; ; 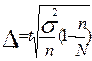
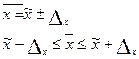 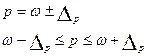
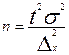 ; ; 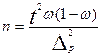 ; ; 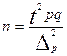
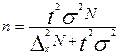 ; ; 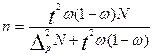
|
Задача 1.
Имеется информация о выпуске продукции (работ, услуг), полученной на основе 10% выборочного наблюдения по предприятиям области:
| Группы предприятий по объему продукции, тыс. руб. | Число предприятий (f) |
| До 100 100-200 200-300 300-400 400-500 500 и > | |
| итого |
Определить: 1) по предприятиям, включенным в выборку: а) средний размер произведенной продукции на одно предприятие; б) дисперсию объема производства; в) долю предприятий с объемом производства продукции более 400 тыс. руб.; 2) в целом по области с вероятностью 0,954 пределы, в которых можно ожидать: а) средний объем производства продукции на одно предприятие; б) долю предприятий с объемом производства продукции более 400 тыс. руб.; 3) общий объем выпуска продукции по области.
Задача 2.
По результатам контрольной проверки налоговыми службами 400 бизнес-структур, у 140 из них в налоговых декларациях не полностью указаны доходы, подлежащие налогообложению. Определите в генеральной совокупности (по всему району) долю бизнес-структур, скрывших часть доходов от уплаты налогов, с вероятностью 0,954.
Задача 3.
Для изучения экономической активности населения района из 200 000 человек методом случайного бесповторного отбора опрошено 4 000 человек. Из них 1 600 человек вложили свои ваучеры в инвестиционные фонды или акции предприятий. С вероятностью 0,954 определить пределы населения всего района, в которых находиться доля экономически активного населения района.
Задача 4.
Для определения средней величины заработной платы работников малых предприятий необходимо провести выборочное обследование методом случайного повторного отбора. Какое количество работников нужно отобрать, чтобы ошибка выборки с вероятностью 0,954 не превышала 2 тыс. руб. при среднем квадратическом отклонении 10 тыс. руб.
|
|
|
|
|
Дата добавления: 2014-12-25; Просмотров: 864; Нарушение авторских прав?; Мы поможем в написании вашей работы!