Полосовые фильтры

Фильтры верхних частот

Используя логарифмическое представление, можно перейти от нижних частот к верхним, зеркально отобразив амплитудно-частотную характеристику коэффициента передачи относительно частоты среза, т.е. заменив  на 1/ или S на 1/ S. При этом частота среза остается без изменения, а K ₀ переходит в K _беск. Из выражения (13) при этом получим

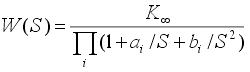
Аналогично, путем замены переменных, можно преобразовать амплитудно-частотную характеристику фильтра нижних частот в амплитудно-частотную характеристику полосового фильтра. Для этого в передаточной функции фильтра нижних частот необходимо произвести следующую замену переменных:

.

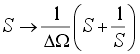(15)

В результате такого преобразования АЧХ фильтра нижних частот в диапазоне 0 1 переходит в правую часть полосы пропускания полосового фильтра (1_макс). Левая часть полосы пропускания является зеркальным отображением в логарифмическом масштабе правой части относительно средней частоты полосового фильтра  = 1. При этом _мин = 1/_макс. Рис. 16 иллюстрирует такое преобразование.

Рис. 16. Преобразование нижних частот в полосу частот

Нормированная ширина полосы пропускания фильтра =_макс–_мин может выбираться произвольно. Из рис. 16 видно, что полосовой фильтр на частотах _макс и _мин обладает таким же коэффициентом передачи, что и ФНЧ при  = 1. Если параметры ФНЧ нормированы относительно частоты среза, на которой его коэффициент передачи уменьшается на 3 дБ, то значение  также будет нормированной шириной полосы пропускания. Учитывая, что

 =_макс–_мин и _макс_мин=1,

получим выражение для вычисления нормированных частот среза полосового фильтра, на которых его коэффициент передачи уменьшается на 3 дБ:

.

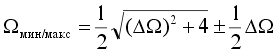Избирательный (селективный) фильтр предназначен для выделения из сложного сигнала монохромной составляющей и по сути является узкополосным полосовым фильтром. Фильтры этого типа имеют АЧХ, подобные амплитудно-частотным характеристикам колебательных LC-контуров. Характерным для этих фильтров является пик АЧХ в области резонансной частоты f _р. Характеристикой избирательности фильтра является добротность Q, определяемая как отношение резонансной частоты к полосе пропускания, т.е.

Q = f p/(f макс – f мин) = 1/(макс –мин) = 1/.

(16)

Простейший полосовой фильтр можно получить, применив преобразование (15) к передаточной функции ФНЧ первого порядка (10). В результате получим:

.

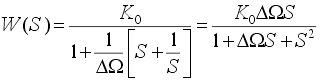(17)

Подставив выражение для добротности (16) в соотношение (17), получим передаточную функцию полосового фильтра

.

(18)

Это выражение дает возможность определить основные параметры полосового фильтра второго порядка непосредственно из его передаточной функции.

Дата добавления: 2014-12-25