Середня квадратична

Застосовується для визначення середніх сторін квадратів, середніх діаметрів циліндричних тіл.

Проста Зважена

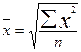
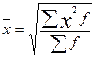
Позначення ті ж, що і в попередніх формулах середніх величин.

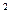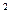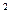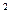Приклад 4 Маємо два квадрати зі сторонами 20 і 30 см. Треба визначити середню сторону квадрата. Середня арифметична цих величин – 25 см. не відповідає дійсності. Площа двох квадратів з такою стороною дорівнює 1250см (25 *2), а дійсна площа 1300 м (20 +30 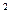). Знаючи площу двох квадратів (1300 см 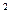), можна визначити сторону рівновеликого квадрата. Вона буде дорівнювати кореню квадратному із половини загальної площі.

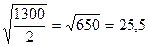см.

Цей же результат дає і середня квадратична.

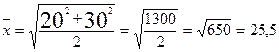см.

Структурні середні (мода і медіана)

Модою в статистиці називається ознака, що зустрічається в досліджуваній сукупності найбільш часто. Для дискретного ряду розподілу модою буде ознака, що має найбільшу частоту (f). В інтервальному ряді розподілу мода обчислюється за формулою:

,

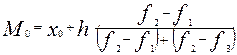де 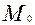- мода (конкретне значення);

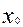- мінімальне значення модального інтервалу;

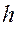- величина модального інтервалу;

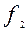- частота модального інтервалу;

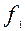- частота інтервалу, що стоїть перед модальним;

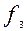- частота інтервалу, що стоїть після модального.

Медіаною називається ознака, яка знаходиться в середині ранжированого ряду значень ознаки. Медіана в інтервальному ряду розподілу обчислюється за формулою

,

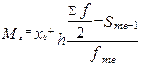де 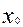- мінімальне значення медіанного інтервалу;

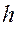- величина медіанного інтервалу; 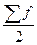- напівсума частот;

S me-1 - сума частот, що стоять перед медіанною частотою;

f me - частота медіанного інтервалу.

Приклад 5: Маємо такі дані про розподіл магазинів за обсягом товарообігу.

Товарооборот тис. грн. Х	Кількість магазинів	Середина інтервалу	Накопичення частоти
f	Xі	f me
1833-1851
1851-1869
1869-1887
1887-1905
1905-1923
-		-	-

За даними таблиці визначити моду і медіану.

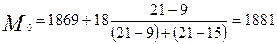тис. грн.

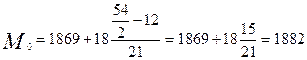тис. грн..

Відповідь: Середній товарооборот по 54 магазинах становить 1881 тис.грн.

Половина магазинів має товарооборот до 1882 тис.грн, інша половина магазинів

має товарооборот більше 1882 тис.грн.

Дата добавления: 2014-12-25