Динамические модели

Модели надежности ПО

Основным средством определения количественных показателей надежности являются модели надежности, под которыми понимают математические модели, построенные для оценки зависимости на­дежности от заранее известных или оцененных в ходе создания про­граммного средства параметров.

Известные модели надежности программного обеспечения АСОИУ делятся на 2 вида – это аналитические модели и эмпирические.

Аналитические модели реализуются в виде динамических и стати­ческих. В динамических моделях надежности программно-информа­ционных средств поведение программы (появление отказов) рассмат­ривается во времени. В статических моделях появление отказов не связывают со временем, а учитывают только зависимость количества ошибок от числа тестовых прогонов (по области ошибок) или зави­симость количества ошибок от характеристики входных данных (по области данных).

Эмпирические модели базируются на анализе структурных особен­ностей программ. Предполагает­ся, что связь между надежностью и другими параметрами является статической. Они часто не дают конкретных значений параметров надеж­ности программы. Однако их использование считается полезным на этапе проектирования программ для прогнозирования ресурсов тес­тирования и т. д.

Модель Шумана. Относится к динамическим моделям дискретного времени, данные для которой собираются в процессе тестирования программного обеспечения в течение фиксированных или случайных интервалов времени. Каждый интервал — это стадия, на которой вы­полняется последовательность тестов и фиксируется некоторое чис­ло ошибок.

Положим, что до начала тестирования имеется 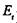ошибок. В тече­ние времени тестирования 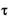обнаруживается 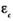ошибок в расчете на одну команду программы. Таким образом, удельное число ошибок на одну команду, оставших­ся в системе после времени тестирования, равно

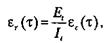
где 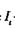— общее число команд программы.

Значение функции частоты отказов 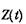пропорционально числу ошибок, оставшихся в программе после исполь­зования отведенного для тестирования времени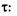

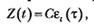
где 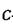- некоторая постоянная; 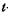- время работы программы без отказов.

Тогда вероятность безотказной работы в интервале 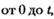будет равна

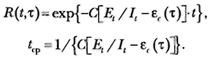
В процессе тестирования собирается инфор­мация о времени и количестве ошибок на каждом прогоне, т. е. общее время тестирования складывается из времени каждого прогона: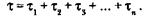

Интенсивность появления ошибок:

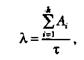
где 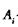— количество ошибок на 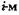прогоне.

Имея данные для двух различных моментов тестирования 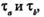можно записать следующие соотношения:

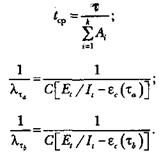
На основании приведенных выше уравнений получим

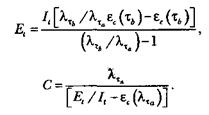
Определив значения 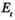и 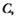можно рассчитать надежность про­граммной или информационной системы.

Модель La Padula. По этой модели выполнение последовательнос­ти тестов производится за этапов. Каждый этап заканчивается вне­сением изменений (исправлений) в тестируемую программу. Возрас­тающая функция надежности базируется на числе ошибок, обнару­женных в ходе каждого тестового прогона.

Надежность тестируемой программы в течение 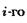этапа опреде­ляется соотношением

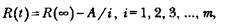где 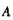— параметр роста.

Теоретически при бесконечном числе прогонов программы она будет обладать предельной надежностью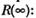

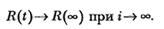
Модель является прогнозной и на основании данных тестирова­ния позволяет предсказать вероятность безотказной работы програм­мы на последующих этапах ее выполнения.

Модель Джелинского—Моранды. Исходные со­бираются в процессе тестирования программной системы. При этом фиксируется время до очередного отказа. Каждая обнаружен­ная ошибка устраняется. При этом число оставшихся ошибок умень­шается на единицу.

Функция плотности распределения времени обнаружения 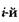ошибки, отсчитываемого от момента выявления 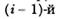ошибки, имеет вид

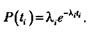
Здесь 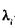— частота отказов (интенсивность отказов), которая про­порциональна числу еще не выявленных ошибок в программе:

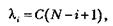
где 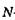- число ошибок, первоначально присутствующих в программе; 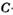— коэффициент пропорциональности. Рассчитав значение 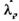можно определить вероятность безотказ­ной работы в различных временных интервалах.

Модель Шика—Волвертона. В этой модели считается, что исправление ошибок производится лишь по истече­нии интервала времени, в котором они возникли. Предполагается, что вероятность обнаружения оши­бок с течением времени возрастает. Частота ошибок (интенсивность обнаружения ошибок) 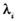предполагается постоянной в течение ин­тервала времени 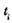и пропорциональна числу ошибок, оставшихся в программе по истечении 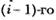интервала. Но она также пропорциональна и суммарному времени, уже затраченному на тестирова­ние (включая среднее время выполнения программы в текущем ин­тервале):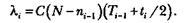

Дата добавления: 2014-12-25