Метрики сложности потока данных программ

Метрики сложности потока управления программами

С помощью этих показателей качества в процессе оценок ПО опериру­ют либо плотностью управляющих переходов внутри программ, либо взаимосвязями этих переходов. В настоящее время в мировой практике используется несколько сотен метрик программ. Рассмотрим основные.

Метрика Маккейба. Основной метрикой сложности Маккейб пред­лагает считать цикломатическую сложность графа программы, харак­теризующую трудоемкость тестирования программы.

Для вычисления цикломатического числа Маккейба C приме­няется соотношение:

C = e – n + 2

где е — число ребер; n — число узлов на графе управляющей логики. Пример:

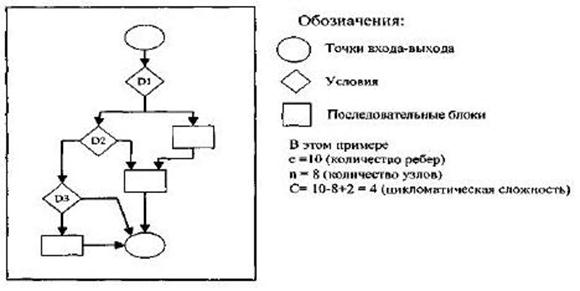
Метрика Джилба. Одной из наиболее простых, но, как считают разработчики, достаточно эффективной для оценки сложности про­грамм является метрика, предложенная Джилбом, в которой логичес­кая сложность программы определяется как насыщенность програм­мы выражениями типа IF — THEN — ELSE. При этом вводятся две ха­рактеристики:

CL — абсолютная сложность программы, характеризующаяся ко­личеством условных операторов;

cl — относительная сложность программы, характеризующаяся насыщенностью программы операторами условия, т. е. cl определя­ется как отношение CL к общему числу операторов.

Метрики сложности потоковданных определяют использование, конфигурацию и размещение данных в программах.

Метрика Чепина. Суть метода состоит в оценке информационной прочности отдельно взятого программного модуля с помощью анализа характера использования переменных из списка ввода-вывода.

Все множество переменных, составляющих список ввода-вывода, разбивается на 4 функциональные группы:

1) P – вводимые переменные для расчетов и для обеспечения вывода.

Примером может служить используемая в программах лексического анализатора переменная, содержащая строку исходного текста программы, т.е. сама переменная не модифицируется, а только содержит исходную информацию.

2) M – модифицируемые, или создаваемые внутри программы переменные.

3) C – переменные, участвующие в управлении работой программного модуля (управляющие переменные).

4) T – не используемые в программе ("паразитные") переменные.

Далее вводится значение метрики Чепина:

Q = a1*P + a2*M + a3*C + a4*T,

где a1, a2, a3, a4 – весовые коэффициенты.

Весовые коэффициенты использованы для отражения различного влияния на сложность программы каждой функциональной группы. По мнению автора метрики получается:

Q = P + 2M + 3C + 0.5T

Наряду с рассмотренными используются и другие метрики каче­ства программного обеспечения, например:

• метрики стилистики и понятности программ;

• метрика уровня комментированности программ;

• метрика изменения длины программной документации и т. д.

Дата добавления: 2014-12-25