Мощность, развиваемая источником тока во всей цепи, называется полной мощностью. 1 страница

13.

Шар

4.

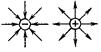
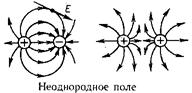
Вектор электрической индукции, в сущности, представляет собой сумму двух совершенно различных физических величин: напряженности поля и (умноженной на 4л) поляризации единицы объема среды. Тем не менее введение в рассмотрение этого вектора чрезвычайно упрощает изучение поля в диэлектриках. [3]

Итак, вектор электрической индукции представляет собой силу, действующую на точечный заряд в единицу положительного электричества, когда этот заряд помещен в бесконечно узком - зазоре, грани которого

D = e₀e E.

Поток линий

N = ES₀cos α

5. теорема Остроградского—Гаусса: поток вектора напряженности через замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на произведение электрической постоянной и диэлектрической проницаемости среды.

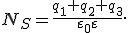
В качестве поверхности площадью S выберем цилиндрическую поверхность, образующая которой перпендикулярна плоскости. Основания этого цилиндра расположены перпендикулярно линиям напряженности по обе стороны от плоскости. Так как образующие цилиндра параллельны линиям напряженности (α = 90°, cos α = 0), то поток через боковую поверхность цилиндра отсутствует, и полный поток через поверхность цилиндра равен сумме потоков через два основания: N = 2 ES. Внутри цилиндра заключен заряд q = σS, поэтому, согласно теореме Остроградского-Гаусса, 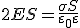, где ε = 1 (для вакуума), откуда следует, что напряженность поля равномерно заряженной бесконечной плоскости

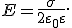
6. Поле равномерно заряженной сфериче­ской поверхности. Сферическая поверхность ра­диуса R с общим зарядом Q заряжена равно­мерно с поверхностной плотностью +0. Благодаря равномерному распределению заряда по поверхности поле, создаваемое им, обладает сферической симметрией.

Поэтому линии напря­женности направлены радиально (рис. 128). Построим мысленно сферу радиуса r, имеющую общий центр с заряженной сферой. Если r>R, то внутрь поверхности попадает весь заряд Q, создающий рассматриваемое поле, и, по теореме Гаусса (81.2), 4pr² E = Q/e ₀, откуда

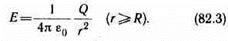
При r>R поле убывает с расстоянием r по такому же закону, как у точечного заряда. Гра­фик зависимости E от r приведен на рис. 129. Если r'<R, то замкнутая поверхность не со­держит внутри зарядов, поэтому внутри равно­мерно заряженной сферической поверхности электростатическое поле отсутствует (E =0).

радиуса R с общим зарядом Q заряжен равномерно с объемной плотностью r (r = dQ/dV — заряд, приходящийся на единицу объема). Учиты­вая соображения симметрии (см.п.3), можно показать, что для напряженности поля вне ша­ра получится тот же результат, что и в предыду­щем случае (см. (82.3)). Внутри же шара на­пряженность поля будет другая. Сфера радиуса r'<R охватывает заряд Q' =⁴/₃pr'³r. Поэтому, согласно теореме Гаусса (81.2), 4pr'² E = Q' /e₀=⁴/₃pr³r/e₀. Учитывая, что r=Q/(⁴/₃pR³), получим

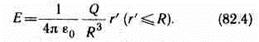
Таким образом, напряженность ноля вне равно­мерно заряженного шара описывается форму­лой (82.3), а внутри его изменяется линейно с расстоянием r' согласно выражению (82.4). График зависимости E от r приведен на рис. 130.

8. Поле равномерно заряженного бесконеч­ного цилиндра (нити). Бесконечный цилиндр

радиуса R (рис. 131) заряжен равномерно с линейной плотностью t (t=dQ/dt — заряд, приходящийся на единицу длины). Из соображений симметрии следует, что линии напряженности будут направлены по радиусам круговых сече­ний цилиндра с одинаковой густотой во все стороны относительно оси цилиндра. В качестве замкнутой поверхности мысленно построим ко­аксиальный с заряженным цилиндр радиуса r и высотой l. Поток вектора Е сквозь торцы коаксиального цилиндра равен нулю (торцы параллельны линиям напряженности), а сквозь боковую поверхность -2 prlЕ. По теореме Гаусса (81.2), при r>R 2prlE = tl /e₀, от­куда

Если r<R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области E =0. Таким образом, напряженность поля вне равномерно заряженного бесконечного цилинд­ра определяется выражением (82.5), внутри же его поле отсутствует.

9. Если в электростатическом поле точечного заряда Q из точки 1 в точку 2 вдоль про­извольной траектории (рис. 132) переме­щается другой точечный заряд Q₀, то сила, приложенная к заряду, совершает работу. Работа силы F на элементарном переме­щении dl равна

Работа при перемещении заряда Q₀ из точки 1 в точку 2

не зависит от траектории перемещения, а определяется только положениями на­чальной 1 и конечной 2 точек. Следовательно, электростатическое поле точечного заряда является потенциаль­ным, а электростатические силы — консер­вативными (см. §12).

Из формулы (83.1) следует, что рабо­та, совершаемая при перемещении элек­трического заряда во внешнем электроста­тическом поле по любому замкнутому пути L, равна нулю, т. е.

Если в качестве заряда, переносимого в электростатическом поле, взять единич­ный точечный положительный заряд, то элементарная работа сил поля на пути d l равна Е d l =E _ldl, где E_l=E cosa — про­екция вектора Е на направление элемен­тарного перемещения. Тогда формулу (83.2) можно записать в виде

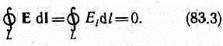
Интеграл

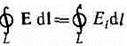
называется циркуляцией вектора напряженности. Следо­вательно, циркуляция вектора напряжен­ности электростатического поля вдоль лю­бого замкнутого контура равна нулю. Силовое поле, обладающее свойством (83.3), называется потенциальным. Из об­ращения в нуль циркуляции вектора Е следует, что линии напряженности элек­тростатического поля не могут быть за­мкнутыми, они начинаются и кончаются на зарядах (соответственно на положи­тельных или отрицательных) или же ухо­дят в бесконечность.

Формула (83.3) справедлива только для электростатического поля. В дальней­шем будет показано, что для поля движу­щихся зарядов условие (83.3) не выпол­няется (для него циркуляция вектора на­пряженности отлична от нуля).

10. Электростатический потенциа́л — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию поля, которой обладает единичный заряд, помещённый в данную точку поля.

Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:

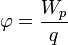
Разность потенци­алов двух точек 1 и 2 в электростатиче­ском поле определяется работой, соверша­емой силами поля, при перемещении единичного положительного заряда из точки 1 в точку 2.

Работа сил поля при перемещении за­ряда Q ₀ из точки 1 в точку 2 может быть записана также в виде

Формула электростатического потенциала (кулоновского потенциала) точечного заряда:

(где K обозначен коэффициент, зависящий от системы единиц измерения — например в СИ K = 1/(4πε₀), q — величина заряда, r — расстояние от заряда-источника до точки, для которой рассчитывается потенциал).

11. геометрическое место точек, имеющих одинаковые потенциалы, называют эквипотенциальной поверхностью

Линии Е всегда перпендикулярны по отношению к эквипотенциальной поверхности

Потенциал и напряжённость — две локальные характеристики электростатического поля. То есть, это две характеристики — энергетическая и силовая — одной и той же точки поля.

Разумно предположить, что между ними должна существовать однозначная связь.

Для отыскания этой связи, вычислим работу электрической силы на элементарном перемещении dl заряда q в электростатическом поле 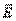(рис. 3.7.).

Рис. 3.7.

С одной стороны:

. (3.21)

Но с другой стороны, эту же работу можно связать с разностью потенциалов (j₁ – j₂) = –(j₂ – j₁) = – d j:

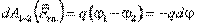. (3.22)

Объединив (3.21) и (3.22), получим:

E_ldl = – d j.

Или:

.

12. Потенциал φ∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:

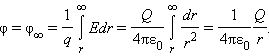
Как следует из теоремы Гаусса, эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R, где R – радиус шара.

14. Проводник – вещество, в котором в электростатическом поле возникает направленное движение свободных зарядов, т.е. электрический ток.

Поместим незаряженный проводник в однородное электростатическое поле. Под действием сил поля свободные электроны в проводнике будут перемещаться в направлении, противоположном внешнему полю, и накапливаться на поверхностях проводника, создавая электростатическое поле , направленное навстречу внешнему полю. Перемещение электронов будет происходить до тех пор, пока внешнее электростатическое поле не скомпенсируется полем, возникающим внутри проводника

В проводнике всегда есть свободные электрические заряды, имеющие возможность перемещаться по всему проводнику под действием электрического поля; в металлах – электроны, в электролитах – ионы.

Если сообщить проводнику заряд или незаряженный проводник внести в электрическое поле, то через короткий промежуток времени в проводнике установится равновесное распределение заряда, обладающее рядом свойств.

15. Способность проводника накапливать электрический заряд называют электроемкостью

Электроемкостью уединенного проводника называют отношение заряда проводника к его потенциалу:

С=q/ φ

Электроемкость численно равна заряду, который повышает потенциал проводника на единицу.

Электроемкость проводящего шара радиуса R:

С= 4π έ έ₀ R

16. Конденсатор представляет собой два проводника, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Проводники называют обкладками конденсатора и заряжают зарядами противоположного знака, равными по модулю.

Под зарядом конденсатора понимают абсолютное значение заряда одной из обкладок.

Электроемкостью конденсатора называют отношение заряда конденсатора к разности потенциалов между обкладками:

С=q/U

Электроемкость плоского конденсатора:

— Относительная диэлектрическая проницаемость

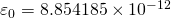- Электрическая постоянная

17. Электроемкостью конденсатора называют отношение заряда конденсатора к разности потенциалов между обкладками:

С=q/U

Электроемкость сферического конденсатора:

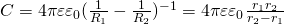
— Относительная диэлектрическая проницаемость

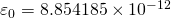- Электрическая постоянная

18. Электроемкостью конденсатора называют отношение заряда конденсатора к разности потенциалов между обкладками:

С=q/U

Электроемкость цилиндрического конденсатора:

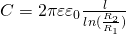
— Относительная диэлектрическая проницаемость

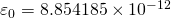- Электрическая постоянная

19. При параллельном соединении конденсаторов заряд батареи равен:

q= q₁ + q₂

Электроемкость батареи двух параллельно соединенных конденсаторов:

С = С₁ + С₂

При параллельном соединении n конденсаторов:

С = С₁ + С₂ + … + С_n

При последовательном соединении конденсаторов с электроемкостями С₁ и С₂ общий заряд батареи равен заряду каждого конденсатора: q = q₁ = q₂

Электроемкость батареи равна:

20. Энергия заряженного проводника ,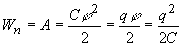

полная энергия системы заряженных проводников .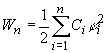

Для конденсатора

21. Энергия электрического поля

W_к = CU²/2 = ee₀S*d*E²/2 = ee₀V*E²/2

Плотность энергии — количество энергии на единицу объёма.

Плотность энергии электрического поля:

ώ = έ έ₀E²/2

22. Электрический ди­поль — система двух равных по модулю разноименных точечных зарядов (+ Q, - Q), расстояние l между которыми зна­чительно меньше расстояния до рассмат­риваемых точек поля. Вектор, направлен­ный по оси диполя (прямой, проходящей через оба заряда) от отрицательного за­ряда к положительному и равный расстоя­нию между ними, называется плечом дипо­ля l.

Вектор совпадающий по направлению с плечом диполя и равный произведению заряда

|Q| на плечо l, называется электрическим моментом диполя р или дипольным мо­ментом

Согласно принципу суперпозиции напряженность Е поля диполя в произвольной точке

Е = Е ₊ + Е _-,

где Е ₊ и Е _- — напряженности полей, со­здаваемых соответственно положительным и отрицательным зарядами. Воспользо­вавшись этой формулой, рассчитаем на­пряженность поля на продолжении оси диполя и на перпендикуляре к середине его оси.

Типы диэлектриков:

1) диэлектрики с неполярными молекулами

E₀ = 0 (в отсутствии поля)

Р_е = q l = 0

Р_е ≠ 0 (внешнее поле)

2) диэлектрики с полярными молекулами (H₂O, HCl, CH₃Cl)

Р_е ≠ 0

3) диэлектрики с ионным строением (NaCl, KCl)

23. Поляризация – изменение состояния диэлектрика, при котором он, при внесении во внешнее электрическое поле, приобретает макроскопический электрический момент.

Соответственно трем группам диэлек­триков различают три вида поляризации:

электронная, или деформационная, по­ляризация диэлектрика с неполярными молекулами, заключающаяся в возникно­вении у атомов индуцированного дипольного момента за счет деформации элек­тронных орбит;

ориентационная, или дипольная, поля­ризация диэлектрика с полярными молеку­лами, заключающаяся в ориентации име­ющихся дипольных моментов молекул по полю. Естественно, что тепловое движение препятствует полной ориентации молекул, но в результате совместного действия обо­их факторов (электрическое поле и тепло­вое движение) возникает преимуществен­ная ориентация дипольных моментов мо­лекул по полю. Эта ориентация тем сильнее, чем больше напряженность элек­трического поля и ниже температура;

ионная поляризация диэлектриков с ионными кристаллическими решетками, заключающаяся в смещении подрешетки положительных ионов вдоль поля, а отри­цательных — против поля, приводящем к возникновению дипольных моментов.

24. В диэлектрике наличие электрического поля не препятствует равновесию зарядов. Сила, действующая на заряды в диэлектрике со стороны электрического поля, уравновешивается внутримолекулярными силами, удерживающими заряды в пределах молекулы диэлектрика, так что в диэлектрике возможно равновесие зарядов, несмотря на наличие электрического поля. При достаточно большой напряженности поля и в диэлектрике возможно заметное перемещение зарядов, ведущее к пробою диэлектрика. Однако при общепринятом разделении тел на проводники и диэлектрики мы можем сказать, что в случае равновесия зарядов электрическое поле внутри проводника (например, металла) отсутствует, а электрическое поле в диэлектрике (например, в стекле) может существовать.

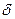- поверхностная плотность связанных зарядов

Связанные заряды. В результате процесса поляризации в объеме (или на поверхности) диэлектрика возникают нескомпенсированные заряды, которые называются поляризационными, или связанными. Частицы, обладающие этими зарядами, входят в состав молекул и под действием внешнего электрического поля смещаются из своих положений равновесия, не покидая молекулы, в состав которой они входят. Связанные заряды характеризуют поверхностной плотностью .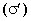

Диэлектри́ческая восприи́мчивость (или поляризу́емость) вещества — физическая величина, мера способности вещества поляризоваться под действием электрического поля. Диэлектрическая восприимчивость 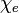— коэффициент линейной связи между поляризацией диэлектрика P и внешним электрическим полем E в достаточно малых полях:

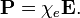
В системе СИ:

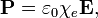
где — электрическая постоянная; произведение 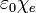называется в системе СИ абсолютной диэлектрической восприимчивостью.

В случае вакуума

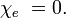
У диэлектриков, как правило, диэлектрическая восприимчивость положительна. Диэлектрическая восприимчивость является безразмерной величиной.

25. Теорема Гаусса для электростатического поля в диэлектрике:

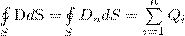(3)

т. е. поток вектора смещения электростатического поля в диэлектрике сквозь любую замкнутую поверхность равен алгебраической сумме свободных электрических зарядов, заключенных внутри этой поверхности. В такой форме теорема Гаусса верна для электростатического поля как для однородной и изотропной, так и для неоднородной и анизотропной сред.

Для вакуума D_n = ε₀E_n (ε=1), и поток вектора напряженности Е сквозь произвольно выбранную замкнутую поверхность равен

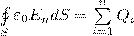
Так как источниками поля Е в среде являются как свободные, так и связанные заряды, то теорему Гаусса для поля Е в самом общем виде можно записать как

где ∑Q_i и ∑Q_sv— соответственно алгебраические суммы свободных и связанных зарядов, которые охватываются замкнутой поверхностью S. Но эта формула неприменима для описания поля Е в диэлектрике, поскольку она выражает свойства неизвестного поля Е через связанные заряды, которые, в свою очередь, определяются им же. Это еще раз показывает целесообразность введения вектора электрического смещения.

26. Электрическим током называют упорядоченное движение заряженных частиц в электрическом поле

Электрический ток называют постоянным, если движение носителей тока стационарно, т.е. скорость не меняется со временем

За направление тока принимают направление движения положительно заряженных частиц

Силой тока называют отношение заряда q, переносимого через поперечное сечение проводника площадью S за промежуток времени t, к этому промежутку:

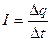
Вектором плотности тока 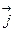называют вектор, направление которого совпадает с направлением скорости упорядоченного движения положительно заряженных частиц, а модуль равен отношению заряда 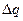, переносимого за время 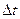через сечение 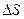, перепендикулярное к скорости дрейфа, к произведению · :

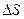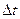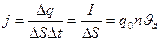
Где q₀ – заряд отдельной частицы, n – концентрация носителей

Единица плотности тока: [j]= 1A/м²

Для возникновения и поддержания постоянного тока необходимы условия:

- наличие свободных заряженных частиц

- сила, действующая на частицы в определенном направлении

27. Если между концами металлического проводника имеется разность потенциалов U, то в проводнике будет протекать электрический ток в направлении от точки a к точке b

Закон Ома для однородного участка цепи.

Сила тока в проводнике прямо пропорциональна разности потенциалов на его концах:

I=U/R

Коэффициент R называют электрическим сопротивлением проводника.

Единицей сопротивления в СИ является Ом, равный сопротивлению такого проводника, в котором при напряжении 1 В создается сила тока 1 А

1 Ом = 1В/А

Сверхпроводи́мость — свойство некоторых материалов обладать строго нулевым электрическим сопротивлением при достижении ими температуры ниже определённого значения (критическая температура).

28. При последовательном соединении проводников конец предыдущего проводника соединяется с началом последующего

Свойства последовательного соединения проводников:

- сила тока во всех последовательно соединенных проводниках одинакова:

I₁ = I₂ = … = I_n = I

- напряжение на концах рассматриваемого участка цепи равно сумме напряжений на отдельных проводниках:

U = U₁ + U₂ + … + U_n

- общее сопротивление участка цепи, состоящего из нескольких последовательно соединенных проводников:

R = R₁ + R₂ + … + R_n

- напряжения на последовательно соединенных проводниках распределяется пропорционально их сопротивлениям:

Параллельное соединение проводников подразумевает соединение концов всех проводников в два узла

При параллельном соединении проводников справедливы следующие утверждения:

- напряжения на всех проводниках и на разветвлении одинаковы:

U₁ = U₂ = … = U_n = U = φ_A - φ_B

- сила тока в неразветвленной части цепи равна сумме сил токов в ветвях

I = I₁ + I₂ + … + I_n

- величина, обратная сопротивлению участка параллельно соединенных проводников, равна:

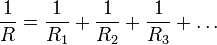
- силы тока в ветвях обратно пропорциональны сопротивлениям этих ветвей

29. Работой тока называют работу, совершаемую силами поля по переносу заряда 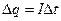на участке цепи сопротивлением R за время :

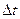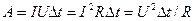
Работа тока в проводнике равна количеству выделившейся теплоты

Закон Джоуля-Ленца. Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока:

Мощностью тока Р называют отношение работы А за время 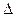t к этому интервалу времени:

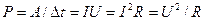
В СИ единицей измерения работы тока является Дж, а мощности ватт (Вт). На практике используют внесистемные единицы работы тока – киловатт-час (кВт ч): 1 кВт ч = 3,6 10⁶

30. R=rl/S. (98.2) I=U/R, (98.1)

Закон Ома можно представить в диф­ференциальной форме. Подставив выра­жение для сопротивления (98.2) в закон Ома (98.1), получим

I/S=(1/r)(U/l) (98.3)

где величина

обратная удельному сопротивлению, на­зывается удельной электрической прово­димостью вещества проводника. Ее едини­ца— сименс на метр (См/м). Учитывая, что U/l=E —напряженность электриче­ского поля в проводнике, I/S = j — плот­ность тока, формулу (98.3) можно запи­сать в виде

j= σE. (98.4)

Так как в изотропном проводнике носите­ли тока в каждой точке движутся в на­правлении вектора Е, то направления j и Е совпадают. Поэтому формулу (98.4) можно записать в виде

Дата добавления: 2014-12-25