Мощность, развиваемая источником тока во всей цепи, называется полной мощностью. 2 страница

j = σ E. (98.5)

Выражение (98.5) — закон Ома в диффе­ренциальной форме, связывающий плот­ность тока в любой точке внутри провод­ника с напряженностью электрического поля в этой же точке. Это соотношение справедливо и для переменных полей.

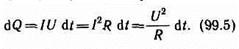
Выражение (99.5) представляет собой за­кон Джоуля — Ленца, экспериментально установленный независимо друг от друга Дж. Джоулем и Э. X. Ленцем.

Выделим в проводнике элементарный цилиндрический объем dV=dSd l (ось ци­линдра совпадает с направлением тока),

сопротивление которого R= r(d l /dS). По закону Джоуля — Ленца, за время d t в этом объеме выделится теплота

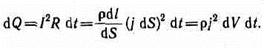
Количество теплоты, выделяющееся за единицу времени в единице объема, на­зывается удельной тепловой мощностью

тока. Она равна

w=rj². (99.6)

Используя дифференциальную форму за­кона Ома (j =gE) и соотношение r=1/ σ, получим

w = jE = σ E ². (99.7)

Формулы (99.6) и (99.7) являются обоб­щенным выражением закона Джоуля — Ленца в дифференциальной форме, при­годным для любого проводника.

31. Сторонние силы – силы неэлектростатического происхождения, действующие в источнике тока. Электрическое поле в проводниках поддерживается благодаря работе сторонних сил.

Участки цепи, где заряды движутся под действием кулоновских сил, называют однородными, а участки, где присутствуют сторонние силы, - неоднородными.

Электродвижущая сила источника тока (ЭДС) равна отношению работы сторонних сил А_ст по перемещению заряда q вдоль контура к этому заряду:

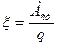
Она определяется по формуле

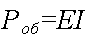
где P_об-полная мощность, развиваемая источником тока во всей цепи, вт;

Е- э. д. с. источника, в;

I-величина тока в цепи, а.

Заменяя в выражении полной мощности величину э. д. с. через напряжения на участках цепи, получим

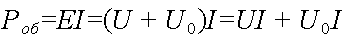
Величина UI соответствует мощности, развиваемой на внешнем участке цепи (нагрузке), и называется полезной мощностью P_пол=UI.

Величина U_oI соответствует мощности, бесполезно расходуемой внутри источника, Ее называют мощностью потерь P_o=U_oI.

Таким образом, полная мощность равна сумме полезной мощности и мощности потерь P_об=P_пол+P_0.

Отношение полезной мощности к полной мощности, развиваемой источником, называется коэффициентом полезного действия, сокращенно к. п. д.,и обозначается η.

Из определения следует

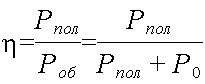
При любых условиях коэффициент полезного действия η ≤ 1.

Если выразить мощности через величину тока и сопротивления участков цепи, получим

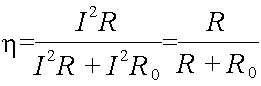
Таким образом, к. п. д. зависит от соотношения между внутренним сопротивлением источника и сопротивлением потребителя.

Обычно электрический к. п. д. принято выражать в процентах.

34. На неоднородном участке цепи действуют как электрические, так и сторонние силы.

Напряжение на участке цепи равно отношению алгебраической суммы работ электростатических и сторонних сил по переносу заряда q на данном участке к переносимому заряду:

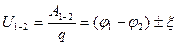
Полное сопротивление участка:

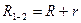
Закон Ома для неоднородного участка цепи:

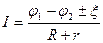
Правило знаков: перед I берут знак «+», если направление тока совпадает с направлением от 1 к 2, и наоборот.

Все электрические цепи, по которым протекает постоянный электрический ток, должны быть замкнутыми

Закон Ома для полной(замкнутой) цепи:

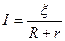
Напряжение на зажимах источника равно напряжению на резисторе R:

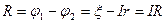
35. Первый закон Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю:

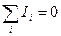
Второй закон Кирхгофа:

В любом замкнутом контуре, произвольно выбранном в разветвленной цепи постоянного тока, сумма падений напряжения в ветвях контура равна алгебраической сумме ЭДС в этом контуре:

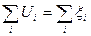
Где 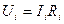- падение напряжения на резисторе, 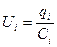- падение напряжения на конденсаторе

36. Последовательное соединение источников – это соединение, при котором один полюс промежуточного источника соединяется с полюсом произвольного знака предыдущего, а второй полюс промежуточного источника соединяется с полюсом последующего источника.

ЭДС батареи равна разности потенциалов на ее зажимах:

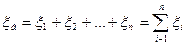
В зависимости от полярности ЭДС 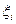войдет в сумму с тем или иным знаком.

Если такую батарею замкнуть на резистор, то в цепи будет сила тока:

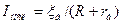
Где R – внешнее сопротивление, а сопротивление батареи - 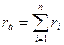- арифметическая сумма.

Параллельное соединение источников – такое, при котором одни полюса соединяют в один узел, другие в другой. При таком соединении внутри даже отключенной от нагрузки батареи могут протекать точки, и разность потенциалов на ее полюсах рассчитывается по правилам Кирхгофа.

37. Носителями тока в метал­лах служат свободные электроны. Это подтверждалось рядом классических опытов.

В опыте К.Рикке (1901 г.)электрический ток в течение года пропускался че­рез три последовательно соединенных металлических цилиндра (Cu, A l, Cu) с от­шлифованными торцами одинакового радиуса. Общий заряд, прошедший через ци­линдры, равнялся 3.5×10⁶ Кл. Проведенное после этого взвешивание показало, что вес цилиндров не изменился, также не было обнаружено проникновения одного металла в другой. Следовательно, перенос заряда осуществлялся не ионами, а общими для всех металлов частицами - электронами.

Для подтверждения этого положения необходимо было определить знак и ве­личину удельного заряда q/m (заряда единицы массы)носителей тока. Идея опытов и их качественное воплощение принадлежит российскими физиками Л.Мандельштаму и Н.Папалески (1913 г.). Если движущийся поступательно проводник резко остановить, то, подклю­ченный к нему гальванометр зафиксирует кратковременный ток. Это объясняется тем, что носители тока не связаны жестко с кристаллической решеткой и при тор­можении продолжают двигаться по инерции. По направлению тока гальванометра было определено, что знак заряда носителя тока -отрицательный. Согласно численному расчету, удельный заряд носителя тока оказался приблизительно равным удельному заряду электрона. К таким же результатам привели опыты Ч.Стюарта и Т.Толмена (1916 г.), в которых быстрые крутильные колебания катушки, соединенной с чувстви­тельным гальванометром, создавали переменный электрический ток. Таким образом, было доказано, что носителями электрического тока в метал­лах являются свободные электроны.

38. Основные положения КЭТ.

1) металлический проводник рассматривается как совокупность ионов находящихся в узлах кристаллической решетки и свободных электронов, т.е. бывших валентных атомов потерявших с ними связь и превративших их в полярные ионы

2) свободные электроны находятся в состоянии беспрерывного хаотичного движения, подобно молекулам идеального газа

3) свободные электроны рассматривают как некий газ, подобный идеальному газу молекулярной физики

39. Пусть в металлическом проводнике существует электрическое по­ле напряженностью Е= const. Co стороны поля заряд е испытывает действие силы F=eE и приобретает ускорение а=F/m=еЕ/т. Таким образом, во время сво­бодного пробега электроны движутся рав­ноускоренно, приобретая к концу свобод­ного пробега скорость

v_max= еE<t>.

где < t >—среднее время между двумя последовательными соударениями элек­трона с ионами решетки.

Согласно теории Друде, в конце сво­бодного пробега электрон, сталкиваясь с ионами решетки, отдает им накопленную в поле энергию, поэтому скорость его упо­рядоченного движения становится равной нулю. Следовательно, средняя скорость направленного движения электрона

<v>=(v_max+0)/2= eE<t>/(2m). (103.1)

Классическая теория металлов не учи­тывает распределения электронов по ско­ростям, поэтому среднее время < t > сво­бодного пробега определяется средней длиной свободного пробега < l > и средней скоростью движения электронов относи­тельно кристаллической решетки провод­ника, равной <u>+(v) (< u > — средняя скорость теплового движения электронов). В §102 было показано, что (v)<< <u>, поэтому

<t>=< l >/<u>.

Подставив значение < t >в формулу (103.1), получим

<v>=eE< l >/(2m<u>).

Плотность тока в металлическом провод­нике, по (96.1),

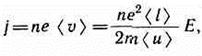
откуда видно, что плотность тока пропор­циональна напряженности поля,

т. е. получили закон Ома в дифференци­альной форме (ср. с (98.4)). Коэффициент пропорциональности между j и Е есть не что иное, как удельная проводимость ма­териала

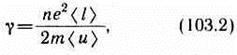
которая тем больше, чем больше концен­трация свободных электронов и средняя длина их свободного пробега.

Закон Джоуля-Ленца

Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину электрического поля

Математически может быть выражен в следующей форме:

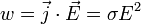
где 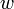— мощность выделения тепла в единице объёма, 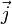— плотность электрического тока, 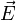— напряжённость электрического поля, σ — проводимость среды.

Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка

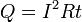
40. Метал­лы обладают как большой электропровод­ностью, так и высокой теплопроводностью. Это объясняется тем, что носителями тока и теплоты в металлах являются одни и те же частицы — свободные электроны, кото­рые, перемещаясь в металле, переносят не только электрический заряд, но и прису­щую им энергию хаотического теплового движения, т. е. осуществляют перенос теплоты.

Видеманом и Францем в 1853 г. экспе­риментально установлен закон, согласно которому отношение теплопроводности (l) к удельной проводимости (g) для всех металлов при одной и той же температуре одинаково и увеличивается пропорцио­нально термодинамической температуре:

χ/g=аT,

где а — постоянная, не зависящая от рода металла.

Элементарная классическая теория электропроводности металлов позволила найти значение а: а=3(k/e)², где k — пос­тоянная Больцмана.

Успехи:

1. Объяснение электрического сопротивления R
2. Объяснение законов Ома и Джоуля Ленца
3. Качественное объяснение закона Видемана Франца

41. Работой выхода A_вых называется минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл. Свободные электроны, выходя за пределы кристаллической решетки металла, образуют вокруг него электронное облако. Между ним и кристаллической решеткой создается электрическое поле, препятствующее дальнейшему выходу электронов из металла. Для того, чтобы электрон покинул металл, он должен обладать достаточной энергией для преодоления этого поля. Скорости электронов в системе различны. Электрону с меньшей энергией надо сообщить большую порцию энергии, чем электрону с меньшей энергией, для того чтобы они покинули металл. Работа выхода A_вых зависит только то химического состава металла и от состояния его поверхности.

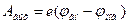
Контактная разность потенциалов — это разность потенциалов, возникающая при соприкосновении двух различных проводников, находящихся при одинаковой температуре.При соприкосновении двух проводников с разными работами выхода на проводниках появляются электрические заряды. А между их свободными концами возникает разность потенциалов. Разность потенциалов между точками находящимися вне проводников, в близи их поверхности называется контактной разностью потенциалов^[1].

Законы Вольты:

1. на контакте двух разных металлов возникает разность потенциалов, которая зависит от химической природы и от температуры спаев
2. разность потенциалов на концах последовательно соединенных проводников не зависит от промежуточных проводников и равна разности потенциалов, возникающей при соединении крайних проводников при той же температуре

43. Согласно второму закону Вольта, в за­мкнутой цепи, состоящей из нескольких металлов, находящихся при одинаковой температуре, э.д.с. не возникает, т. е. не происходит возбуждения электрического тока. Однако если температура контактов не одинакова, то в цепи возникает элек­трический ток, называемый термоэлектри­ческим. Явление возбуждения термоэлек­трического тока (явление Зеебека), а так­же тесно связанные с ним явления Пельтье и Томсона называются термо­электрическими явлениями.

Эффект Зеебека состоит в том, что в замкнутой цепи, состоящей из разнородных проводников, возникает термо-ЭДС, если места контактов поддерживают при разных температурах. Цепь, которая состоит только из двух различных проводников называется термоэлементом или термопарой.

Величина возникающей термоэдс зависит только от материала проводников и температур горячего (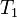) и холодного (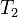) контактов.

В небольшом интервале температур термоэдс 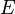можно считать пропорциональной разности температур:

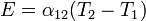, где 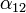— термоэлектрическая способность пары (или коэффициент термоэдс).

В простейшем случае коэффициент термоэдс определяется только материалами проводников, однако строго говоря, он зависит и от температуры, и в некоторых случаях с изменением температуры 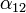меняет знак.

Эффект Пельтье — термоэлектрическое явление, при котором происходит выделение или поглощение тепла при прохождении электрического тока в месте контакта (спая) двух разнородных проводников. Величина выделяемого тепла и его знак зависят от вида контактирующих веществ, направления и силы протекающего электрического тока:

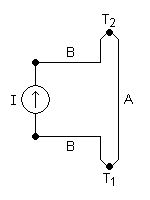
Q = П_АBIt = (П_B-П_A)It, где

Q — количество выделенного или поглощённого тепла;

I — сила тока;

t — время протекания тока;

П — коэффициент Пельтье, который связан с коэффициентом термо-ЭДС α вторым соотношением Томсона ^[1] П = αT, где Т — абсолютная температура в K.

44. Итак, по двум длинным прямым параллельным проводникам, находящимся на расстоянии R друг от друга (которое во много, раз в 15 меньше длин проводников), протекают постоянные токи I ₁, I ₂.

В соответствии с полевой теорией взаимодействие проводников объясняется следующим образом: электрический ток в первом проводнике создает магнитное поле, которое взаимодействует с электрическим током во втором проводнике. Чтобы объяснить возникновение силы, действующей на первый проводник, необходимо проводники «поменять ролями»: второй создает поле, которое действует на первый. Повращайте мысленно правый винт, покрутите левой рукой (или воспользуйтесь векторным произведением) и убедитесь, что при токах текущих в одном направлении, проводники притягиваются, а при токах, текущих в противоположных направлениях, проводники отталкиваются ^[1].

Таким образом, сила, действующая на участок длиной Δ l второго проводника, есть сила Ампера, она равна

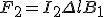, (1)

где B ₁ - индукции магнитного поля, создаваемого первым проводником. При записи этой формулы учтено, что вектор индукции 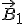перпендикулярен второму проводнику.

Силой Ампера называют силу, действующую на проводник длиной l, по которому течет ток I в магнитном поле с индукцией :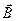

,

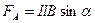Где - угол между направлением вектора магнитной индукции 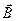и направлением тока

Дата добавления: 2014-12-25