Модели линейного программирования

Задачи математического и линейного программирования.

Нередко экономические задачи имеют не единственное решение и требуется выбрать лучшее – оптимальное из них. Моделирование таких задач сводится к задачам математического программирования (ЗМП).

Математическое программирование – область математики, изучающая оптимизационные процессы посредством поиска экстремума функции при заданных ограничениях.

Сформулируем в общем виде ЗМП:

(7)

при условиях

(8)

(9)

где – целевая функция, условия (8) – специальные ограничения, условия (9) – общие ограничения ЗМП.

Точку , координаты которой удовлетворяют ограничениям (8) и (9), называют допустимым решением ЗМП.

Множество всех допустимых решений ЗМП называют допустимым множеством.

Допустимое решение , удовлетворяющее соотношению (7), называют оптимальным решением ЗМП.

Если в ЗМП целевая функция и функции , – линейные, то имеем общую задачу линейного программирования (ЗЛП):

(10)

(11)

(12)

В зависимости от вида специальных ограничений различают следующие ЗЛП:

- каноническая ЗЛП, включающая в качестве ограничений (11) только уравнения, т. е.

;

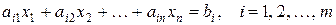- стандартная ЗЛП, включающая в качестве ограничений (11) только неравенства, т. е.

Рассмотрим следующие примеры моделей, приводимых к ЗЛП.

Пример 1. Экономико-математическая модель задачи о планировании производства.

На заводе имеются запасы трех видов сырья: 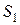, 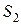и 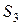, из которого можно наладить производство двух видов товаров: 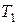и 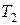. Запасы сырья, норма его расхода на производство единицы товаров, а также прибыль от реализации единицы каждого товара приведены в таблице 1 (цифры условные).

Таблица 1

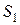
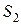
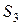
Сырье Товары				Прибыль
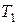
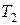
Запасы

Необходимо составить такой план производства товаров, при котором прибыль от их реализации будет максимальной.

Решение.

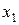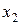План производства зададим числами и , где 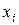– количество единиц товара , которое следует произвести . Неизвестные 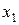и 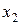должны удовлетворять условиям

или , (13)

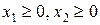(14)

Поясним смысл первого неравенства системы (13). В левой части записано количество сырья 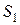, которое расходуется на выпуск 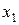единиц товара 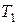и 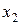единиц товара 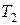. Это количество не должно превышать имеющегося запаса сырья 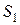, т. е. 126 единиц. Аналогичный смысл имеют второе и третье неравенства системы (13).

Прибыль, предприятия от реализации плана (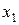, 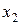) производства товаров, очевидно, составит

. (15)

В интересах предприятия максимизировать эту прибыль. Следовательно, чтобы составить план производства товаров, при котором прибыль от их реализации будет максимальной нужно решить стандартную ЗЛП: при условиях (13) и (14):

Пример 2. Экономико-математическая модель задачи о диете.

Имеются два вида продуктов: и 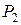. Содержание в 1 кг питательных веществ A, B и C, ежесуточные потребности организма V в них и стоимость S 1 кг продуктов приведены в таблице 2

Таблица 2

Витамины Продукты	A	B	C	S
V

Составить такую ежесуточную диету, которая обеспечивает необходимое количество питательных веществ при минимальных затратах на продукты.

Решение.

Пусть 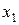и 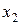– искомые количества продуктов и 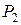соответственно. Их стоимость составляет

Общее количество питательного вещества A в обоих видах продуктов равно . Оно должно быть не меньше 6 единиц: .

Аналогичные неравенства составим для питательных веществ B и C: и .

Очевидно, и .

Таким образом, получим следующую стандартную ЗЛП:

(16)

при условиях

(17)

Дата добавления: 2014-12-25