Симплекс-метод для решения задач линейного программирования. 2 страница

В строке (F) нет отрицательных чисел. Получили оптимальное решение:

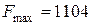
при , , , .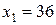

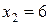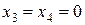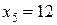Замечание. Симплекс-таблицы удобнее «пристыковывать» друг к другу по вертикали, что позволяет не писать многократно заглавную строку

II. Вторая основная задача.

Для заполнения первой симплекс-таблицы перепишем целевую функцию F и систему ограничений (6.14), имеющую допустимый вид, следующим образом:

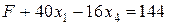
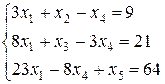
Заполним таблицу

Базисные неизвестные	Свободные члены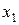
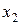
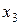
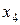
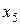
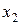
					–1
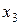
					–3
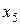
					–8
F					–16
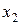
	1,125			–0,375	0,125
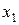
	2,625			0,125	–0,375
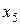
	3,625			–2,875	0,625
F				–5	–1

В выражении для F выясняем, имеются ли в последней строке таблицы, кроме столбца «свободные члены», положительные числа. Если таковых нет, то задача решена. Если же есть, то выполняем преобразование: в столбце 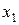имеем 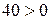. Над этим элементом ищем положительные числа. Если таковых нет, то задача не имеет решения. В нашем случае над 40 есть три положительных числа: 3; 8 и 23.

Найдем

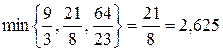
Элемент, стоящий на пересечении строки (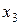) и столбца (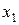) разрешающий и равен 8. Неизвестная 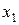вводится в базис, а неизвестная 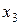выводится из него. Все элементы строки (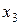) разделим на разрешающий элемент. Полученные результаты запишем в новую симплекс-таблицу в строке ().

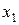Преобразуем строки (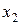), () 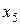и (F) первой таблицы так, чтобы их элементы, стоящие в столбце (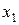), обратились в 0. С этой целью

1) умножим элементы строки (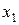) на 3, вычтем из соответствующих элементов строки (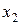), и запишем полученные результаты в строку (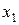) второй таблицы;

2) умножим элементы строки (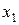) на 23, вычтем из соответствующих элементов строки (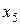), и запишем полученные результаты в строку (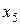) второй таблицы;

3) умножим элементы строки (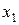) на 40, вычтем из соответствующих элементов строки (F), и запишем полученные результаты в строку (F) второй таблицы.

В строке (F) нет положительных чисел. Получили оптимальное решение: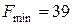

при , , , .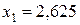

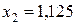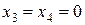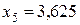Замечание. Первая симплекс-таблица второй основной задачи была заполнена с учетом того, что система ограничений (6.11) была предварительно сведена к допустимому виду (6.14), т.е. был найден допустимый базис. Зачастую поиск такого базиса довольно затруднителен. Рассмотрим следующий метод нахождения допустимого базиса, который называют методом искусственного базиса или М-методом.

Метод искусственного базиса (М-метод).

Применительно к рассматриваемой задаче М-метод заключается в следующем. В каждое уравнение системы ограничений (6.11), введем свою новую искусственную неизвестную: 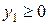, 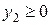и 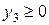. Включим их в число базисных неизвестных и составим новую функцию цели

,

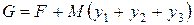где М – произвольно большое положительное число.

В результате получили следующую ЗЛП, приведенную к допустимому виду

.

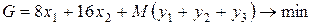
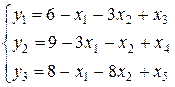
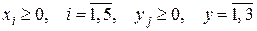Эту задачу называют М-задачей.

Сформулируем утверждения, устанавливающие связь между решениями исходной задачи и М-задачи.

1. Если в оптимальном решении М-задачи все искусственные переменные равны 0, то соответствующие значения остальных переменных дают оптимальное решение исходной задачи (т.е. 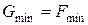, если ).

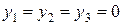2. Если имеется оптимальное решение М-задачи, в котором хотя бы одна из искусственных переменных отлична от 0, то исходная задача не имеет допустимого решения.

3. Если М-задача не имеет оптимального решения, то исходная задача неразрешима (т.е. если 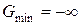, то либо 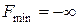, либо нет ни одного допустимого решения).

Из этих утверждений следует следующее правило решения M-задачи симплекс-методом:

а) Необходимо выбирать последовательность шагов таким образом, чтобы все искусственные неизвестные 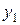, , 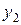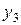вышли из базиса, т.е. стали свободными.

б) В симплекс-таблице отбросив столбцы для этих неизвестных, получим симплекс-таблицу, дающую оптимальное решение исходной задачи.

в) Если при решении М-задачи получена симплекс-таблица, дающее оптимальное решение, и в этой таблице хотя бы одна искусственная переменная 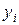входит в базис, причем в строке для 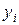свободный член положителен, то исходная задача не имеет ни одного допустимого решения.

Составим симплекс-таблицы решаемой задачи.

Базисные неизвест ные	Свободные члены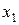
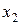
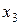
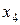
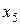
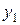
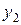
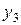
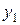
				–1
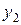
					–1
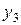
						–1
G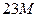
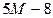
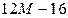
				–1
					–1
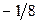
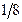
G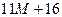
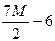
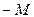
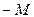
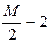
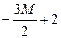
				–1
G
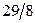
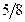
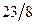
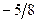
									–1
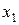
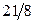
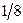
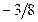
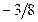
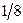
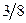
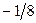
G				–5	–1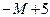

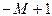
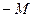
ЛЕКЦИЯ 6

Дата добавления: 2014-12-25