Решение матричных игр в смешанных стратегиях

Рассмотрим конечные матричные игры, в которых нет седловой точки, т.е. .

Нетрудно доказать, что . Если игра одноходовая, то по принципу минимакса игроку А гарантирован выйгрыш , а игроку В – проигрыш 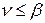. Таким образом, для цены игры справедливо соотношение

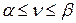(48)

Если игра повторяется неоднократно, то постоянный выбор игроками минимаксных стратегий не логичен. Действительно, игрок В, зная что игрок А применяет лишь минимаксную стратегию , выберет иную стратегию – стратегию, соответствующую наименьшему элементу в строке платежной матрицы. Такие же рассуждения имеют место и для поведения игрока А. Следовательно, при неоднократном повторении игры игрокам необходимо менять стратегии. Выясним механизм выбора игроками оптимальных стратегий, а также что принять за стоимость игры.

Рассмотрим матричную игру, заданную таблицей 6.

Таблица 6

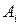
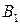
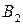
		¼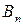
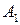
			¼
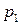
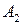
			¼
¼	¼	¼	¼	¼	¼
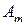
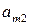
			¼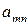
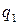
			¼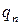

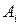Через и обозначим соответственно вероятности (относительные частоты), согласно которым игроки А и В выбирают стратегии и .

Очевидно, что , , , 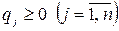. Упорядоченные множества 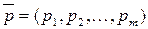и полностью определяет характер игры игроков А и В и называются их смешанными стратегиями. Отметим, что любая их чистая стратегия 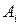и может быть описана как смешанная. Действительно, или .

Пусть игроки А и В применяют смешанные стратегии p и q, выбирают их случайно. Тогда вероятность выбора комбинации будет равна .

Игра приобрела случайный характер. Следовательно, случайной становится и величина выигрыша.

Этой величиной является математическое ожидание выигрыша, которое определяется формулой:

Функцию называют платежной функцией игры с заданной матрицей. Как и выше, введем понятие нижней и верхней цены игры, сохраняя при этом обозначения 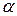и :

, .

Оптимальными смешанными стратегиям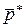и и 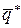называют такие стратегии, при которых . Величину 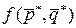называют ценой игры v.

Для практических целей важны следующие свойства оптимальных смешанных стратегий, выражаемые следующими теоремами.

Сформулируем основную теорему теории игр.

Теорема (Нейман): Любая конечная матричная игра имеет, по крайней мере, одно оптимальное решение, возможно, среди смешанных стратегий.

Теорема 1. Для того чтобы смешанные стратеги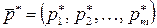и и 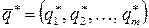были оптимальными, необходимо и достаточно выполнение неравенств

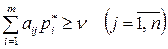(49)

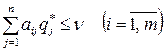(50)

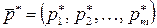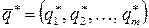Теорема 2. Пусть и – оптимальные смешанные стратегии и – цена игры.

Только те вероятности 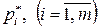, отличны от нуля, для которых

.

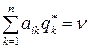Только те вероятности 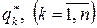, отличны от нуля, для которых

.

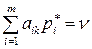Методы решения матричных игр в смешанных стратегиях.

В этой лекции рассматриваются матричные игры, не имеющие седловых точек.

Дата добавления: 2014-12-25