Решение матричных игр в чистых стратегиях

Предмет теории игр. Основные понятия.

В условиях рыночной экономики возникают ситуации, в которых сталкиваются интересы двух и более сторон. Такие ситуации относятся к конфликтным. Например, взаимоотношения между поставщиком и потребителем, покупателем и продавцом, банком и клиентом. Для конфликтных ситуаций оптимальность решений, принимаемых каждой из сторон, существенно зависит от действий другой стороны. При этом ни одна из сторон не может полностью контролировать положение, т.к. обеим сторонам приходится принимать решение в условиях неопределенности. Раздел математики, изучающий конфликтные ситуации на основе их математических моделей, называется теорией игр.

Отметим основные ее понятия:

игра – упрощенная математическая модель конфликтной ситуации, отличающаяся от реальной темы, что ведется по определенным правилам, при этом каждый из участников принимает такие решения, которые, как он полагает, обеспечат ему наилучший исход;

исход игры – значение некоторой функции, называемой функцией выигрыша ли платежной функцией, которая может задаваться либо аналитическим выражением, либо матрицей;

стратегия – совокупность правил, однозначно определяющих последовательность действий игрока в каждой конкретной ситуации. Величина выигрыша зависит от стратегии игрока. Всякая игра состоит из партий;

партией называют каждый вариант реализации игры. В партии игроки совершают конкретные ходы;

ход – выбор и реализация игроком одного из допустимых вариантов поведения.

Целью теории игр является определение оптимальной стратегии для каждого игрока.

Игры можно классифицировать по разным признакам:

Например:

- по количеству стратегий игры делятся на конечные и бесконечные;

- по взаимоотношению участников на бескоалиционные (без права заключения соглашения), некооперативные, и коалиционные (кооперативные);

- по характеру выигрышей на игры с нулевой суммой (общий капитал игроков не меняется, а лишь перераспределяется в ходе игры, при этом сумма выигрышей равна 0, а проигрыш есть отрицательный выигрыш и с ненулевой суммой;

- по виду платежной функции на матричные и непрерывные;

- по количеству ходов игры на одноходовые и многоходовые (многоходовые игры подразделяются на стохастические и дифференциальные уравнения).

Ограничимся изучением парных матричных игр с нулевой суммой, а именно таких игр, в которых у каждого из двух игроков А и В конечное число возможных ходов – чистых стратегий.

Пусть у игроков А и В соответственно m и n чистых стратегий, которые обозначим через и .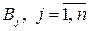

Выбор игроками любой пары стратеги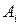й и однозначно определяет исход игры, описываемый числом . Матрица называется платежной матрицей, где – выигрыш игрока А и проигрышь 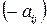игрока В.

Платежную матрицу удобно также представить в виде таблицы 5

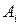
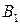
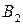
			¼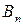
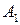
			¼
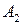
			¼
¼	¼	¼	¼	¼
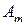
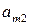
			¼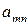

В ее строках расположены чистые стратегии игрока А, а в столбцах – чистые стратегии игрока В.

Цель матричной игры – выбор наиболее выгодных стратегий, доставляющих игроку А максимальный выигрыш, а игроку В – минимальный проигрыш. Стратегию игрока А называют оптимальной, если при ее применении выигрыш игрока А не уменьшается при любой стратегии игрока В. Оптимальной для игрока В называют стратегию, при которой проигрыш игрока В не увеличивается при любой стратегии игрока А. При поиске оптимальных стратегий игроки соблюдают принцип осторожности, согласно которому противник является по меньшей мере таким же разумным и не упустит ни единой возможности использовать любую ошибку соперника в своих интересах. Пусть игрок А выбрал некоторую стартегию 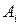. Сначала он найдет минимальное значение ожидаемого выигрыша: , а затем из всех выберет наибольшее .

Число a называют нижней ценой игры и является гарантированным выигрышем игрока А.

Очевидно, a находится в одной из строк матрицы H, к примеру в строке . Тогда стратегию называют максиминной, т.к. .

В свою очередь игрок В, стремясь минимизировать проигрыш и используя принцип осторожности, сначала для каждой чистой стратегии найдет максимально возможный проигрыш – 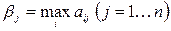, а затем среди 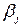выберт минимальное значение . Ему будет соответствовать чистая стратегия , называемая минимаксной, т.к. . Число называют верхней ценой игры. Оно показывает какой максимальный проигрыш может быть у игрока В. Таким образом, правильно используя чистые стратегии, игрок А обеспечит выигрыш не меньше a, а игрок В не позволит игроку А выиграть больше чем b.

Рассмотрим примеры нахождения 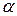и .

Пример 1. Пусть игра задана платежной матрицей :

Выпишем для каждой строки справа от матрицы , а снизу каждого столбца. Тогда получим

Верхняя и нижняя цены игры совпали: .

Пример 2. Задана платежная матрица

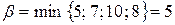
Здесь .

Теорема 1. В любой матричной игре нижняя цена игры не превосходит верхней цены игры, т.е. .

Обозначим через и номера чистых стратегий, при котором 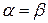. Пару чистых стратегий и 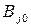при этом называют седловой точкой игры, а – седловым элементом платежной матрицы.

Число 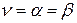называют чистой ценой игры. Простота решения игры с седловой точкой заключается в том, что сразу найдены оптимальные стратегии: максиминная для игрока А и минимаксная для игрока В, а цена игры – седловой элемент платежной матрицы: . Отметим, что матричная игра может содержать несколько седловых точек. Максиминные и минимаксные стратегии называют общим термином – минимаксными стратегиями, а их выбор – принципом минимакса.

Дата добавления: 2014-12-25