
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
И – игры
|
|
|
|
Игры.
Рассмотрим игру с платежной матрицей

Пусть игрок A применяет набор своих оптимальных стратегий  . По основной теореме теории игр это обеспечивает ему выигрыш
. По основной теореме теории игр это обеспечивает ему выигрыш  при любых стратегиях игрока В, т.е. выполняются соотношения:
при любых стратегиях игрока В, т.е. выполняются соотношения:
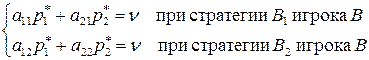 (51)
(51)
Дополняя их уравнением
 (52)
(52)
получим систему линейных уравнений относительно 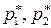 и
и  . Решая ее найдем
. Решая ее найдем
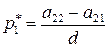 ,
, 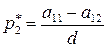 ,
,  , (53)
, (53)
где 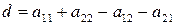 .
.
Повторяя те же рассуждения для игрока В, получим систему линейных уравнений
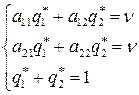 (54)
(54)
Ее решениями будут
 ,
, 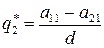 ,
,  , (55)
, (55)
Пример. Молокозавод поставляет в магазин молочную продукцию ( ) и кисломолочную продукцию (
) и кисломолочную продукцию ( ). Согласно договора между ними продукция поступает в магазин два раза в день: с 10.00 до 11.00 (1-ый срок) и с 17.00 до 18.00 (2-ой срок). Если молокозавод соблюдает сроки поставок, то магазин выплачивает премии по следующей схеме: при поставке продукции
). Согласно договора между ними продукция поступает в магазин два раза в день: с 10.00 до 11.00 (1-ый срок) и с 17.00 до 18.00 (2-ой срок). Если молокозавод соблюдает сроки поставок, то магазин выплачивает премии по следующей схеме: при поставке продукции  в первый срок выплачивает 5 тыс. руб., во второй срок – 3 тыс. руб.; при поставке продукции
в первый срок выплачивает 5 тыс. руб., во второй срок – 3 тыс. руб.; при поставке продукции  в первый срок выплачивает 2 тыс. руб., во второй срок – 3 тыс. руб. Определить оптимальные стратегии поставок и получения продукции.
в первый срок выплачивает 2 тыс. руб., во второй срок – 3 тыс. руб. Определить оптимальные стратегии поставок и получения продукции.
Решение. Примем молокозавод за игрока А, а магазин – за игрока В. Составим платежную матрицу игры:
| Сроки Продукция | 1-ый срок | 2-ой срок |

| ||

|
или

Найдем

 ,
,
 , седловой точки нет. Применим формулы (53) – (55) для определения оптимальных стратегий и цены игры:
, седловой точки нет. Применим формулы (53) – (55) для определения оптимальных стратегий и цены игры:
 ,
,  ,
, 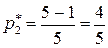 ,
,  ,
,
 ,
,  ,
,
Оптимальные стратегии: 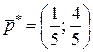 ,
,  , цена игры
, цена игры 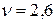 .
.
Таким образом, молокозавод поставляет молочную продукцию с вероятностью  , а кисломолочную продукцию – с вероятностью
, а кисломолочную продукцию – с вероятностью  , а магазин получает продукцию в 1-ый срок с вероятностью
, а магазин получает продукцию в 1-ый срок с вероятностью  , а во 2-ой срок – с вероятностью
, а во 2-ой срок – с вероятностью 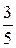 и выплачивает 2,6 тыс. руб. премии молокозаводу ежедневно.
и выплачивает 2,6 тыс. руб. премии молокозаводу ежедневно.
Матричная игра 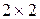 допускает простую геометрическую интерпретацию.
допускает простую геометрическую интерпретацию.
Нахождение цены игры  и оптимальной стратегии
и оптимальной стратегии 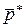 для игрока А равносильно решению уравнения:
для игрока А равносильно решению уравнения:
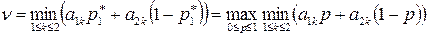 (56)
(56)
Для нахождения правой части (56) применим графический метод.
Пусть игрок А выбрал смешанную стратегию  ,
,  , а игрок В – k -ую чистую стратегию,
, а игрок В – k -ую чистую стратегию,  . Тогда средний выигрыш игрока А окажется равным
. Тогда средний выигрыш игрока А окажется равным
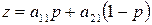 при стратегии
при стратегии 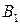 (57)
(57)
 при стратегии
при стратегии 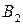 (58)
(58)
Очевидно,  , которую называют нижней огибающей прямых I и II.
, которую называют нижней огибающей прямых I и II.
Нетрудно видеть, что 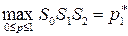
Таким образом, верхняя точка нижней огибающей – 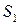 определяет оптимальную стратегию игрока А:
определяет оптимальную стратегию игрока А:  и цену игры
и цену игры  .
.
Проиллюстрируем описанный графичексий метод на рассмотренной выше игре с платежной матрицей  .
.
На плоскости pOz построим две прямые, описываемые уравнениями:  и
и 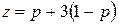 или
или  (I) и
(I) и  (II).
(II).
Решая систему уравнений

найдем  ,
,  ,
,  .
.
Таким образом, имеем полученный выше ответ игры: 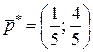 и
и 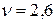 .
.
Теперь покажем как графическим методом найти стратегии игрока В.
 (59)
(59)
Пусть игрок В выбрал смешанную стратегию  ,
,  , а игрок А – i -ую чистую стратегию,
, а игрок А – i -ую чистую стратегию,  . Тогда средний выигрыш игрока В окажется равным
. Тогда средний выигрыш игрока В окажется равным
 при стратегии
при стратегии 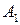 (60)
(60)
 при стратегии
при стратегии 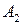 (61)
(61)
На плоскости qOz уравнения (60) и (61) описывают прямые III и IV
Очевидно, 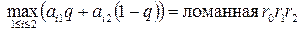 , которую называют верхней огибающей прямых III и IV.
, которую называют верхней огибающей прямых III и IV.
Нетрудно видеть, что 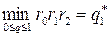
Таким образом, нижняя точка верхней огибающей –  определяет оптимальную стратегию игрока В:
определяет оптимальную стратегию игрока В: 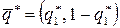 и цену игры
и цену игры  .
.
Для рассмотренной выше гры с матрицей H найдем стратегии игрока В.
На плоскости qOz построим две прямые, описываемые уравнениями:  и
и  или
или 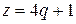 (III) и
(III) и  (IV).
(IV).
Решая систему уравнений
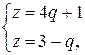
найдем 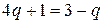 ,
,  ,
, 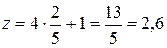 .
.
Таким образом, имеем  и
и 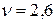 .
.
Замечания. На практике оптимальную стратегию игрока В, если оптимальная стратегия игрока А, следовательно, и цена игры известны, находят приравниванием любого из двух средних выйгрышей игрока В к цене игры:
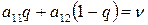 или
или  .
.
Для рассмотренного примера такими уравнениями будут
 или
или 
Аналогично находят оптимальную стратегию игрока А, если известна оптимальная стратегия игрока В.
Решают такие игры графическим способом, описанным выше. Отличие от  – игр заключается в следующем.
– игр заключается в следующем.
1) Нижняя (верхняя) огибающая семейства прямых


содержит большее число отрезков.
2) Пусть в игре  в верхней точке нижней огибающей пересекаются прямые
в верхней точке нижней огибающей пересекаются прямые  и
и  . Тогда при нахождении оптимальной смешанной стратегии игрока В согласно Теореме 2 полагают, что
. Тогда при нахождении оптимальной смешанной стратегии игрока В согласно Теореме 2 полагают, что 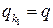 ,
, 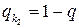 ,
,  ,
,  , где q – решение уравнения
, где q – решение уравнения
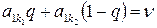 или
или 
3) Пусть в игре  в нижней точке верхней огибающей пересекаются прямые
в нижней точке верхней огибающей пересекаются прямые 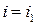 и
и  . Тогда при нахождении оптимальной смешанной стратегии игрока А согласно Теореме 2 полагают, что
. Тогда при нахождении оптимальной смешанной стратегии игрока А согласно Теореме 2 полагают, что  ,
,  ,
,  ,
,  , где p – решение уравнения
, где p – решение уравнения
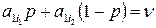 или
или  .
.
|
|
|
|
|
Дата добавления: 2014-12-25; Просмотров: 547; Нарушение авторских прав?; Мы поможем в написании вашей работы!