Основні властивості перетворення Лапласа. Реальні САК мають математичну модель у вигляді складних диференціальних рівнянь, розв’язок яких у загальному вигляді в більшості випадків неможливий

Реальні САК мають математичну модель у вигляді складних диференціальних рівнянь, розв’язок яких у загальному вигляді в більшості випадків неможливий. Для полегшення даної задачі розроблено декілька методів. Найбільш поширеним є метод перетворення Лапласа, побудований на тому, що функції часу замінюють їх зображеннями.

Перетворенням Лапласа називають співвідношення:

(5.6)

Це співвідношення ставить у відповідність функції x(t) дійсної змінної t функцію X(s) комплексної змінної s (s = s + jw).

При цьому x(t) називають оригіналом, а X(s) - зображенням за Лапласом. Це записують таким чином: x(t)® X(s), або X(s)® x(t).

Інколи використовують символічний запис: X(s)=L{x(t)}, де L - оператор Лапласа.

Співвідношення

(5.7)

визначає за відомим зображенням його оригінал і називається оберненим перетворенням Лапласа.

Символічно це можна записати так: x(t) = L^-1{X(s)}, де L^-1 – обернений оператор Лапласа.

Зупинимося на основних властивостях перетворення Лапласа.

Властивість лінійності. Для будь-яких постійних a і b справедливо:

L{ax₁(t) +bx₂(t)} = aL{x₁(t) + bL{x₂(t)}. (5.8)

Диференціювання оригіналу. Цю властивість запишемо з урахуванням нульових початкових умов, тобто x(0) = x'(0) = x''(0) = ….= 0:

(5.9)

Таким чином, за нульових початкових умов диференціюванню оригіналу відповідає множення зображення на s.

Інтегрування оригіналу. Інтегруванню оригіналу відповідає ділення зображення на s:

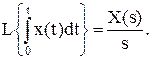(5.10)

Теорема запізнення. Для будь-якого додатного числа t:

(5.11)

Теорема згортки (теорема множення зображень).

(5.12)

Інтеграл у правій частині рівняння називають згорткою функцій x₁(t) і x₂(t) і позначають x₁(t) 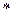x₂(t), тобто

L{x₁ (t) * x₂ (t)} = X₁(s)×X₂(s). (5.13)

Дата добавления: 2014-12-25