Теореми про граничні значення

(5.14)

Ці теореми дозволяють визначити усталене (кінцеве) або початкове значення функції х(t) за відомим зображенням.

Теорема розкладу. Теорема дозволяє знайти оригінал за відомим зображенням, яке являє собою дробово-раціональну функцію X(s) = A(s)/B(s), причому ступінь полінома чисельника менше ступеня полінома знаменника. Якщо всі корені рівняння B(s)=0 прості, то формула розкладу може бути записана у вигляді:

(5.15)

де n - ступінь полінома B(s); S_k - корені рівняння B(s) = 0.

Перетворення Лапласа є дуже цінним методом аналізу і синтезу систем керування, коли необхідно визначити перехідні процеси і точність регулювання в усталеному режимі. Але слід пам'ятати, що це перетворення є справедливим тільки для лінійних стаціонарних (з постійними параметрами) систем. У нестаціонарних системах один або декілька параметрів залежать від часу, тому перетворенням Лапласа користуватися не можна. Перетворення Лапласа не можна використовувати також для аналізу нелінійних систем.

У таблиці 5.1 наведені деякі важливі перетворення Лапласа.

Таблиця 5.1

Перетворення Лапласа найпростіших функцій

x(t)	X(s)	x(t)	X(s)	x(t)	X(s)
1(t)	1/s	t^2	2/s^3	sin(wt)	w/(s^2+w^2)
d(t)		t^n	n!/s^n+1	cos(wt)	s/(s^2+w^2)
d'(t)	s	e^-^a^t	1/(s+a)	e^-^a^t ×sin(wt)	w/[(s+a)^2+w^2]
t	1/s^2	t×e^-^a^t	1/(s+a)^2	e^-^a^t ×cos(wt)	(s+a)/[(s+a)^2+w^2]

5.3 Форми запису лінійних диференціальних рівнянь.

Передавальні функції

При описанні САК широко використовують символічну форму запису лінійних диференціальних рівнянь. Для цього вводять позначення p для операції диференціювання, тобто d/dt º p; dⁱ/dtⁱ º pⁱ.

З урахуванням цього рівняння (2.5) набуде вигляду:

a_n pⁿ y(t) + a_n-1 p^n-1y(t) + … +a₁py(t) + a₀y(t) =

= b_m p^mx(t)+ b_m-1 p^m-1x(t)+ … +b₁px(t)+ b₀x(t). (5.16)

При запису і перетворенні диференціальних рівнянь оператор p можна розглядати як алгебраїчний множник, а вираз py(t) - як добуток, що не володіє властивістю комутативності, тобто не можна записати y(t)p.

Винесемо x(t) і y(t) за дужки:

(a_n pⁿ + a_n-1 p^n-1 + … +a₁ p + a₀)×y(t) =

= (b_m p^m + b_m-1 p^m-1 + … +b₁ p + b₀)×x(t). (5.17)

Уведемо позначення:

Q(p) = a_n pⁿ + a_n-1 p^n-1 + … a₁ p + a₀ - власний оператор САК (оператор при вихідній величині);

R(p) = b_m p^m + b_m-1 p^m-1 + … b₁ p + b₀ - оператор впливу (оператор при вхідній величині).

Тоді рівняння (5.17) можна записати у вигляді:

Q(p)×y(t) = R(p)×x(t). (5.18)

Уведемо поняття передавальної функції.

Передавальною функцією в операторній формі називається відношення оператора впливу до власного оператора:

W(p) = R(p)/Q(p). (5.19)

Тоді рівняння системи може бути записано в більш компактній формі:

y(t) = W(p)×x(t) (5.20)

Рівняння (5.17), (5.18), (5.20) називають рівняннями в символічній або операторній формі запису.

У курсі ТАК прийнята стандартна форма запису лінійних диференціальних рівнянь, при якій члени, що містять вихідну величину та її похідні, записують у лівій частині рівняння, а решту членів - у правій частині. Коефіцієнт при вихідній величині y(t) роблять рівним одиниці.

Рівняння (5.5) може бути записано також в операційній формі, якщо до лівої та правої частин застосувати перетворення Лапласа:

(5.21)

або

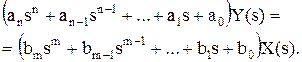(5.22)

Зовні рівняння (5.17) та (5.22) схожі, але вони принципово відрізняються одне від одного, оскільки в першому буква p позначає оператор диференціювання d/dt, а змінні x(t) та y(t) є реальними функціями часу. Тобто рівняння залишається диференціальним. Рівняння (5.22) - алгебраїчне. У ньому буква s позначає комплексу змінну, а величини X(s) і Y(s) є зображеннями фізичних величин x(t) та y(t).

Крім того, схожість даних рівнянь можлива, тільки якщо система стаціонарна, тобто коефіцієнти a_i, b_j постійні, а початкові умови для диференціального рівняння нульові.

Операційна форма запису рівнянь проста і зручна, оскільки перетворити та розв’язати алгебраїчне рівняння простіше, ніж диференціальне. Це забезпечило її широке застосування в теорії автоматичного керування.

Введемо поняття передавальної функції за Лапласом.

Передавальною функцією за Лапласом W(s) називається відношення зображення вихідної величини до зображення вхідної величини за нульових початкових умов.

Із (5.22) отримуємо:

(5.23)

Тоді рівняння (5.22) можна записати у вигляді

Y(s) = W(s)×X(s). (5.24)

Знаменник передавальної функції (2.23) є характеристичним поліномом системи. Якщо його прирівняти до нуля, отримаємо характеристичне рівняння САК, тобто

a_nsⁿ + a_n-1s^n-1 +…+ a₁s + a₀ = 0. (5.25)

Корені характеристичного рівняння визначають характер руху системи і називаються полюсами передавальної функції, а корені чисельника називаються нулями передавальної функції. У полюсах функція W(s) перетворюється на нескінченність, а в нулях вона стає рівною нулю. Розміщення полюсів на комплексній s-площині визначає характер власного (вільного) руху системи.

Передавальна функція системи W(s) та її часові функції h(t) i w(t) пов'язані між собою:

L{h(t)} = W(s)/s - зображення перехідної функції;

L{w(t)} = W(s) - зображення імпульсної перехідної функції.

Звідси, відповідно, можна записати:

w(t) = L^-1{W(s)}, h(t) = L^-1 {W(s)/s}. (5.26)

Співвідношення (5.26) дозволяють знайти перехідну та імпульсну перехідну функції САК за її відомою передавальною функцією W(s). Для цього можуть бути використані таблиці зображень основних елементарних функцій (додаток Е) чи теорема розкладу.

Дата добавления: 2014-12-25