Теория инженерного эксперимента

Инженерный эксперимент проводится для определения алгоритма функционирования (математической модели) объекта исследований.

Алгоритм функционирования – связи, закономерности, существующие между входными и выходными переменными объекта исследования.

Описывают объекты исследования в статических и динамических режимах. Для статических режимов алгоритмы функционирования называются статическими, а для переходных режимов динамическими.

Получение алгоритма функционирования объектов исследования возможно с помощью аналитических и экспериментальных методов. Аналитические базируются на известных фундаментальных законах. Экспериментальные называются идентификацией.

Рисунок 10:54 30.10.2014.

Для описания объекта исследования применяется полная математическая модель.

Статическая модель:

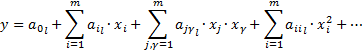
Обобщённый вид:

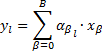
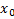– фиктивный фактор ();

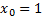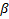– номер члена полинома ()

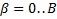Пример.

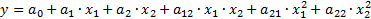
Если 1 вход:

Динамическая модель

Рисунок 11:25 30.10.2014.

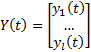
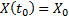
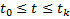
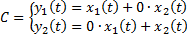
– матрица коэффициентов.

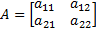
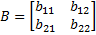
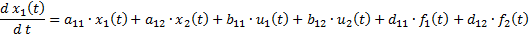
По частоте:

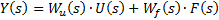
– матричная функция по каналу управления;

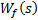– матричная передаточная функция по каналу возмущения.

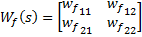
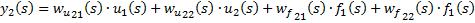
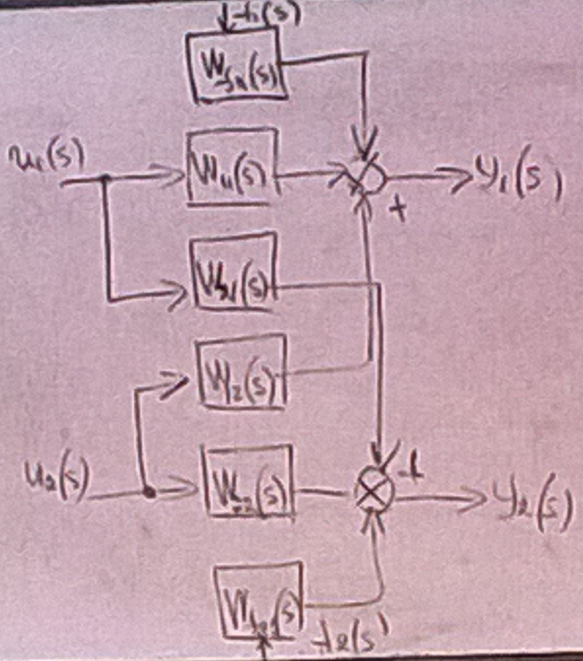
Рисунок 11:47 30.10.2014.

Статическая идентификация

Для идентификации одномерных объектов в установившихся режимов (статических) применяются метод корреляционного и регрессионного анализа.

Рисунок 10:35 06.11.2014 – Одномерный ОИ.

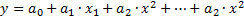
Позволяет определить вид модели и коэффициент.

Для определения вида модели применяется метод корреляционного анализа. Для определения коэффициентов модели применяется метод регрессионного анализа.

1. Метод корреляционного анализа.

1) строится корреляционное поле ;

2) ос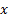и и разбиваются на одинаковые отрезки;

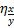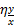3) определяются корреляционные отношения Пирсона и :

и 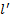– число равных интервалов, на которое разбивается ось 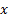и ;

и - число наблюдений, попавших в j-ый интервал;

и – условное среднее значение на интервале;

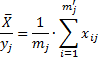
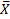и – среднее значение переменных.

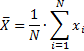
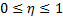
если 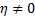, то связь существует и нужно определить связь.

4) для определения степени полинома оценивают разность ординат.

				…
				…
				…

:

:

:

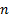
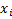
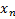
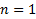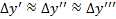
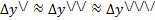
5) определяется коэффициент корреляции:

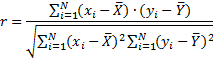
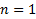– связь линейная:

2. Метод регрессионного анализа.

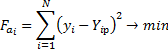
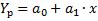
– экспериментальные значения;

– вычисленные значения.

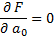
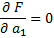
и так далее.

6) коэффициенты определяются:

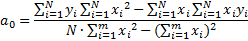
7.1) проверка полученной модели на адекватность.

				…
				…
				…
				…

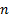
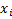
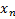
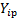
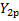
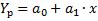
7.2) определяем среднеквадратичное отклонение:

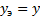
7.3) заключение: полученная математическая модель вида адекватна реальному объекту с точностью 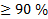; если больше 90 %, то нужно было выбрать модель боле высокой степени полинома.

Статическая идентификация многомерных объектов исследования

Рисунок 11:20 06.11.2014 – 2 входа и 1 выход.

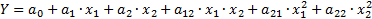
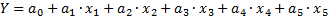
Есть метод пассивного эксперимента или множественного регрессионного анализа.

1) составляется матрица наблюдений:

Фактор	Выходная переменная
…	…	…	…	…	…

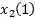
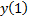
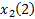
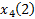
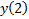
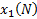
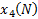
2) для определения коэффициентов модели, точно так же, как и в 1-ом случае, записывается функционал:

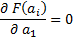
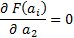
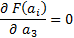
Отсюда находим , , , .

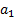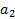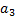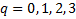
Общий вид:

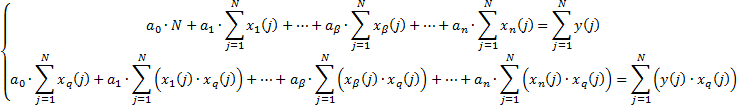
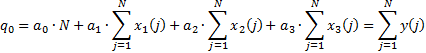
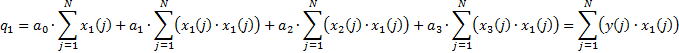
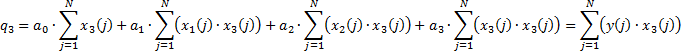
3) проверяем модель на адекватность:

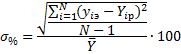
3.3) заключение: полученная математическая модель вида 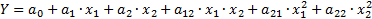адекватна реальному объекту с точностью 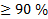; если больше 90 %, то нужно было выбрать модель боле высокой степени полинома.

Метод активного планирования эксперимента

Основным для этого метода является матрица планирования.

1. 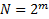, – число формируемых факторов.

N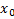
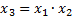
		+1	+1	+1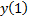
		-1	+1	-1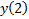
		+1	-1	-1
		-1	-1	+1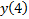

– значение переменной в абсолютных единицах;

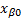– начальный уровень входной переменной, соответствует номинальному режиму;

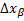– интервал изменения.

Интервал изменения выбирают так и таким образом, чтобы верхний уровень фактора в относительных единицах должен быть равен +1, а нижний уровень -1.

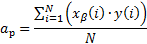
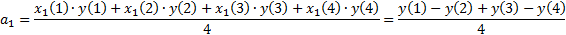
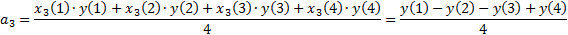
Пример. Найти , , , .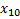

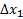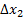N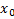
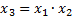
	+1	+1	+1	+1
	+1	-1	+1	-1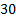
	+1	+1	-1	-1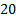
	+1	-1	-1	+1

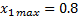
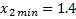
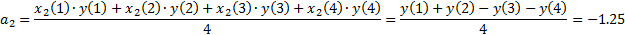
Проверяем расчётные значения:

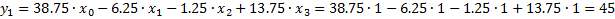
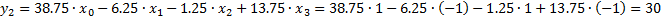
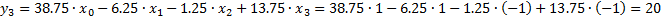
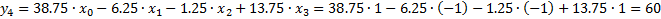
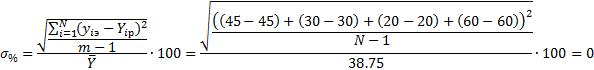
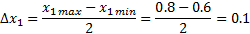
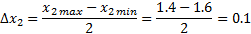
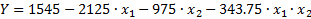
Проверка:

Строка 1:

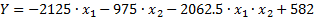
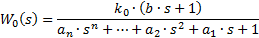
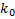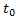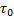, , – данные параметров ОИ.

Графо-аналитический метод

1. Построение кривой разгона.

			…
			…
			…

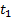
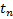
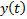
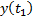
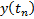
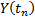
Рисунок 11:30 20.11.2014.

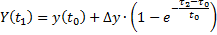
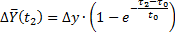
		0.067	0.3(3)	0.7	0.9
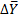
			0.22	0.53	0.72	0.83

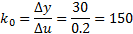
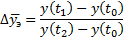
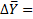
Рисунок 11:48 20.11.2014.

При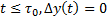

Адекватность:

14 %.

Определение динамических параметров объекта исследования. Метод площадей трапеций.

1. Графоаналитический метод.

Из графика определяются 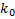, и .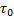

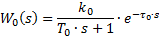
2. Метод площадей трапеции.

			…
			…

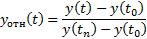
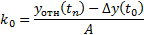
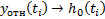
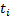
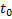
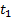
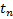
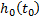
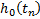
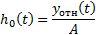
Чтобы найт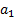и и 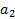нужно определить 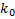, 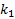и .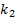

…	…	…	…	…	…	…	…

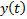
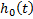
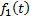
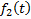
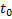
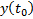
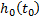
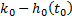
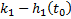
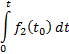
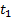
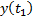
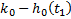
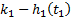
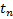
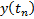
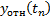
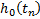
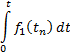
Последние значение :

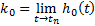
Это

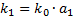
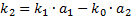
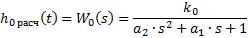
3. Метод площадей Симою.

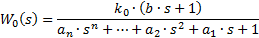
Применяется для динамической идентификации объекта исследования.

…	…	…	…	…	…	…

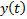
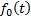
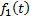
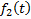
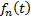
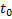
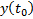
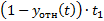
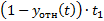
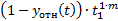
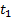
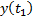
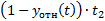
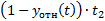
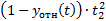
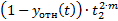
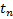
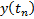
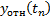
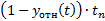
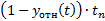
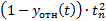
Согласно методу, находятся суммы:

…

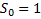
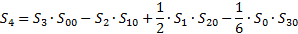
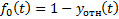
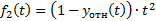
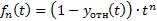
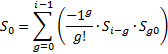
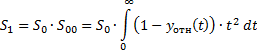
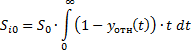
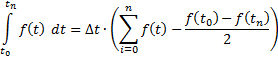
Расчёты прекращают при .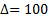

При 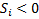, то:

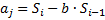
Экспертные оценки в инженерных исследованиях

Метод экспертных оценок для принятия решения. 1 из методов получения объективной информации от группы специалистов является метод экспертных оценок. Состоит из нескольких этапов:

1. Подбор группы специалистов.

Рассмотрение компетентных лиц, которые служат основой для выбора экспертов.

2. Составление анкет.

Один из способов отбора, отвечая на вопросы которых, кандидат в эксперты должен показать свою эрудицию. Анкета позволяет судить о действительных знаниях эксперта.

3. Проведение опроса.

Ещё один из способов расчёт достоверности и точности их оценок. Отношение

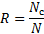
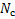– число случаев, в которых случаев эксперт предписал вероятность той гипотезе, которая оказалась верной.

– общее число случаев, когда эксперт производил оценку.

– степень надёжности для группы экспертов.

4. Анализ и обработка полученной информации.

Делается всё так:

1. Выбор модели объекта.

Выбор базовой модели и количество .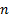

2. Расчёт относительных показателей .

Показатели моделей сравниваются с показателями базовой модели.

3. Определение весовых коэффициентов показателей.

Весовые коэффициенты каждой группы.

4. Определение суммарного обобщённого показателя группы.

5. Расчёт обобщённых показателей групп с учётом весовых коэффициентов.

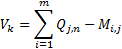
Пример. Исследуется 3 объекта (машины в пример). Модель А, Б, В.

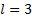
Исследуются следующие группы показателей:

1) размеро-весовые ();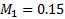

2) назначение ();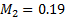

3) надёжность ();

4) экономическая эксплуатация ();

5) эргономика кабины водителя ();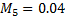

6) эргономика салона ();

7) экологические показатели ();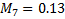

8) эстетические ().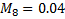

Расчёт обобщённых показателей объектов.

Группа показателей по 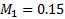. Б принимаем базовым.

Наименование показателя	Значение	Относительное значение	Коэффициент весомости	Обобщённый показатель
А	Б	В	А	Б	В	А	Б	В
Вместимость				0.5		0.75	0.38	0.19	0.38	0.28
Полная масса, кг				0.59		0.93	0.38	0.22	0.38	0.35
Максимальная осевая нагрузка, кг				0.49		1.04	0.06	0.03	0.06	0.06
Объектов на человека, ед/кг				1.18		1.24	0.18	0.21	0.18	0.22
								0.65		0.91

Дата добавления: 2014-12-25