Симплексний метод

Розв’язання ЗЛП геометричним методом є наочним у випадку двох змінних. Для випадку ж більшої кількості змінних геометричний метод стає неможливим. Так званий симплекс-метод належить до числа аналітичних і є універсальним методом, яким можливо розв’язати будь-яку ЗЛП.

Ідея симплексного методу полягає у наступному. Використовуючи систему обмежень, приведену до канонічного вигляду, тобто до системи лінійних рівнянь, знаходять її будь-який базисний розв’язок. Якщо цей розв’язок є допустимим, то перевіряють його на оптимальність. Якщо він є неоптимальним, то переходять до іншого допустимого базисного розв’язку. Симплексний метод гарантує, що при цьому новому розв’язку цільова функція якщо і не досягне оптимуму, то наблизиться до нього. Продовжують таку дію, доки не отримають оптимальний розв’язок.

Якщо перший базисний розв’язок виявиться недопустимим, то за допомогою симплекс-методу здійснюється перехід до іншого базисного розв’язку, який дозволяє наблизитись до області допустимих розв’язків, доки на якомусь кроці не отримаємо допустимий базисний розв’язок. Після цього застосовують попередній механізм симплексного методу.

Таким чином, застосування симплексного методу розпадається на два етапи: 1) знаходження допустимого базисного розв’язку системи обмежень; 2) знаходження оптимального розв’язку. При цьому кожний етап може містити кілька кроків, відповідних тому або іншому базисному розв’язку. Оскільки число базисних розв’язків завжди обмежено, то обмежено і число кроків симплекс-методу.

Прослідкуємо ідею методу на прикладі.

Приклад 5.

Розглянемо ЗЛП у канонічному вигляді

, .

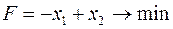
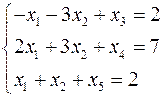
Оберемо за базисні змінні 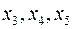та виразимо їх через вільні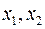

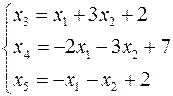(12)

Так як , то найменші значення 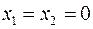, при цьому 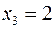, , 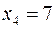, 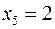тобто цей базисний розв’язок є допустимим. Значення цільової функції в цьому розв’язку 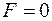. Чи можна за рахунок збільшення 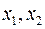зменшити ? Так, якщо збільшувати змінну 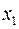, бо вона входить до виразу зі знаком «–». Збільшення ж змінної напроти призведе до збільшення , бо перед цією змінною знак «+», тому залишимо . Необмежено збільшувати 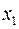неможна, бо розв’язок перестане бути допустимим. Якщо застосувати умову невід’ємності змінних до (12) та врахувати , отримуємо систему

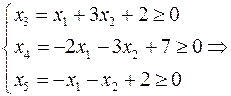
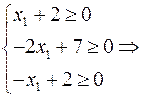
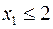
Найбільше можливе значення , при цьому 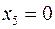, тобто 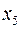стає вільною змінною, а – базисною. Отримуємо новий допустимий базисний розв’язок 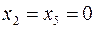, , , 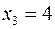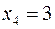. Значення цільової функції при цьому 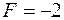, тобто зменшилося. Розглянемо, як виглядає вираз через 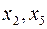. Для цього виразимо з третього рівняння (12) 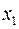через нові вільні змінні 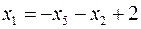і підставимо до виразу цільової функції . Так як обидві змінні входять до виразу зі знаком «+», ще зменшити значення неможливо, тобто ми досягли оптимального розв’язку.

Розглянуті вище дії (перехід від одного базисного розв’язку до іншого) можна проводити у таблиці за допомогою алгоритму Жордана-Гауса.

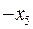
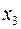
	–1	–3		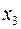		–2
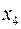
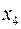
					–2
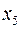
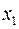
		–1			–1	–2	–2

Правила вибору розв’язуючого елемента (тобто змінних, які переходять з вільних у базисні та навпаки), які були проілюстровані у прикладі, можна формалізувати у вигляді алгоритму симплекс-методу:

0 крок. Записуємо ЗЛП у канонічному вигляді, обираємо будь-які базисні змінні та виражаємо їх через вільні. Складаємо симплекс-таблицю – таблицю коефіцієнтів виразу базисних змінних та цільової функції через вільні змінні. Якщо відповідний базисний розв’язок не є допустимим, переходимо до іншого базисного розв’язку (алгоритм цього переходу опишемо пізніше).

1 крок. Перевіряємо критерій оптимальності: в рядку коефіцієнти при вільних змінних недодатні. Якщо критерій оптимальності не виконаний, обираємо розв’язуючий елемент наступним чином:

а) в рядку обираємо найбільший за абсолютною величиною додатній коефіцієнт при вільних змінних – він визначає розв’язуючий стовпчик;

б) складаємо невід’ємні відношення елементів останнього стовпчика до відповідних елементів розв’язуючого стовпчика та обираємо серед них найменше – це визначає розв’язуючий рядок.

2 крок. Виконуємо алгоритм Жордана-Гауса з обраним розв’язуючим елементом.

Повторюємо кроки 1 і 2, доки критерій оптимальності не буде виконаним.

Зауваження. Якщо розв’язується задача на знаходження максимуму цільової функції, критерій оптимальності змінюється на такий: в рядку коефіцієнти при вільних змінних невід’ємні. Також змінюється правило вибору розв’язуючого стовпчика: в рядку обираємо найбільший за абсолютною величиною від’ємний елемент. Інші кроки алгоритму залишаються незмінними.

Приклад 6.

Розв’яжемо симплексним методом задачу про використання сировини, яка задана формулами (6), (7). Приведемо систему обмежень до канонічного вигляду:

Виразимо базисні змінні 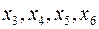через вільні 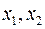(це найпростіший вибір)

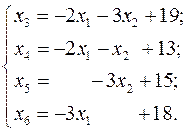
Заносимо коефіцієнти у симплекс-таблицю

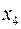
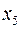
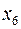
	–7	–5

Відповідний базисний розв’язок 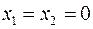, , 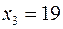, , 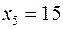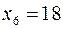є допустимим, 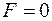. Критерій оптимальності (див. зауваження) не виконаний (7 і 5 – від’ємні). Обираємо розв’язуючий стовпчик 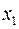(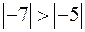; 7>5), знаходимо 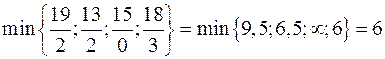, тобто розв’язуючий рядок 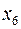. Виконавши алгоритм Жордана-Гауса, отримуємо таблицю

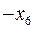
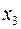
	–2/3
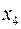
	–2/3
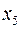
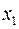
	1/3
	7/3	–5

Відповідний базисний розв’язок 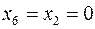, , , , 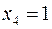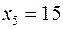є допустимим, 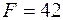. Критерій оптимальності не виконаний (–5 – від’ємне). Обираємо розв’язуючий стовпчик (інших додатних елементів у рядку немає), знаходимо 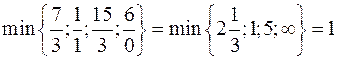, тобто розв’язуючий рядок 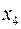. Виконавши ще раз алгоритм Жордана-Гауса, отримуємо таблицю

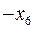
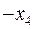
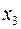
	4/3	–3
	–2/3
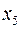
		–3
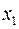
	1/3
	–1

Відповідний базисний розв’язок 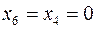, , 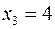, , 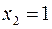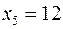є допустимим, 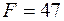. Критерій оптимальності не виконаний (–1 – від’ємне). Обираємо розв’язуючий стовпчик 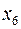(інших додатних елементів у рядку немає), знаходимо 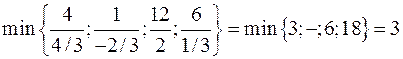, тобто розв’язуючий рядок 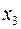. Виконавши ще раз алгоритм Жордана-Гауса, отримуємо таблицю

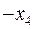
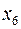
	3/4	–9/4
	1/2	–1/2
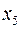
	–3/2	3/2
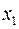
	–1/4	3/4
	3/4	11/4

Відповідний базисний розв’язок , , 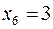, , 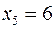є допустимим, . Критерій оптимальності виконаний, тобто розв’язок задачі .

Відмітимо, що під час переходу від одного базисного розв’язку до іншого значення цільової функції тільки збільшувалося, тобто ми поступово наближалися до максимуму.

Порівняємо процес розв’язання задачі симплекс-методом з геометричним розв’язанням. Вихідний базисний розв’язок 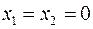відповідає точці О області допустимих розв’язків (див. рис. 4). Наступний розв’язок , – це вершина А шестикутника. Далі ми отримуємо вершину В(6;1) і, нарешті, приходимо до оптимального розв’язку – точка С(5;3). Увесь час ми переходимо від однієї вершини многокутника до сусідньої, розташованої у напрямку найбільшого зростання цільової функції.

Під час розв’язання ЗЛП симплекс-методом можуть виникнути такі ускладнення:

1) процес переходу від однієї таблиці до іншої переривається, хоча оптимальний розв’язок не досягнутий. Перешкода виникає при виборі розв’язуючого рядка – не існує невід’ємних елементів у вибраному розв’язуючому стовпчику і, як наслідок, неможливо скласти невід’ємні відношення елементів останнього стовпчика до відповідних елементів розв’язуючого стовпчика. Це означає, що така ЗЛП не має оптимального розв’язку (область допустимих розв’язків і цільова функція на ній необмежені).

2) оптимальний розв’язок не досягається, хоча при переході немає перешкод (зациклення). В цьому випадку потрібно ще раз розглянути таблицю, з якої почався цикл і обрати інший розв’язуючий стовпчик.

Дата добавления: 2014-12-25