Побудова правильного відсікання

Алгоритм методу Гоморі.

1. Розв’язуємо симплекс-методом ЗЛП без умови цілочисельності.

2. Якщо оптимальний розв’язок є цілочисельним, то знайдений розв’язок збігається з оптимальним розв’язком задачі цілочисельного програмування.

3. Якщо серед компонент оптимального плану є хоча б одна нецілочисельна, то до обмежень задачі додається нове обмеження з властивостями:

1) лінійне;

2) відсікає знайдений оптимальний нецілочисельний план;

3) не відсікає жодного цілочисельного плану.

Додаткове обмеження з вказаними особливостями називається правильним відсіканням. Розв’язуємо двоїстим симплекс-методом ЗЛП з додатковим обмеженням.

Процес побудови додаткових обмежень продовжується доти, доки не буде отримано цілочисельний план або виявиться відсутність цілочисельного розв’язку задачі.

Введемо такі позначення:

– ціла частина числа , найбільше ціле число, яке не перевершує . Наприклад, , , .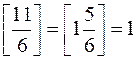

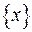– дробова частина числа , , .

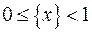Наприклад, , , .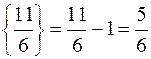

Відсікання Гоморі обирають наступним чином: серед нецілочисельних розв’язків системи обирають компоненту з максимальною дробовою частиною та з відповідного рівняння формують правильне відсікання

.

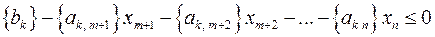Вводимо нову змінну 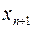. Отримали розширену симплекс-таблицю, в якій в стовпці вільних членів є від’ємне число. Розв’язуємо цю задачу симплекс-методом. Якщо розв’язок не є цілочисельним, повторюємо алгоритм знову.

Приклад 10.

					1/3	5/3	17/3
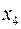
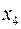
	–2				2/3	34/3	34/3

Розв’язок знайдений, але він не є цілочисельним. Максимальна дробова частина , будуємо додаткове відсікання за першою строкою.

,

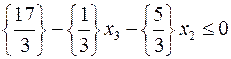обчислюємо дробові частини

,

,

.

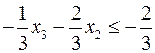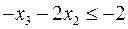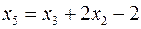Заносимо додаткове обмеження в таблицю і розв’язуємо двоїстим симплекс-методом.

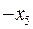
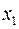
	1/3	5/3	17/3		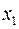1/3
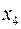
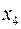
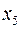
	–1	–2	–2		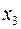–1
	2/3	34/3	34/3

Розв’язок є оптимальним і цілочисельним.

Відповідь: .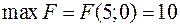

Тема 3. Транспортна задача.

(методичні вказівки № 1358, стор. 34-46)

Серед задач лінійного програмування, до яких зводиться аналіз практичних моделей управління і планування, можна виділити ряд класів задач, системи обмежень яких мають певні структурні особливості.

Серед спеціальних задач, на практиці частіше за інші зустрічається транспортна задача, різні її модифікації та узагальнення. Класична транспортна задача – задача про найдешевший план перевезення однорідного продукту чи взаємозамінних продуктів з пунктів виробництва в пункти споживання. Розглянемо транспортну задачу за критерієм вартості.

Нехай на станціях зосереджено 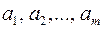одиниць деякого однорідного вантажу. Цей вантаж треба перевезти в пунктів призначення 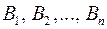, причому в кожен з них потрібно завезти відповідно 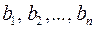одиниць цього вантажу. Вартість перевезення одиниці вантажу з пункту 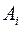у пункт 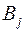(тариф) дорівнює і вважається заданою. Потрібно скласти такий план перевезення, щоб його загальна вартість була мінімальною. Якщо загальний запас вантажу на всіх станціях відправлення дорівнює загальній сумі потреб усіх пунктів, тобто

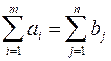, (13)

то таку задачу називають транспортною задачею з правильним балансом (або закритою транспортною задачею). Якщо умова (13) порушується, її називають транспортною задачею з неправильним балансом (або відкритою транспортною задачею). Відкрита транспортна задача потребує введення умовного постачальника або споживача. Якщо 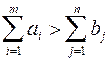, то вводять умовного споживача 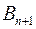з потребою у вантажі 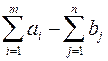та нульовою вартістю перевезення , 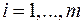а якщо , то вводять умовного постачальника 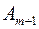з потребою у вантажі та , .

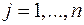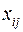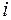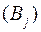Позначимо – кількість товару, перевезеного з -го пункту виробництва в -й пункт споживання . Припустимо, що виконується умова балансу (13). Запишемо задачу у вигляді таблиці.

Таблиця 3.

			…
		…
				…
				…
…	…	…	…	…	…
				…

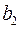
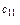
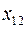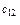
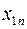
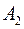
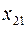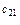
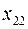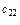
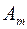
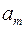
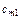
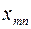
Із таблиці 3 видно, що кількості товару, перевезеного з першого, другого,…, -го пунктів виробництва, відповідно, задовольняють умови

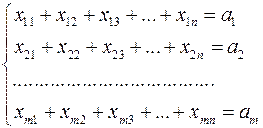
Звернемо увагу на те, що змінні та права частина рівнянь взяті з одного рядка матриці перевезень. Через це будемо називати ці рівняння горизонтальними рівняннями.

Кількості товару, що ввозиться в перший, другий,…, -й пункт споживання, відповідно, задовольняють умови

Змінні та права частина рівнянь взяті з одного стовпця матриці перевезень. Через це ми будемо називати їх вертикальними рівняннями.

Загальна вартість усіх перевезень виражається формулою

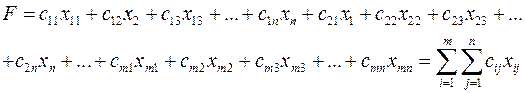
Отже, математична модель цієї задачі має такий вигляд: треба знайти мінімальне значення функції

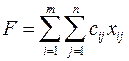
при умовах

Оскільки транспортна задача – це ЗЛП, її можна розв’язати симплекс-методом. Однак через просту будову системи обмежень симплекс-метод тут набагато спрощується.

Дата добавления: 2014-12-25