
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
МЕХАНИКА 1 страница
|
|
|
|
1.1 Радиус вектор частицы зависит от времени по закону: а) 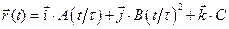 б)
б)  в)
в) 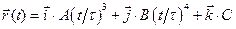 Найдите тангенс угла между вектором скорости
Найдите тангенс угла между вектором скорости  и а) осью X б) осью y. а)
и а) осью X б) осью y. а) 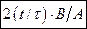
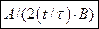 б)
б) 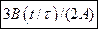
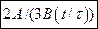
в) 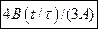
 .
.
1.2 Радиус … а) 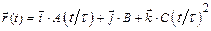 б)
б)  в)
в) 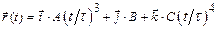 Найдите тангенс угла между вектором скорости
Найдите тангенс угла между вектором скорости  и А) осью X б) осью y
и А) осью X б) осью y
а) 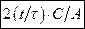
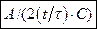 . б)
. б) 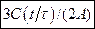
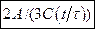 . в)
. в) 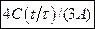
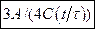 .
.
1.3 Радиус вектор частицы зависит от времени по закону 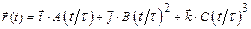 На каком расстоянии будет находится частица а) от оси x б) от оси y в) от оси z
На каком расстоянии будет находится частица а) от оси x б) от оси y в) от оси z
а) 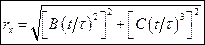 б)
б) 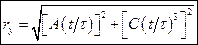 в)
в) 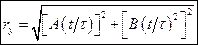 .
.
1.4 Радиус вектор частицы зависит от времени по закону а) 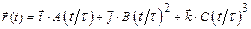
б)  Чему будет равна величина скорости частицы
Чему будет равна величина скорости частицы
а)  . б)
. б) 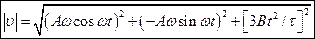 .
.
1.5 Радиус вектор частицы зависит от времени по закону  . Чему будет равна величина начальной скорости частицы
. Чему будет равна величина начальной скорости частицы 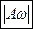 .
.
1.6 Радиус вектор частицы зависит от времени по закону 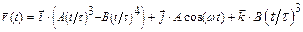 . Через сколько секунд перпендикулярной оси x окажется а) скорость частицы б) ускорение частицы. а)
. Через сколько секунд перпендикулярной оси x окажется а) скорость частицы б) ускорение частицы. а)  . б)
. б) 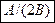 .
.
1.7 Радиус-вектор частицы зависит от времени по закону 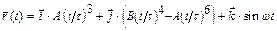 Через сколько секунд скорость частицы окажется перпендикулярной оси y
Через сколько секунд скорость частицы окажется перпендикулярной оси y 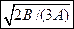 .
.
1.8 Радиус-вектор частицы зависит от времени по закону  . Через сколько секунд окажется перпендикулярной оси z а) скорость частицы б) ускорение частицы. а)
. Через сколько секунд окажется перпендикулярной оси z а) скорость частицы б) ускорение частицы. а) 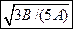 б)
б) 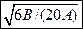 .
.
1.9 Через сколько секунд ускорение частицы будет перпендикулярно оси y если радиус-вектор частицы зависит от времени по закону 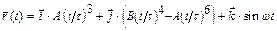
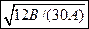 .
.
1.10 Скорость частицы зависит от времени по закону 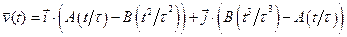 . Через сколько секунд ускорение частицы будет а)параллельно оси x б) перпендикулярно оси x в) перпендикулярно оси y:
. Через сколько секунд ускорение частицы будет а)параллельно оси x б) перпендикулярно оси x в) перпендикулярно оси y:
а) 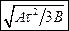 . б)
. б)  . в)
. в) 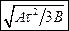 .
.
1.11 Скорость частицы зависит от времени как  а) через сколько секунд ускорение частицы будет направленно под углом 45 к оси x б) Чему станет равна величина полного ускорения частицы в момент времени
а) через сколько секунд ускорение частицы будет направленно под углом 45 к оси x б) Чему станет равна величина полного ускорения частицы в момент времени
а) 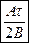 . б)
. б)  .
.
1.12 Скорость частицы зависит от времени по закону 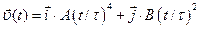 через сколько секунд ускорение частицы будет направленно под углом 45 к оси y.
через сколько секунд ускорение частицы будет направленно под углом 45 к оси y.  .
.
2.1 Частица начала свое движение из начала координат, и ее скорость зависит от времени по закону а) 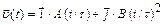 б)
б) 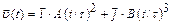 в)
в) 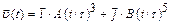 На какое расстояние от начала координат удалится частица а)
На какое расстояние от начала координат удалится частица а) 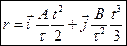 . б)
. б) 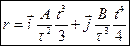 . в)
. в)  .
.
2.2 Частица начала свое движение из начала координат, и ее скорость зависит от времени по закону а) 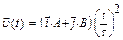 б)
б)  в)
в)  .Какой путь пройдет частица
.Какой путь пройдет частица
а) 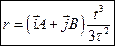 . б)
. б)  . в)
. в) 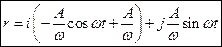 .
.
2.3 Частица начала свое движение из начала координат с нулевой начальной скоростью, и ее ускорение зависит от времени по закону а)  б)
б)  .Найти модуль скорости частицы а)
.Найти модуль скорости частицы а) 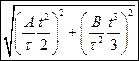 . б)
. б) 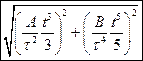 .
.
2.4 Частица начала свое движение из начала координат с нулевой начальной скоростью, и ее ускорение зависит от времени по закону. 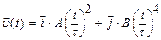 .Найти тангенс угла, под которым будет направлена скорость частицы а) к оси x б) к оси y.
.Найти тангенс угла, под которым будет направлена скорость частицы а) к оси x б) к оси y.
а) 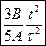 . б)
. б) 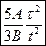 .
.
2.5 Частица начала свое движение из начала координат с начальной скоростью 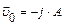 и с ускорением которое зависит от времени по закону а)
и с ускорением которое зависит от времени по закону а)  б)
б) 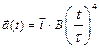 .Каков модуль скорости частицы а)
.Каков модуль скорости частицы а) 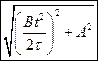 . б)
. б) 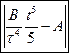 .
.
2.6 Частица начала свое движение из начала координат с начальной скоростью 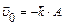 и с ускорением, которое зависит от времени по закону а)
и с ускорением, которое зависит от времени по закону а)  .Каков модуль скорости частицы а)
.Каков модуль скорости частицы а) 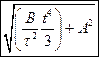 .
.
2.7 Частица начала свое движение из начала координат с начальной скоростью а)  б)
б) 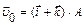 и с ускорением, которое зависит от времени по закону
и с ускорением, которое зависит от времени по закону 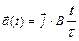 .Каков модуль скорости частицы а)
.Каков модуль скорости частицы а) 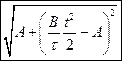 . б)
. б) 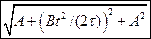 .
.
2.8 Частица начала свое движение из точки с радиус вектором а) 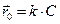 ; б)
; б) 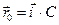 ; в)
; в) 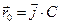 ;
;
г) 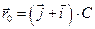 ; д)
; д) 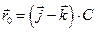 со скоростью, которая зависит от времени по закону
со скоростью, которая зависит от времени по закону  . На какое расстояние от начала координат удалится частица а)
. На какое расстояние от начала координат удалится частица а) 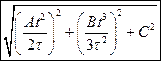 . б)
. б) 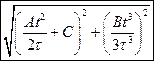 .
.
в) 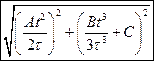 . г)
. г) 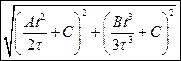 . д)
. д) 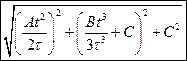 .
.
2.9 Частица начала сове движение из начала координат, и ее скорость зависит от времени по закону а) 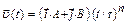 . Какой путь проделает частица
. Какой путь проделает частица 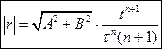 .
.
2.10 Частица начала свое движение из начала координат с нулевой начальной скоростью, и ее ускорение зависит от времени по закону 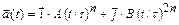 . Какая величина скорости будет у частицы в момент времени
. Какая величина скорости будет у частицы в момент времени 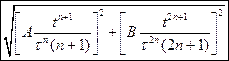 .
.
2.11 Частица начала свое движение из начала координат с начальной скоростью 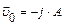 и с ускорением, которое зависит от времени по закону а)
и с ускорением, которое зависит от времени по закону а) 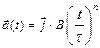 . Каков модуль скорости частицы
. Каков модуль скорости частицы  .
.
2.12 Частица начала свое движение из начала координат с начальной скоростью 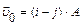 и с ускорением, к-рое зависит от времени по закону а)
и с ускорением, к-рое зависит от времени по закону а) 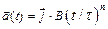 .Каков модуль скорости частицы в момент времени
.Каков модуль скорости частицы в момент времени  .
.
2.13 Частица начала свое движение из начала координат с начальной скоростью 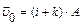 и с ускорением, которое зависит от времени по закону а)
и с ускорением, которое зависит от времени по закону а) 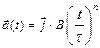 . Каков модуль скорости частицы в момент времени
. Каков модуль скорости частицы в момент времени 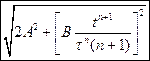
2.14 Частица начала свое движение из точки с радиус-вектором 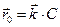 со скоростью, которая зависит от времени по закону а)
со скоростью, которая зависит от времени по закону а) 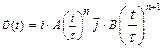 . На к-е. расст. от нач. коорд-т удалится частица
. На к-е. расст. от нач. коорд-т удалится частица 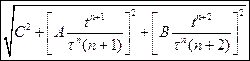 .
.
2.15 Частица начала свое движение из точки с радиус-вектором 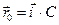 со скоростью, которая зависит от времени по закону а)
со скоростью, которая зависит от времени по закону а) 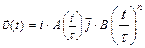 . На какое расстояние от начала координат удалится частица
. На какое расстояние от начала координат удалится частица  .
.
2.16 Частица начала свое движение из точки с радиус-вектором 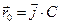 со скоростью, которая зависит от времени по закону а)
со скоростью, которая зависит от времени по закону а) 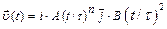 . На какое расстояние от начала координат удалится частица в момент времени
. На какое расстояние от начала координат удалится частица в момент времени 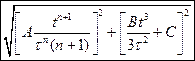 .
.
2.17 Частица начала свое движение из точки с радиус-вектором 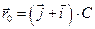 со скоростью, к-рая зависит от времени по
со скоростью, к-рая зависит от времени по
з-ну а)  . На к-е. расст. от начала корд-т удалится частица
. На к-е. расст. от начала корд-т удалится частица  .
.
2.18 Частица начала свое движение из точки с радиус-вектором 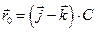 со скоростью, которая зависит от времени по закону а)
со скоростью, которая зависит от времени по закону а) 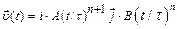 . На какое расстояние от начала координат удалится частица
. На какое расстояние от начала координат удалится частица 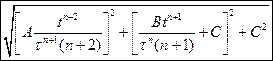 .
.
3.1 Частица из состояния покоя начала двигаться по дуге окружности радиуса R=1 м с постоянным угловым ускорением 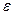 =1 с-1 Найти а) отношение тангенциального и нормального ускорения б) тангенс угла между вектором полного ускорения и вектором скорости частицы через время а)
=1 с-1 Найти а) отношение тангенциального и нормального ускорения б) тангенс угла между вектором полного ускорения и вектором скорости частицы через время а)  . б)
. б)  .
.
3.2 Частица из состояния покоя начала двигаться по дуге окружности радиуса R=1 со скоростью, модуль которой зависит от времени по закону  Найти а) тангенс угла между вектором полного ускорения и вектором скорости частицы а)
Найти а) тангенс угла между вектором полного ускорения и вектором скорости частицы а) 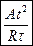 . б)
. б) 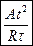 .
.
3.3 Частица из состояния покоя начала двигаться по дуге окружности радиуса R=1 с угловой скоростью, модуль которой зависит от времени по закону 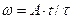 . Найти отношение нормального и тангенциального ускорения частицы:
. Найти отношение нормального и тангенциального ускорения частицы: 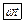 .
.
3.4 Частица из состояния покоя начала двигаться по дуге окружности радиуса R=1 с угловой скоростью, модуль которой зависит от времени по закону а) 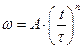 . Через сколько секунд угол между полным ускорением частицы и ее скоростью будет равен 45.
. Через сколько секунд угол между полным ускорением частицы и ее скоростью будет равен 45. 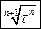 .
.
3.5 Частица из состояния покоя начала двигаться по дуге окружности радиуса R=1 так, что угол поворота зависит от времени по закону а)  . Найти линейную скорость частицы
. Найти линейную скорость частицы  .
.
3.6 Частица из состояния покоя начала двигаться по дуге окружности радиуса R=1 так, что угол поворота зависит от времени по закону а)  . Найти нормальное ускорение частицы
. Найти нормальное ускорение частицы  .
.
3.7 Частица из состояния покоя начала двигаться по дуге окружности радиуса R=1 так, что угол поворота зависит от времени по закону а)  . Найти тангенциальное ускорение частицы
. Найти тангенциальное ускорение частицы 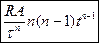 .
.
3.8 Частица из состояния покоя начала двигаться по дуге окружности радиуса R=1 с угловым ускорением, которое зависит от времени по закону а)  . Найти нормальное ускорение частицы
. Найти нормальное ускорение частицы 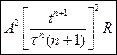 .
.
3.9 Частица из состояния покоя начала двигаться по дуге окружности радиуса R=1 с угловым ускорением, которое зависит от времени по закону а)  . Найти линейную скорость частицы
. Найти линейную скорость частицы 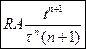 .
.
4.1 Диск радиуса R=1 начал вращаться вокруг своей оси без начальной скорости с угловым ускорением, зависящем от времени по закону а)  . На какой угол (в радианах) он повернется
. На какой угол (в радианах) он повернется  .
.
4.2 Диск радиуса R=1 вращался вокруг своей оси с угловой скоростью  . В момент времени
. В момент времени 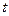 его угловое ускорение стало возрастать по закону а)
его угловое ускорение стало возрастать по закону а)  . Какую угловую скорость будет иметь диск
. Какую угловую скорость будет иметь диск  .
.
4.3 Диск радиуса R=1 вращался вокруг своей оси с угловой скоростью  . В момент времени
. В момент времени 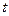 начал тормозить. Модуль его углового ускорения при этом зависел от времени по закону. а)
начал тормозить. Модуль его углового ускорения при этом зависел от времени по закону. а) 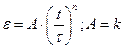 . Через сколько секунд диск остановится
. Через сколько секунд диск остановится 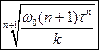 .
.
4.4 Диск радиуса R=1 начал вращаться вокруг своей оси так, что угол его поворота зависит от времени по закону а)  . Через сколько секунд диск остановится.
. Через сколько секунд диск остановится. 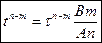 .
.
4.5 Диск радиуса R=1 вращался вокруг своей оси с угловой скоростью  . В момент времени t=0 его угловое ускорение стало возрастать по закону а)
. В момент времени t=0 его угловое ускорение стало возрастать по закону а)  . Через сколько секунд диск будет иметь максимальную угловую скорость.
. Через сколько секунд диск будет иметь максимальную угловую скорость. 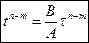 .
.
4.6 Диск... Посчитать площадь под графиками.
4.7 Диск... Посчитать площадь под графиками.
4.8 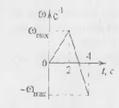 Диск вращается с угловой скоростью, зависимость от времени которой задается графиком. Найти максимальный угол поворота диска (в радианах) в интервале времени
Диск вращается с угловой скоростью, зависимость от времени которой задается графиком. Найти максимальный угол поворота диска (в радианах) в интервале времени  .
.
4.9  Диск вращается с угловым ускорением, зависимость от времени которого задается графиком. Найти угловую скорость диска в момент времени
Диск вращается с угловым ускорением, зависимость от времени которого задается графиком. Найти угловую скорость диска в момент времени 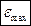 .
.
5.1 Частица движется в плоскости так, что ее импульс зависит от времени по закону а) 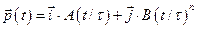 . Найти модуль силы, действующей на частицу
. Найти модуль силы, действующей на частицу 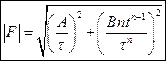 .
.
5.2 Частица движется в плоскости так, что ее импульс зависит от времени по закону а) 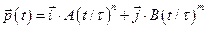 . Найти тангенс между осью x и вектором силы, действующей на частицу
. Найти тангенс между осью x и вектором силы, действующей на частицу  .
.
5.3 Частица движется в плоскости так, что ее импульс зависит от времени по закону а)  . Найти тангенс между осью y и вектором силы, действующей на частицу
. Найти тангенс между осью y и вектором силы, действующей на частицу  .
.
5.4 Частица массы m=1 движется в плоскости так, что ее импульс зависит от времени по закону а) 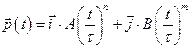 . Найти ускорение частицы
. Найти ускорение частицы 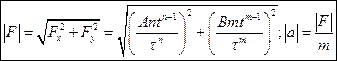 .
.
5.5 Частица движется в плоскости под действием силы, которая зависит от времени по закону
а) 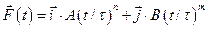 . Найти модуль изменения импульса за интервал времени
. Найти модуль изменения импульса за интервал времени  .
.
5.6 Небольшой шарик массы m летит со скоростью 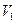 под углом
под углом 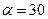 к горизонтальной плоскости. После неупругого удара он отскакивает со скоростью
к горизонтальной плоскости. После неупругого удара он отскакивает со скоростью 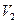 под углом
под углом  к плоскости. Время соударения
к плоскости. Время соударения 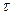 Найти а) Модуль средней силы трения шарика о плоскость; б) модуль средней силы нормальной реакции опоры, действовавшие во время удара. а)
Найти а) Модуль средней силы трения шарика о плоскость; б) модуль средней силы нормальной реакции опоры, действовавшие во время удара. а)  . б)
. б) 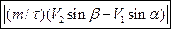 .
.
5.7 Небольшой шарик массы m летит со скоростью 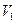 под углом
под углом 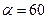 к горизонту и падает на вертикальную стену. После неупругого удара он отскакивает со скоростью
к горизонту и падает на вертикальную стену. После неупругого удара он отскакивает со скоростью 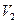 под углом
под углом 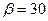 к горизонту. Время соударения
к горизонту. Время соударения 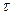 . Найти а) модуль средней силы трения шарика о стену, б) модуль средней силы нормальной реакции со стороны стены а)
. Найти а) модуль средней силы трения шарика о стену, б) модуль средней силы нормальной реакции со стороны стены а)  б)
б) 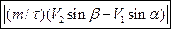 .
.
5.8 Частица с начальным импульсом  движется в плоскости под действием силы, которая зависит от времени по закону а)
движется в плоскости под действием силы, которая зависит от времени по закону а) 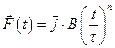 . Найти модуль импульса.
. Найти модуль импульса. 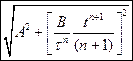 .
.
6.1 Тонкий однородный стержень массы m и длины L может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец. В оси действует момент сил трения 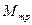 .Стержень приводят в горизонтальное положение и отпускают без толчка. Найдите угловое ускорение в начальный момент времени.
.Стержень приводят в горизонтальное положение и отпускают без толчка. Найдите угловое ускорение в начальный момент времени.  .
.
6.2 Тонкий однородный стержень массы m и длины L может вращаться в вертикальной плоскости без трения вокруг горизонтальной оси проходящей через его конец. Стержень располагают а) под углом  к горизонту; б) под углом
к горизонту; б) под углом  к вертикали и отпускают без толчка. Найдите его угловое ускорение в начальный момент времени. а)
к вертикали и отпускают без толчка. Найдите его угловое ускорение в начальный момент времени. а)  . б)
. б) 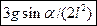 .
.
6.3 Тонкий однородный стержень массы m и длины L может вращаться в горизонтальной плоскости без трения вокруг вертикальной оси С, проходящей через середину стержня. К концу стержня в плоскости вращения под углом  к стержню прикладывают силу F. Найдите угловое ускорение стержня в начальный момент времени.
к стержню прикладывают силу F. Найдите угловое ускорение стержня в начальный момент времени. 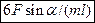 .
.
6.4 Тонкий однородный стержень массы m и длины L может вращаться в горизонтальной плоскости без трения вокруг вертикальной оси С, проходящей через середину стержня. В оси действует момент силы трения 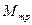 . К концу стержня в плоскости вращения перпендикулярно стержню прикладывают силу F. Найдите угловое ускорение стержня в начальный момент времени.
. К концу стержня в плоскости вращения перпендикулярно стержню прикладывают силу F. Найдите угловое ускорение стержня в начальный момент времени.  .
.
6.5 Тонкая однородная пластина в виде квадрата со стороной b может вращаться без трения в вертикальной плоскости вокруг горизонтальной оси, проходящей через центр масс C. Момент инерции пластины относительно оси C равен I. К середине стороны квадрата приклеили маленький грузик массой m и отпустили без толчка. Найдите угловое ускорение получившийся фигуры в начальный момент времени. 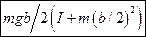 .
.
6.6 Тонкая однородная прямоугольная пластина со сторонами b и a может вращаться без трения в вертикальной плоскости вокруг горизонтальной оси, проходящей через центр масс C. Момент инерции пластины относительно оси C равен I. К середине стороны пластины приклеили маленький грузик массой m и отпустили без толчка. В начальный момент сторона пластины была вертикальна. Найдите угловое ускорение получившийся фигуры в начальный момент времени. 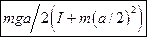 .
.
6.7 Тонкий однородный стержень длины L может вращаться в гориз. пл-сти вокруг вертикальной оси, проходящей ч/з середину стержня. К концу стержня приложена сила 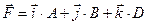 . Чему равна проекция момента силы на ось z.
. Чему равна проекция момента силы на ось z. 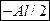 .
.
6.8 Маленький шарик поместили в точку с радиусом- вектором 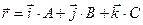 . В некоторый момент на шарик подействовали силы а)
. В некоторый момент на шарик подействовали силы а)  б)
б)  в)
в)  . Найти модуль момента силы относительно начала отсчета. а)
. Найти модуль момента силы относительно начала отсчета. а) 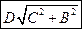 б)
б) 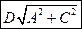 в)
в) 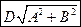 .
.
6.9 Маленький шарик поместили в точку с радиусом- вектором 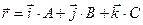 . В некоторый момент на шарик подействовали силой
. В некоторый момент на шарик подействовали силой 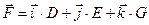 . Найти проекцию момента силы относительно начала координат а) на ось x б) на ось y в) на ось z а)
. Найти проекцию момента силы относительно начала координат а) на ось x б) на ось y в) на ось z а)  б)
б) 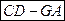 в)
в) 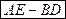 .
.
|
|
|
|
|
Дата добавления: 2014-12-25; Просмотров: 4421; Нарушение авторских прав?; Мы поможем в написании вашей работы!