Поправка компаса и способы ее определения 3 страница

p = ab = 1.

На картах, составленных в равновеликих проекциях, можно измерять площади и сопоставлять их. Свойство равновеликости сохраняется независимо от размеров картографируемых участков. Поэтому измерения можно производить и на больших площадях.

Равнопромежуточные проекции. Равнопромежуточными называются проекции, сохраняющие постоянство масштаба по одному из главных направлений. Вследствие этого бесконечно малый круг поверхности глобуса изобразится на плоскости проекции эллипсом, у которого одна из осей, сохранив величину, останется равной радиусу этого круга. Таким образом, основное условие равнопромежуточных проекций выражается так:

а=1 или b= 1;
р = а или р = b.

Искажение углов и площадей в равнопромежуточной проекции выражается формулами:

sin ω = (a - 1): (a + 1);
v_p = a - 1.

где v_р — увеличение масштаба площадей.

Произвольные проекции. Проекции, не относящиеся ни к одной из рассмотренных групп, но обладающие какими-либо другими, важными для практики свойствами, называются произвольными.
К числу наиболее часто используемых, произвольных проекций можно отнести центральную перспективную проекцию, на которой дуги больших кругов изображаются прямыми линиями.

По виду меридианов и параллелей нормальной картографической сетки проекции делятся на следующие основные группы:
— конические;
— азимутальные;
— цилиндрические;
— произвольные.

Из всех перечисленных здесь рассматриваются лишь те виды проекций, которые используются или могут использоваться для построения морских карт.

Конические проекции. Коническими называются проекции, у которых меридианы нормальной сетки изображаются прямыми, сходящимися в общей точке под углами, пропорциональными разности долгот, а параллели нормальной сетки изображаются концентрическими окружностями, имеющими общий центр в точке пересечения меридианов (рисунок). Конические проекции определяются уравнениями:

λ = α λ_o
ρ = f (φ) (74)

где λ — разность долгот на проекции;
α — коэффициент пропорциональности (обычно меньше единицы), называемый показателем конической проекции;
λ_о — угол между меридианами в натуре;
ρ — радиус параллели сетки.

Название конических такие проекции получили оттого, что они могут быть получены не только аналитически, но и путем геометрического проектирования поверхности глобуса на поверхность касательного или секущего глобус конуса, ось которого совпадает с географической осью глобуса. Проектирование при этом осуществляется из точки зрения, находящейся на оси конуса. На параллели, по которой поверхность конуса касается глобуса (а также на параллелях сечения глобуса конусом), масштаб равен единице. С удалением от параллели касания в обе стороны масштаб возрастает. При проектировании на секущий конус масштаб между параллелями сечения будет меньше масштаба глобуса. т. е. меньше главного масштаба.

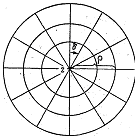
Азимутальные проекции. Азимутальными называются проекции, у которых меридианы нормальной сетки изображаются прямыми линиями, исходящими из общего центра, под углами, равными соответствующим углам между меридианами на глобусе, а параллели имеют вид концентрических окружностей с центром в точке схождения меридианов (рисунок-круг). Уравнения меридианов и параллелей нормальной сетки в азимутальных проекциях имеют вид

δ = λ_o
ρ = f (φ) (75)

где δ —угол между меридианами нормальной сетки;
λ_o — угол между меридианами на глобусе;
ρ —-радиус параллели.нормальной сетки.

Из приведенного, определения видно, что азимутальные проекции являются частным случаем конических проекций, когда α =1. Точка схождения меридианов в азимутальных проекциях является изображением полюса нормальной системы координат. Вид функции ρ = f (φ) определяет свойства азимутальных проекций (равноугольность, равновеликость или равнопромежуточность).
К классу азимутальных, проекций относятся перспективные проекции, получающиеся путем проектирования точек поверхности глобуса (шара) на картинную плоскость лучами, исходящими из постоянной точки. Эта точка называется точкой зрения. Картинная плоскость может или касаться поверхности проектируемого глобуса, или находиться от него на некотором удалении, или пересекать ее. Точка зрения выбирается на перпендикуляре к картинной плоскости, проходящем через центр проектируемого глобуса.

В зависимости от расположения точки зрения относительно центра глобуса перспективные проекции делятся:
— на ортографические, когда точка зрения удалена в бесконечность;
— на внешние, когда точка зрения находится на конечном расстоянии от центра проектируемого глобуса, но далее точки, представляющей антипод полюса нормальной системы координат;
— на стереографические, когда расстояние от центра глобуса до точки зрения равно радиусу глобуса, т. е. когда точка зрения помещается в точке шара, противоположной полюсу нормальной системы координат (в точке — антиподе полюса нормальной системы координат);
— на центральные (гномонические), когда точка зрения помещена в центре глобуса.

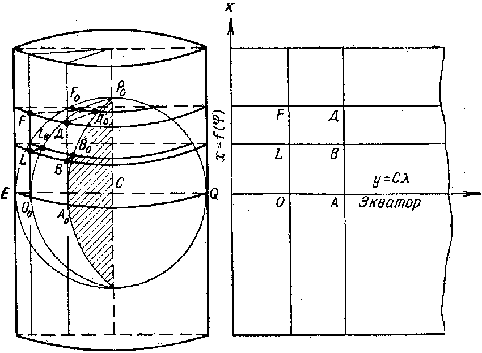
Цилиндрические проекции. Цилиндрическими проекциями называются такие, параллели и меридианы нормальной сетки которых изображаются взаимно перпендикулярными прямыми. Удаление параллелей сетки от экватора является функцией широты, расстояния между меридианами пропорциональны разностям долгот.
Общие уравнения цилиндрических проекций имеют вид

x = f (φ)
y = C λ (76)

Вид функции x = f (φ) и коэффициент С определяют важнейшие свойства цилиндрической проекции. Изменяя их, можно получить равноугольную, равнопромежуточную, равновеликую или произвольную проекцию. Цилиндрические проекции могут быть получены путем проектирования поверхности глобуса на касательный или секущий глобус цилиндр (рисунок). При проектировании на касательный по экватору цилиндр масштаб вдоль экватора сохраняет равенство главному масштабу, т. е. экватор глобуса изображается на проекции без искажений. При проектировании на секущий цилиндр ли-ниями нулевых искажений будут являться параллели сечения.

Из цилиндрических наиболее употребительны в кораблевождении прямая и поперечная проекции Меркатора и поперечная проекция Гаусса.

§ 24. Понятие об изображении земного эллипсоида на шаре

Применительно к сфероидической поверхности Земли ее плоское изображение, т. е. картографическую проекцию, можно получить, если непосредственно выразить координаты любой точки на плоскости через географические координаты этой точки на поверхности эллипсоида. Такой прямой путь изображения земного эллипсоида на плоскости применяется обычно для получения нормальных картографических сеток, когда можно сравнительно просто выразить плоские прямоугольные (или полярные) координаты изображаемой точки в функции ее географических координат.
При построении поперечных и косых картографических сеток математическое выражение связи между картографическими и географическими координатами изображаемой точки может оказаться чрезвычайно сложным. В этих случаях построение картографической проекции может быть выполнено следующим образом: предварительно земной эллипсоид изображается на шаре, а затем сферическая поверхность переносится на плоскость на основе уже менее сложного выражения плоских координат в функции сферических географических координат.

Проекции, которые получаются путем предварительного изображения сфероида на шаре, а затем проектирования шара на плоскость, называются двойными проекциями. Проектирование эллипсоида на шар может быть произведено с соблюдением любого заданного условия: равноугольности, равнопромежуточности или равновеликости.
Свойства изображения эллипсоида на шаре и характер получающихся при этом искажений определяются видом зависимости сферических координат φ ' и λ ' от сфероидических географических координат φ и λ, т. е. видом функций

φ ' = f (φ)
λ ' = α λ

где α — некоторый постоянный коэффициент.

При изображении всей поверхности земного эллипсоида на шаре получающиеся искажения в некоторых частях шара могут оказаться больше допустимых величин. Тогда в целях уменьшения искажений изображение поверхности земного эллипсоида на шаре осуществляется лишь в пределах некоторого широтного пояса, в котором расположен участок, подлежащий картографированию,

Глава 4

ЦИЛИНДРИЧЕСКИЕ ПРОЕКЦИИ, ПРИМЕНЯЕМЫЕ ДЛЯ ПОСТРОЕНИЯ МОРСКИХ НАВИГАЦИОННЫХ КАРТ

§ 25. Основные требования, предъявляемые к морской навигационной карте

Выбор картографической проекции при построении карты определяется теми целями и задачами, для решения которых карта предназначена. Соответственно этим задачам, их характеру и особенностям к картографической проекции и содержанию карты предъявляются определенные требования. К проекциям, используемым для построения морских навигационных карт, предъявляются следующие основные требования.

1. Проекция должна обладать свойством равноугольности (конформности). В практике кораблевождения штурман постоянно производит измерения направлений (пеленгов) и углов между ориентирами на земной поверхности, которые затем прокладываются на карте. Равноугольность проекции карты облегчает и обеспечивает наибольшие удобства и быстроту прокладки результатов таких измерений. Кроме того, равноугольность проекции в наибольшей степени способствует опознанию обстановки на местности по ее изображению на карте, и наоборот.

2. Траектория движения корабля, идущего неизменным курсом, и, следовательно, составляющая с земными меридианами постоянный угол, на морской карте должна изображаться прямой линией, как наиболее простой для Графической ее прокладки. Такая линия называется локсодромией. Если локсодромия будет изображаться на проекции прямой линией, сохраняющей постоянными углы пересечения с меридианами, значит, меридианы должны быть параллельными прямыми. Но параллели и меридианы всегда перпендикулярны друг другу. Следовательно, картографическая сетка морской карты, удовлетворяющая первому и второму условиям, должна состоять из двух семейств прямых линий — географических меридианов и параллелей, взаимно перпендикулярных друг другу.

3. Поскольку в практике кораблевождения решение ряда навигационных задач производится при условии принятия фигуры Земли за шар, было бы практически удобно, чтобы на картографической сетке морской карты дуга большого круга — ортодромия изображалась также наиболее простой линией—прямой или близкой к прямой линией. Это требование особенно важно для обеспечения плавания в высоких широтах.

4. Наконец, одним из важных требований, предъявляемых к картографической проекции, является требование давать высокую точность изображения по всей картографируемой площади. Иначе говоря, это требование состоит в том, чтобы искажения длин как в разных местах картографируемой площади, так и около одной точки по разным направлениям не превышали ошибок графических измерений и построений на карте с помощью прокладочного штурманского инструмента.

Удовлетворить одновременно всем перечисленным требованиям ни одна картографическая проекция не может. Поэтому для целей кораблевождения строятся и издаются карты в разных проекциях, а используются при решении отдельных задач те из них, которые в данных конкретных условиях наилучшим образом отвечают перечисленным требованиям и требованиям решаемой задачи.

Основными проекциями, используемыми для составления морских карт, являются:

— равноугольная цилиндрическая проекция Меркатора;
— равноугольная поперечная цилиндрическая проекция Гаусса;
— равноугольная азимутальная, (стереографическая) проекция;
— центральная (гномоническая) проекция;
— равноугольная поперечная проекция Меркатора.

§ 26. Общие формулы цилиндрических проекций

Уравнения меридианов и параллелей цилиндрических проекций в общем виде определяются выражениями (76);
x = f (φ);
y = C(λ)
где С—коэффициент пропорциональности, определяющий расстояния между меридианами.
Отдельные цилиндрические проекции различаются между собой лишь видом функции f (φ).

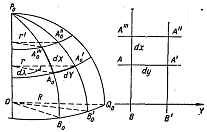
Так как меридианы и параллели на проекции и в натуре взаимно перпендикулярны, их направления являются главными направлениями. Следовательно, масштабы вдоль меридианов и параллелей имеют экстремальные значения, а именно: m = а и n = b. Бесконечно малая трапеция A₀A'₀A''₀A'''₀ (рисунок), образованная на поверхности шара (или эллипсоида) пересечением бесконечно близких друг к другу меридианов и параллелей, на плоскости проекции изобразится прямоугольником АА'А"А"' со сторонами dx и dy. Отрезок A₀A'''₀ представляет собой бесконечно малую часть меридиана — Rdφ — на шаре или Mdφ — на эллипсоиде, а отрезок A₀A'₀ — бесконечно малую часть параллели — rdλ = Rcosφ —на шаре или rdλ = Ncosφdλ — на эллипсоиде, где r —радиус параллели в широте φ, равный Rcosφ для шара и Ncosφ для эллипсоида.

На основании определения масштаба, выразим масштабы по меридиану m и параллели n:

для шара
m = dx / Rdφ n = dy / rdλ = dy / R cosφ dλ (77)

для эллипсоида
m = dx / Mdφ n = dy / rdλ = dy / N cosφ dλ (78)

Наибольшее искажение направлений выражается формулой (65). Чтобы воспользоваться этой формулой, нужно знать полуоси а и b эллипса искажений. Но так как в цилиндрических проекциях главные направления совпадают с меридианами и параллелями, то полуосям а и b соответствуют экстремальные масштабы m и n, поэтому

sin ω = (a - b) / (a + b) = (m - n) / (m + n) (79)

Таким образом, общими формулами для всех цилиндрических проекций будут:

Для эллипсоида: x = f (φ) y = Cλ m = dx / Mdφ n = dy / Ncosφdλ sin ω = (a - b) / (a + b) = (m - n) / (m + n)

Для шара: x = f (φ) y = Cλ m = dx / Rdφ n = dy / Rcosφdλ sin ω = (a - b) / (a + b) = (m - n) / (m + n)

§ 27. Равноугольная цилиндрическая проекция Меркатора

Проекция, предложенная в 1569 г. голландским картографом Герардом Кремером, носившим, кроме того, латинское имя Меркатор, получила название проекции Меркатора. Эта проекция удовлетворяет двум основным требованиям, предъявляемым к проекциям для морских навигационных карт:
- она равноугольна;
- локсодромия на проекции изображается прямой линией.

Первое свойство проекции Меркатора — равноугольность выражается равенством масштабов по всем направлениям, т. е. а = b = m = n. Вследствие этого бесконечно малый кружок на поверхности Земли на карте в проекции Меркатора изобразится также бесконечно малым кружком.

Второе свойство определило вид географических меридианов и параллелей проекции: они представляют собой два семейства взаимно перпендикулярных прямых линий.
Нормальной картографической сеткой проекции Меркатора является сетка географических меридианов и параллелей, а нормальной системой сферических координат — географические координаты φ и λ.
Продифференцировав формулу (76) y =Сλ и подставив полученное значение dy в одну из формул (78) для цилиндрических проекций, получим

n = Cdλ / Ncosφdλ = C / Ncosφ - для эллипсоида и
n = Cdλ / Rcosφdλ = C / Rcosφ - для шара.

Для установления закона построения картографической сетки проекции Меркатора необходимо установить вид функции х = f(φ) в формулах (76).
Подставив значения m и n для эллипсоида из исходных формул (78) и приравняв их, можно написать

m = n = dx / Mdφ = C / Ncosφ

Из этого равенства имеем dx = C (M / N) * (dφ / cosφ).
Подставив значение радиусов кривизны М и N главных нормальных сечений земного эллипсоида из формул (6) и (7), получим

dx = C * {a * (1 - e²)(1 - e²sin² φ)½) / (1 - e²sin² φ)^3/2 *a} * dφ / cos φ,

откуда

dx = C * {(1-e²) / (1 - e²sin²φ)} * (dφ / cosφ)

Для интегрирования полученного выражения умножим в числителе e² на единицу, написав ее в виде sin²φ + cos²φ = 1, тогда

dx = C * {1 - (e²sin²φ + e²cos²φ) / (1 - e²sin²φ} * (dφ / cos φ} = C * {(1 - e²sin²φ - e²cos²) / (1 - e²sin²)} * dφ / cos φ = C * {(1 - e²sin²φ) / (1 - e²sin²φ) - (e²cos²φ) / (1 - e²sin²φ)} * (dφ / cos φ = C * (dφ / cos *φ) - C * {(e²cos²φ) / (1 - e²sin²φ) * dφ.

Сделаем подстановку, введя вспомогательную величину esinφ = sin ψ и ее дифференциал ecos φ dφ = cos ψdψ:

dx = C * (dφ / cosφ) - Ce{(cos ψ dψ)/(1 - sin²ψ)}.

Подставляя в последнее выражение 1 - sin²ψ = cos²ψ, получим

dx = C * {(dφ) / (cos φ)} - Ce{dψ) / (cos ψ)}.

Интегрирование последнего выражения дает:

x = C ln tg (45° + φ / 2) - Ce ln tg (45° + ψ /2).

Переписав полученное значение х в виде

x = C ln {tg(45° + φ / 2) / tg^e (45° + ψ / 2)}

и обозначив {tg(45° + φ / 2) / tg^e (45° + ψ / 2)} = U получим для х окончательное выражение

x = C ln U (80)

Таким образом, выявлен вид функции х = f (φ) для равноугольной цилиндрической проекции Меркатора.
Для завершения преобразований перейдем к аргументу φ, помня, что ранее была введена замена esin φ = sin ψ.

Так как

tg (45° + ψ / 2) = √ {(1 + sin ψ / (1 - sin ψ)} = √ {(1 + esinφ) / (1 - esin φ)},

то

tg^e (45° + ψ / 2) = {(1 + esin φ) / (1 - esin φ)}^e/2

Теперь полный вид искомой функции будет

x = C ln tg (45° + φ / 2){(1 - esin φ) / (1 + esin φ)}^e/2 (81)

Для определения значения постоянной С поставим дополнительное условие: пусть масштаб на экваторе равен единице: n_о = 1. Это условие определяет положение цилиндра, на который проектируется земной эллипсоид: он касается его по экватору и, следовательно, на экваторе масштаб (n_о) равен единице, а искажения отсутствуют. Положив, таким образом, по условию n_o = 1 и φ = 0, из выражения

m = n_o = 1 = C / Ncosφ 1 = C / N С=N. Но на экваторе N = а, следовательно, С=а.

Теперь найденная функция примет вид

x = a ln U (82)

Формула (82) определяет удаление параллели с широтой φ от экватора, выраженное в единицах длины, принятых для измерения большой полуоси земного эллипсоида а. Выведенная величина х измеряется вдоль меридиана, а потому ее принято называть меридиональной частью и обозначать буквой D. Если в уравнении (82) выразить а в экваториальных минутах, то формула меридиональной части примет вид:

D = a_{экв.мин} ln U (83)

Меридиональной частью (D) называется расстояние на проекции Меркатора по меридиану от экватора до данной параллели, выраженное в экваториальных минутах при масштабе на экваторе, равном единице. Значение и область применения меридиональных частей в картографии и в кораблевождении велики, так как в противоположность переменным численным значениям длины одной минуты меридиана земного эллипсоида меридиональные части выражаются в постоянных величинах, равных длине минуты экватора p_э применяемого эллипсоида. Для референц-эллипсоида Красовского р_э = а arc 1' = 1855,356 м. Постоянство единицы меридиональных частей представляет известное удобство при различных вычислениях.
В Картографических таблицах (1), а также в Мореходных таблицах МТ (табл. 26) приводятся меридиональные части для широт от 0 до 89°59'. В практике удобнее пользоваться формулой, где меридиональная часть выражена через экваториальные минуты и десятичные, а не натуральные логарифмы.
Поэтому с учетом того, что а = 1 / arc 1' = 3437,7468 и Моd= 0,434294, формулы (80) и (81) перепишем в следующем виде:

D = 7915',70447 lg tg (45° + φ / 2){(1 - esin φ) / (1 + esin φ)}<="" sup="">; (84)
D = x = 7915',70447 lg U. (85)

Для Земли—шара (е=0, а=R) уравнения меридианов и параллелей в проекции Меркатора имеют вид

x = D = R ln tg (45° + φ / 2)
y = Rλ (86)

Таким образом, для равноугольной цилиндрической проекции Меркатора получены формулы:

Для сфероида: x = a ln tg (45° + φ / 2){(1 - esin φ) / (1 + esin φ)}^e/2; y = aλ m = n = (a / N)sec φ ω = 0.

Для шара: x = R ln tg (45° + φ / 2); y = Rλ m = n = sec φ ω = 0.

При построении карты в проекции Меркатора всегда указывается параллель, к которой отнесен главный масштаб. Эта параллель называется главной параллелью. Главные параллели установлены для отдельных морей и океанов, их перечень приведен в Картографических таблицах.
§ 28. Локсодромия

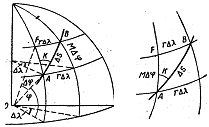
Траектория корабля, идущего неизменным курсом, представляет собой на Земной поверхности линию двоякой кривизны, пересекающую все меридианы под одним и тем же углом. Такая кривая называется локсодромией, что в переводе с греческого означает «косой бег» (рисунок). Локсодромия на поверхности Земли спиралеобразно приближается к полюсу, но никогда его не достигает.

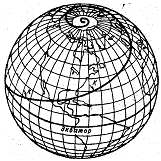
Для вывода уравнения локсодромии рассмотрим элементарный треугольник АВF на земном эллипсоиде, образованный отрезками меридиана АF, параллели FB и локсодромии AF, составляющей с меридианами одинаковые углы К. По малости сторон треугольник АВF можно принять за плоский и тогда

tg K = rΔλ / MΔφ = NcosφΔλ / MΔφ.

Подставив в полученную формулу значения M и N, из формул (6) и (7), получим

tg K = {a(1 - e²sin²φ)^3/2cosφΔλ / (1 - e²sin²φ)½ * a(1 - e²)Δφ} = {(1 - e²sin²) / (1 - e²)} * cos φ (Δλ / Δφ.

Переходя от элементарно малых величин Δφ и Δλ к их дифференциалам, последнее выражение перепишем в виде

dλ = tg K {(1 - e²) / (1 - e²sin²φ)} * (dφ / cos φ).

Заменив в числителе 1 - e² на 1 - e²(sin² + cos²φ), получим

dλ = tg K [ (1 - e²sin²φ) / (1 - e²sin²φ - e * { (ecos²φ) / (1 - e²sin²φ)} ] * (dφ / cos φ,

откуда

dλ = tg K { (dφ / cos φ) - e * { (ecos φ dφ) / (1 - e²sin²φ) }.

Интегрирование последнего выражения в пределах от A (φ₁, λ₁) до B (φ₂, λ₂) дает

λ₂ - λ₁ = {tg K ∫^φ_2φ1 dφ / cos φ} - e * tg K ∫^φ_2φ1 cos φ dφ / (1 - e²sin²φ

Произведя необходимые преобразования подынтегрального ∫^φ_2φ1 cos φ dφ / (1 - e²sin²φ) выражения, как показано в предыдущем параграфе, получим уравнение локсодромии АВ на карте проекции Меркатора с учетом сжатия Земли

λ₂ - λ₁ = tg K [ ln tg (45° + φ₂) - ln tg (45° + φ₁ / 2) ] - e tg K [ln tg (45° + ψ₂ / 2) - ln tg (45° + ψ₁),]
окончательный вид которого будет

λ₂ - λ₁ = tg K [ ln tg (45° + φ₂ / 2){(1 - esin φ₂) / (1 + e sin φ₂)^e/2 - ln tg (45° + φ₁ / 2) * { (- esin φ₁ / (1 + e sin φ₁)^e/2]

где φ₁, λ₁, φ₂, λ₂ — координаты точек, через которые проходит локсодромия.

Без учета сжатия Земли уравнение локсодромии имеет вид

λ₂ - λ₁ = tg K [ ln tg (45° + φ₂ / 2) - ln tg (45° + φ₁ / 2) ] (88)

Выражения, стоящие в квадратных скобках уравнений (87) и (88), представляют собой разности меридиональных частей: D₂ —для параллели с широтой φ₂ и D₁ — для параллели с широтой φ₁.
Поэтому выражения (87) и (88) могут быть представлены в виде
λ₂ - λ₁ = tg K (D₂ - D₁). (89)

Последнее уравнение показывает, что локсодромия на проекции Меркатора изображается прямой линией. Иначе и быть не может, так как систему параллельных между собой прямых (меридианов) под одним углом пересекает только прямая линия. Приняв одну из точек, через которые проходит локсодромия, на экваторе, т. е. считая φ₁ = 0 и λ₁ = λ_o, а координаты произвольной точки В текущими, т.е. φ₂ = φ и λ₂ = λ, перепишем уравнение локсодромии в следующем виде (формулы 90):

— с учетом сжатия Земли:

λ = tg K [ ln tg (45° + φ / 2) * { (1 - e sin φ) / (1 + e sin φ) }^e/2} ] + λ_o

— без учета сжатия Земли:

λ = tg K (45° + φ / 2) + λ_o

Выведенные уравнения позволяют по известным курсу К, долготе точки пересечения экватора λ_о и одной из текущих координат локсодромии вычислить вторую координату. Исследуем полученные уравнения с целью выявления свойств локсодромии.

1. Положив в формуле (87) или (88) K = 0° или K = 180°, найдем, что λ₂ - λ₁ = 0 или λ₂ = λ₁, т. е. λ = const. В этом случае локсодромия совпадает с меридианом и проходит через точки обоих полюсов.

2. При K = 90° или K = 270° tg K = ∞. Но так как разность долгот точек локсодромии λ₂ - λ₁ величина конечная, то один из членов формулы (87) или (88) дол-жен быть равен нулю, т. е. ln tg (45° + φ₂ / 2) - ln tg (45° + φ₁ / 2) = 0,
следовательно,
φ₂ = φ₁, то есть φ = const.

Локсодромия в этих случаях совмещается с параллелью или с экватором (при φ = 0°).

3. Уравнение (90) приведем к такому виду:
tg (45° + φ / 2) = e_{(λ - λo)ctg K} (91)

Полученное уравнение показывает, что каждому значению широты φ соответствует только одно значение долготы λ, т. е. локсодромия пересекает каждую параллель только один раз. Придавая долготе значения λ, λ + 2π, λ + 4π, λ + 6π и т. д., будем получать каждый раз все новые возрастающие значения широты. Это означает, что локсодромия пересекает каждый меридиан бесчисленное множество раз, стремясь к полюсу и не достигая его. Исключение составляют лишь случаи, когда K =0° и K = 180°.

§ 29. Изменение масштаба на карте в проекции Меркатора

Расстояние по меридиану между двумя параллелями на проекции Меркатора определяется разностью меридиональных частей этих параллелей:

D₂ - D₁ = РМЧ (92)

Длина одной минуты дуги меридиана на данной параллели карты в проекции Меркатора, выраженная в миллиметрах, носит название меркаторской мили. Величиной меркаторской мили, графически изображенной на боковых (восточной и западной) рамках карты, пользуются как единицей линейного масштаба для измерения расстояний при работе на карте.
Численное значение меркаторской мили Θ (мм) на данной параллели φ, знаменатель частного масштаба на которой равен С, может быть вычислено по формуле
Θ = Δ 1' / C (93)

Дата добавления: 2014-12-25