Вычисление размеров рамки карты

Решение.

Пример.

Последовательность действий при вычислении картографической сетки легко уясняется из решения следующего примера.

Рассчитать картографическую сетку проекции Меркатора для карты, охватывающей район с границами:

js = 59°00,0'N; lw = 25°00,0'Ost; jN = 60° 15,0'N; lost = 28°20,0'Ost в масштабе mo = 1:200000 по главной параллели jо=60°. Меридианы сетки провести через 30'.

1. Расчет е и выбор Δl.

Из табл. 4 Картографических таблиц по jо =60°N и масштабу mo =1:200000 выбираем е = 4,6501 мм. При невозможности воспользоваться Картографическими таблицами единица карты рассчитывается с применением таблиц логарифмов по формуле e = Po / Co Po = 930015; lg Ро = 5,96849 Со = 200000; lg Со = 5,30103, lg е = 0,66746, е = 4,6501 мм.

Промежуток практически постоянного масштаба, т. е. широтный интервал между параллелями, выбирается из табл. 6 Картографических таблиц. В нашем примере он равен 13,1'. Округляя его в меньшую сторону, примем Δj =10'.

jN = 60°15,0' N, DN = 4537,471', lg (DN - DS) = 2,17052,

js = 59°00,0', DS = 4389,384', lg е = 0,66746, DN - DS = 148,087', lg b = 2,83798, b = 688,6 мм,

lw = 25°00,0' Ost, lg (lo - lw) = 2,30103, lo = 28°20,0' Ost, lg е = 0,66746,

lo - lw = 200', lg а = 2,96849, a = 930 мм.

§ 31. Поперечная цилиндрическая равноугольная проекция Гаусса

При выполнении некоторых специальных навигационных задач проекция Меркатора, имеющая основными координатными линиями меридианы и параллели, оказывается недостаточно удобной. Так, например, чтобы вычислить географические координаты какой-либо точки для нанесения ее на карту, приходится прибегать к трудоемким и сложным формулам, затрачивая на вычисление много времени. Значительно проще такого рода задачи решаются с использованием прямоугольных координат вместо географических. Замена географических координат прямоугольными позволяет производить расчеты по несложным формулам плоской тригонометрии. Непрерывное изменение масштаба на карте в проекции Меркатора также представляет известное неудобство, так как пределы полосы с практически постоянным масштабом весьма ограничены. На практике нередко бывает удобнее иметь карту с незначительными искажениями длин и площадей, а также с масштабом, который можно практически принимать постоянным в пределах всего листа карты. Так, при выполнении ряда работ, требующих высокой точности, целесообразно применять проекцию, на плоскости которой изображение строится как план, где измеренные углы и расстояния переносятся на планшет без исправления поправками за искажение проекции. Для обеспечения этого требования проекция должна иметь малые искажения длин, не превышающие ошибок графических построений на планшете (0,2 мм). Измеренным на местности сферическим углам должны соответствовать на карте плоские углы с ничтожно малыми их искажениями.
Таким образом, основным требованием, предъявляемым к проекции, используемой для составления топографических карг, различных планшетов и для обработки триангуляции, является небольшая величина искажений углов и длин и простота их учета. Такой проекцией является картографическая проекция, предложенная в начале XIX в. известным немецким ученым Гауссом. Проекция Гаусса по свойству изображения является равноугольной, а по способу построения картографической сетки — поперечной цилиндрической проекцией эллипсоида. Принципиально проекция/Гаусса может быть также получена путем проектирования шара, представляющего равноугольную проекцию эллипсоида, на боковую поверхность касательного цилиндра, ось которого лежит в плоскости экватора.
Нормальной системой координат проекции Гаусса, является система сферических (сфероидических) прямоугольных координат X, У, экватором которой служит средний меридиан картографируемой зоны, а начальным меридианом — земной экватор.
Средний меридиан, выполняющий роль экватора нормальной системы координат проекции Гаусса, называется осевым меридианом. Картографическая проекция Гаусса постановлением Геодезического комитета Госплана СССР в 1928 г. принята основной для выполнения топографических и триангуляционных работ. Этим же постановлением для всей территории СССР введена единая система прямоугольных координат.

§ 32. Сферические прямоугольные координаты

В отличие от географических сферические координаты являются поверхностными координатами, представляющими собой дуги больших кругов, и выражаются в линейной мере — в километрах или в метрах. За начало счета сферических прямоугольных координат принимается точка пересечения экватора с одним из меридианов, называемым осевым.
Выберем на экваторе произвольную точку О (рисунок) с долготой Lо и обозначим точки экватора с долготами L ± 90° через Е и Q. Через выбранную точку О и заданную на сфере точку Aо проведем их меридианы. Через точку Ао проведем дугу большого круга, плоскость которого составит с плоскостью меридиана PNOPS угол, равный 90°. Если теперь точку О принять за начало системы координат и координатными осями считать: осевой меридиан PNOPS —осью абсцисс, а экватор EOQ — осью ординат, то положение точки Аo может быть определено сферической абсциссой ОВо = Х и сферической ординатой ВоАо =Y. Сферические абсциссы Х отсчитываются от экватора в линейной мере (километрах или метрах) и считаются положительными для точек, лежащих к северу от экватора, и отрицательными для точек, расположенных южнее экватора. Сферические ординаты Y определяют удаление точек от осевого меридиана по дугам больших кругов, проходящим через эти точки перпендикулярно осевому меридиану.

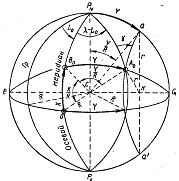
Ординаты Y также выражаются в линейной мере. Ординаты Y принимаются положительными для точек, лежащих восточнее осевого меридиана, и отрицательными для точек, расположенных к западу от осевого меридиана. Связь прямоугольных сферических Х и Y и географических j и l координат может быть выведена из треугольника ВоРNАо (рисунок). Применив к треугольнику теорему синусов, получаем
sin (Y / R) = cos j sin (l - Lo). (112)

По формуле тангенс катета прямоугольного сферического треугольника найдем

tg {90 - (X / R)} = tg (90 - j) cos (l - Lo)

или

ctg (X/R) = ctg j cos (l - Lo), (113)

где Y / R и X / R - дуги больших кругов - сферические прямоугольные координаты, выраженные в радианах;

X и Y - сферические прямоугольные координаты, выраженные в линейных единицах;

R - радиус Земли.

Геометрическое место точек, имеющих одинаковую ординату У, представляет собой малый круг аАоО.1 (рисунок вверху), плоскость которого параллельна плоскости осевого меридиана. Радиус такого малого круга зависит от величины сферической ординаты Y и определяется по формуле r = R cos (Y/R). (114)
Сферический угол PNAoa = g при заданной точке Aо между ее меридианом и малым кругом, плоскость которого параллельна плоскости осевого меридиана, называется углом схождения или сближения меридианов. Величина его зависит от разности долгот между осевым меридианом и меридианом точки Аo и от широты этой точки. Определяется угол сближения меридианов по формуле g = (l - Lo)sin j. (115)

Знак угла сближения меридианов определяется расположением точек относительно осевого меридиана. Для точек, расположенных восточнее осевого меридиана, угол сближения меридианов будет иметь знак плюс; для точек, находящихся западнее осевого
На плоскости проекции сферические прямоугольные координаты X, Y изображаются в виде плоских прямоугольных координат х, у. При этом на проекции образуется сетка, составленная двумя семействами взаимно перпендикулярных параллельных прямых линий. Сферический угол схождения меридианов g в силу равноугольности проекции изображается на проекции плоским углом схождения меридианов g в виде угла между меридианами и линиями y = сonst.

Дата добавления: 2014-12-25