Геометрический метод рассмотрения движения плоской фигуры в ее плоскости

Теорема Шаля 1: Всякое непоступательное перемещение плоской фигуры в ее плоскости из одного положения в другое может быть представлено как сумма двух перемещений: поступательного вместе с произвольной точкой, выбранной в качестве полюса, и вращательногоотносительно этого полюса. При этом поступательное перемещение зависит от выбора полюса, а вращательное от него не зависит.

Под вращательным перемещением плоской фигуры относительно полюса понимается вращательное перемещение этой плоской фигуры вместе с НМС, сечением которой является эта плоская фигура, относительно оси, проходящей через полюс перпендикулярно плоской фигуре (или плоскости П₀).

Доказательство: На рис. 1 изображены два положения плоской фигуры и отрезка ВD в моменты времени t₁ и t₂: соответственно В₁D₁ и В₂D₂.

Выберем в качестве полюса точку D. Отрезок В₁D₁ перемещаем поступательно (т.е. параллельно самому себе) в положение , а затем поворачиваем вокруг полюса на угол 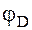. Точка попадет в точку В₂, так как длина отрезка ВD неизменна. Первая часть теоремы доказана.

Для доказательства второй части теоремы в качестве полюса выберем точку В. Отрезок В₁D₁ перемещаем поступательно (т.е. параллельно самому себе) в положение 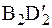, а затем поворачиваем вокруг полюса на угол 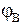. На рис. 1 видно, что поступательные составляющие перемещений отрезка ВD различны при выборе в качестве полюсов В и D (D₁D₂ В₁В₂), а вращательные составляющие равны, так как 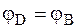, как накрестлежащие углы при двух параллельных и одной секущей.

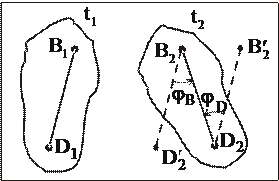
Рис. 2

Поскольку поступательная часть перемещения плоской фигуры с изменением полюса меняется, оказывается возможным выбрать полюс так, чтобы эта часть перемещения вообще отсутствовала.

Теорема Шаля 2: Всякое непоступательное перемещение плоской фигуры в ее плоскости из одного положения в другое может быть представлено как конечный поворот этой фигуры относительно определенного центра вращения.

Конечный поворот плоской фигуры относительно определенного центра вращения понимается в том же смысле, что и вращательное перемещение этой плоской фигуры в теореме Шаля 1.

Доказательство: На рис. 3 изображены два положения отрезка ВD в моменты времени t₁ и t₂: соответственно В₁D₁ и В₂D₂.

Соединим точки В₁ и D₁ соответственно с точками В₂ и D₂ и из середин отрезков В₁В₂ и D₁D₂ восстановим перпендикуляры. Точка пересечения этих перпендикуляров О — центр вращения (как будет доказано ниже).

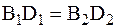, так как и 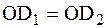, как наклонные, равноудаленные от перпендикуляра.

Из равенства треугольников следует, что .

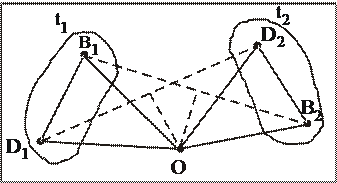
Рис. 3

После поворота на относительно точки О отрезок ОВ₁ совпадает с отрезком ОВ₂, одновременно ОD₁ отрезок должен совпасть с отрезком ОD₂, так как

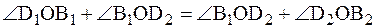, т. е.

,

и, как следствие, отрезок В₁D₁ совпадет с отрезком В₂D₂.

Таким образом, перемещение отрезка ВD из положения В₁D₁ в положение В₂D₂ представлено конечным поворотом относительно центра О.

Из доказанных теорем следует, что всякое непоступательное перемещение плоской фигуры в ее плоскости из одного положения в другое может быть представлено двумя способами: либо суммой поступательного и вращательного движений либо одним вращательным движением.

Дата добавления: 2014-12-25