Частотная модуляция. Спектр сигнала

До 1991 г., когда появились цифровые стандарты телефонии, частотная модуляция была универсальным методом передачи в любых сетях подвижной связи. Сейчас сети аналоговой сотовой связи практически исчезли, но продолжают работать транкинговые сети с ЧМ.

При ЧМ частота радиосигнала меняется прямо пропорционально мгновенному значению модулирующего напряжения [3], т.е. .

Соответственно, колебания радиочастоты

,

(3.19)

где f ₀ – центральная частота радиосигнала.

Максимальное отклонение частоты Δ f _max(t) называют девиацией частоты.

Речевые сигналы многочастотны. Более того, речь содержит наряду с отдельными дискретными составляющими шум, так что спектр речи сплошной. Поэтому – полигармонический сигнал. Для упрощения анализа ЧМ радиосигнала будем использовать моногармоническое модулирующее испытательное напряжение где Ω=2π F.

Тогда (3.19) можно преобразовать к виду

,

(3.20)

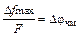где = kA – девиация частоты, – индекс частотной модуляции.

Иначе

.

(3.21)

Для проведения спектрального анализа ЧМ колебаний введем производящую функции Бесселя 1-го рода

.

(3.22)

где – функция Бесселя 1-го рода k -го порядка.

Подставляя (3.22) в (3.21), получаем

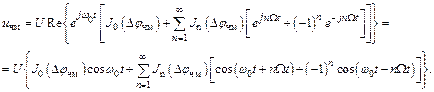
(3.23)

Таким образом, при модуляции гармоническим напряжением ЧМ сигнал имеет бесконечный линейчатый спектр (рис. 3.9), где амплитуды всех составляющих определяют функции Бесселя.

Рис. 3.9. Спектр ЧМ сигнала

Графики функций 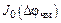… представлены на рис. 3.10.

Рис. 3.10. Графики функций Бесселя

Как следует из рис 3.10, амплитуда частоты f ₀ меняет знак, а при 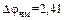и ряде последующих значений обращается в нуль. Максимумы функций расположены вблизи z = n. Чем больше , тем большее число составляющих будет значимым в спектре. Если , то спектр состоит из трех составляющих (рис. 3.11).

Рис. 3.11. Спектр ЧМ сигнала при малых индексах

Высокая помехозащищенность ЧМ сигналов достигается при . Поэтому в случае речевого модулирующего сигнала с полосой 300…3400 Гц, предварительно до модуляции вводят предкоррекцию сигнала, поднимая уровень его высокочастотных составляющих.

Теоретически полоса ЧМ сигнала бесконечна. Фактически сигнал ограничен полосой, включающей спектральные составляющие, содержащие не менее 90% полной мощности сигнала.

На практике полосу ЧМ сигнала часто определяют так [3]:

.

(3.24)

Теоретически ЧМ сигнал имеет постоянную амплитуду, однако из-за ограничения полосы возникает небольшая паразитная амплитудная модуляция. Поэтому при приеме ЧМ сигнал подвергают амплитудному ограничению, а при передаче в усилителях мощности используют слабоперенапряженные режимы работы транзисторов.

Дата добавления: 2014-12-26