Умножение дробных чисел в дополнительных кодах

. Возможны четыре случая знакосочетания сомножителей.

1) Мн>0,

Мт>0.

В этом случае дополнительный код сомножителей совпадает с прямым кодом и умножение выполняется по правилам умножения в прямых кодах, в результате чего получается верный результат.

2) Мн>0,

Мт<0.

Так как Мн и Мт имеют разные знаки, то результат будет иметь отрицательный знак. Следовательно, результат должен быть представлен в дополнительном коде [Мн∙Мт]_доп=2-Мн∙Мт. Для формирования произведения выполним умножение Мн на Мт¢ (дополнение):

Мн∙Мт¢= Мн ∙(1 - Мт)= Мн - Мн∙Мт.

Таким образом, погрешность Δ умножения равна разности [Мн∙Мт]_доп. и Мт∙Мн¢

Δ=2-Мн∙Мт- Мн + Мн∙Мт=2-Мн=[-Мн]_доп=[ [Мн]_доп]_доп

и должна быть внесена в полученный результат в качестве поправки.

Пример: Мн = 0,1011 (алгоритм умножения А)

Мт = - 0,1101

Δ= [- Мн]_доп = 1,0101

[- Мт]_доп = 1,0011

0,0000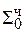

⁺ 0,1011 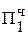= Мн b₄

0,1011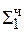

0, 0 101 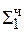1 ∙ 2^-1

⁺ 0,1011 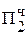= Мн b₃

1,0000 1 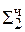(произошло переполнение)

0 ,1 000 01 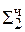∙ 2^-1 (коррекция)

0, 0 10 0001 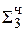∙ 2^-1 ( 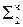∙ 2^-1) ∙ 2^-1

0, 0 010 0001 ∙ 2^-1 ((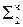 ∙ 2^-1)∙ 2^-1)∙ 2^-1

⁺ 1,0101 Δ = [- Мн]_доп (поправка)

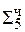1,0111 0001 =[Mн ∙ M_т]_доп

- 0,1000 1111 Mн ∙ Mт

В этом примере, а также в некоторых примерах, следующих ниже, происходит переполнение разрядной сетки, в результате которого искажаются и знаковая и значащая часть числа. Для коррекции (восстановления верного значения) производится немодифицированный сдвиг. В результате этого знаковый разряд сдвигается в значащую часть, а знаковый разряд меняет свое значение на противоположное.

3) Mн<0,

Mт>0.

Аналогично предыдущему случаю

[Мн∙Мт]_доп=2-Мн∙Мт,

Мн¢∙Мт= (1 - Мн)∙Мт= Мт - Мн∙Мт.

Таким образом, погрешность умножения равна разности [Мн Мт]_доп и Мт∙Мн¢.

Δ=2-Мн∙Мт- Мт + Мн∙Мт=2-Мт=[-Мт]_доп=[ [Мт]_доп]_доп.

Использовать этот вариант неудобно, так как нужно вводить поправку [-Mт]_доп в конце умножения, а в результате сдвигов Мт постепенно исчезает на регистре множителя и для поправки нужно либо вводить дополнительный регистр, либо вносить поправку в сумматор на первом такте умножения.

При этом знакосочетании возможно умножение без ввода поправки. Рассмотрим этот вариант на примере умножения по алгоритму Г (это справедливо и для других алгоритмов).

Мн∙Мт = А ∙ В = [ A ∙ b₁∙ 2^-1 ]_доп + [ A ∙ b₂∙ 2^-2 ]_доп+... + [A∙ b_n∙ 2^-n ]_доп.

На основании теоремы, доказывающей что сумма дополнительных кодов есть дополнительный код суммы, получаем

[ A ∙ b₁∙ 2^-1 + A ∙ b₂∙ 2^-2 +... + A∙ b_n∙ 2^-n ]_доп = [Мн ∙Мт]_доп.

В этом случае поправка вводится автоматически на каждом этапе умножения.

Пример: Mн = -0,1011

Mт = 0,1101

b₁…b_{4 4}

[Mн]_доп= 1,0101

0,00000000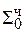

⁺ 1, 1 0101000 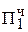= [Mн ∙ b₁ ∙ 2^-1]_доп

1,10101000

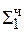
⁺ 1, 11 010100 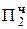= [Mн ∙ b₂ ∙ 2^-2]_доп

1,01111100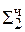

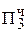⁺ 1, 1111 0101 = [Mн ∙ b₄ ∙ 2^-4]_доп

1,01110001 [Mн ∙ Mт]_доп

-0,10001111 Mн ∙ Mт

4) Mн<0,

Mт<0.

Mн ∙ Mт = 2 - [Mн ∙ Mт]_доп

[Mн]_доп ∙ (1 - Mт) = [Mн]_доп - [Mн]_доп ∙ Mт = [Mн]_доп - [Mн ∙ Mт]_доп

Δ=2 - [Mн ∙ Mт]_gдоп - [Mн]_доп + [Mн ∙ Mт]_доп = 2 - [Mн]_доп = [[Mн]_доп]_доп

Пример: Mн = - 0,1011 умножение будем выполнять

Mт = - 0,1101 по алгоритму умножения Г

[Mн]_доп = 1,0101

[Mт]_доп = 1,0011

Δ =[-Mн]_доп = 0,1011

0,00000000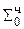

⁺ 1, 111 01010 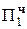= [Mн ∙ b₃ ∙ 2^-3]_доп

1,11101010

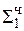
⁺ 1, 1111 0101 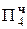= [Mн ∙ b₄ ∙ 2^-4]_доп

1,11011111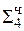

⁺ 0, 1011 0000 Δ (поправка)

0,10001111 [Mн∙ Mт]_доп

Дата добавления: 2014-12-26