Формы представления функций алгебры логики

Основными понятиями, лежащими в основе представления булевых функций в различных формах, являются понятия элементарной конъюнкции и элементарной дизъюнкции.

Элементарной конъюнкцией называется логическое произведение любого конечного числа различных между собой булевых переменных, взятых со знаком инверсии или без него.

Например, логические выражения вида x₁x₂x₃, x₁x₄, x₁x₂x₄ являются элементарными конъюнкциями, а выражения вида x₁x₂x₃, x₁x₄, x₁x₂x₄ не являются элементарными конъюнкциями.

Элементарной дизъюнкцией называется логическая сумма любого конечного числа различных между собой булевых переменных, взятых со знаком инверсии или без него

Примером логического выражения, являющегося элементарной дизъюнкцией, могут служить x₁+x₂+x₃, x₁+x₄, x₁+x₂+x₄, а выражения вида x₁+x₂+x₃, x₁+x₄, x₁+x₂+x₄ не являются элементарными дизъюнкциями.

Дизъюнктивной нормальной формой (ДНФ) булевой функции называется дизъюнкция конечного числа элементарных конъюнкций.

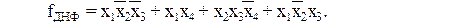
Число переменных, входящих в элементарную конъюнкцию, определяет ранг этой конъюнкции.

Совершенной ДНФ (СДНФ) логической функции от n аргументов называется такая ДНФ, в которой все конъюнкции имеют ранг n. СДНФ записывается по таблице истинности согласно правилу: для каждого набора переменных, на котором булева функция принимает единичное значение, записывается конъюнкция ранга n и все эти конъюнкции объединяются дизъюнктивно; переменная имеет знак инверсии, если на соответствующем наборе имеет нулевое значение.

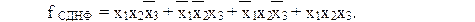
В общем виде это можно записать следующим образом:

,

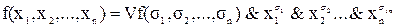где

Элементарные конъюнкции, образующие СДНФ, называют также конституентами (составляющими) единицы (минтерм), так как они соответствуют наборам, при которых функция принимает значение, равное единице. Построение СДНФ по таблице истинности называют составлением булевой функции по условиям истинности.

Конъюнктивной нормальной формой (КНФ) булевой функции называется конъюнкция конечного числа элементарных дизъюнкций.

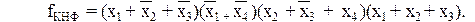
Совершенной КНФ (СКНФ) логической функции от n аргументов называется такая КНФ, в которой все дизъюнкции имеют ранг n. СКНФ записывается по таблице истинности согласно правилу: для каждого набора переменных, на котором булева функция принимает нулевое значение, записывается дизъюнкция ранга n и все эти дизъюнкции объединяются конъюнктивно; переменная имеет знак инверсии, если на соответствующем наборе имеет единичное значение.

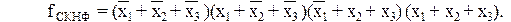
Элементарные дизъюнкции, образующие СКНФ, называют конституентами (составляющими) нуля (макстерм), так как они соответствуют наборам, при которых функция принимает нулевое значение. Построение СКНФ по таблице истинности называют составлением булевой функции по условиям ложности.

Теорема. Разложение в дизъюнкцию. Любую функцию f(x₁,...,x_m) для любого n (1 £ n £ m) можно представить в виде

f(x₁,...,x_m) = 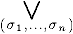x₁^s₁ &... & x_n^s_n & f(s₁,...,s_n,x_n+1,...,x_m).

Доказательство. Покажем, что для любого набора значений переменных (x₁,...,x_n,x_n+1,...,x_m) значения левой и правой частей совпадают. Возьмём фиксированный набор (x₁,...,x_n,x_n+1,...,x_m). Рассмотрим выражение x₁^s₁ &... & x_n^s_n. Если одно из значений x_i^s_i равно 0, то и всё выражение равно 0. Тогда и выражение x₁^s₁ &... & x_n^s_n & f(s₁,...,s_n,x_n+1,...,x_m) равно 0. Единице же выражение

x₁^s₁ &... & x_n^s_n равно только в том случае, если s₁ = x₁,..., s_n = x_n. При этом f(s₁,...,s_n,x_n+1,...,x_m) = f(x₁,...,x_n,x_n+1,...,x_m). Таким образом, значение правой части всегда равно f(x₁,...,x_m), то есть значению левой части.

Теорема. Разложение в конъюнкцию. Любую функцию f(x₁,...,x_m) для любого n (1 £ n £ m) можно представить в виде

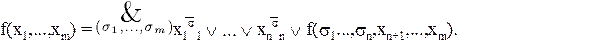Разложения по всем переменным дают суперпозицию конъюнкции, дизъюнкции и отрицания.

Дата добавления: 2014-12-26