Канонический метод структурного синтеза автоматов

Синтез цифровых устройств выполняется в два этапа:

§ этап абстрактного синтеза;

§ этап структурного синтеза.

Для перехода от абстрактного автомата к структурному требуется:

1) поставить в соответствие каждой букве входного алфавита Z=х{z₁,…,z_k} совокупность двоичных сигналов из множества X={x₁,x₂,…,x_L}, то есть закодировать входные символы абстрактного автомата. Значение L, определяющее количество двоичных переменных для кодирования абстрактных входных сигналов, вычисляется следующим образом: L=]log₂|Z|[, где |Z| - мощность множества Z (число различных элементов множества Z), ]n[ означает ближайшее целое число, большее либо равное n;

2) поставить в соответствие каждому символу выходного алфавита W={w₁,…,w_l} совокупность двоичных выходных сигналов из множества Y={y₁,y₂,…,y_N}, то есть закодировать выходные символы абстрактного автомата. Значение N вычисляется следующим образом: N=]log₂|W|[;

3) поставить в соответствие каждому состоянию абстрактного автомата А={a_a,…,a_m} совокупность состояний элементов памяти T={t₁,t₂,…,t_r}, то есть закодировать состояния абстрактного автомата. Количество элементов памяти определяется условием r=]log₂|А|[;

4) составить систему уравнений для функций y₁,y₂,…,y_N,d₁,d₂,…,d_r, в соответствии с которой будет построена комбинационная часть структурной схемы автомата.

Полученная таким образом система логических функций называется канонической.

Рассмотрим пример структурного синтеза автомата Мили, блок памяти которого будет построен на Т-триггерах. Исходные данные для выполнения синтеза структурной схемы заданы таблично. Это таблица переходов (табл.32)и таблица выходов (табл.33). Описание работы Т-триггера приведено в табл. 29.

Определяем вначале общее количество входов, выходов и элементов памяти автомата:

L=]log₂|Z|[ = ]log₂4[=2;

N=]log₂|W|[= ]log₂6]=3;

r=]log₂|А|[ = ]log₂4[=2.

Структурная схема автомата изображена на рис. 43.

На основании полученных значений построим таблицы и выполним кодирование входных, выходных символов и состояний исходного автомата (табл. 34-36).

По результатам кодирования строим таблицы переходов и выходов структурного автомата (табл. 37 и 38 соответственно). Они получаются путем занесения соответствующих значений из табл. 34-36 в исходные таблицы (см. табл. 32, 33).

На основании табл. 37, используя таблицу переходов Т-триггера (см. табл. 29) построим табл. 39 − таблицу функций возбуждения элементов памяти.

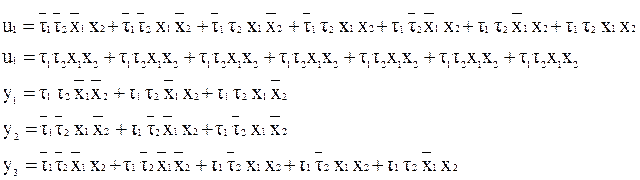Если i-й триггер на некотором переходе переключается из состояния 0 в состояние 1 или наоборот, то u_i=1, в противном случае (то есть если i-й триггер не переключается) u_i=0. Например, рассмотрим переход из состояния 10 в состояние 11 (см. табл. 37, 4-й столбец, 3-я строка). Первый триггер (установленный в 1) не меняет своего значения, поэтому функция возбуждения элемента памяти для него u₁=0. Второй триггер изменяет свое значение с 0 на 1, следовательно, u₂=1. Остальные клетки табл. 39 заполняются аналогично. На основании табл. 38 и 39 запишем систему логических функций для построения комбинационной схемы автомата:

Для упрощения комбинационной схемы выполним минимизацию каждой из логических функций. Для этого используем метод минимизирующих карт Карно. На рис. 44 изображены пять карт Карно для минимизации каждой из пяти логических функций.

По результатам минимизации запишем систему минимальных функций:

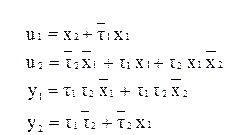
На рис. 45 изображена логическая схема, построенная на основании полученной системы булевых функций. При построении схемы использованы элементы ”И” и ”ИЛИ”.

Дата добавления: 2014-12-26