Определение приведенных масс и сил графоаналитическими методами

Приведенные массы могут быть определены по формулам (16), (17), а силы как по формулам (23), (24), так и на основании теоремы Жуковского.

Методику расчета приведенных масс и сил по указанным формулам рассмотрим на примере кривошипно-ползунного механизма (рис. 4, а). Для заданного положения этого механизма необходимо определить либо приведенные к оси А вращения кривошипа момент инерции J_П и момент сил М_П, либо приведенные к точке В кривошипа массу m_П и силу . В качестве исходных данных заданы: массы m₁, m₂, m₃ звеньев 1, 2, 3 и положения их центров масс S₁, S₂, S₃; моменты инерции 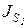, 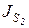кривошипа 1 и шатуна 2 относительно осей, проходящих через их центры масс перпендикулярно плоскости движения; векторы линейных скоростей центров масс , , (); угловые скорости , кривошипа и шатуна. На механизм действуют внешние силы и моменты сил: сила 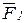, приложенная к кривошипу в точке К₁; сила , приложенная к шатуну в точке К₂; сила 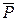, приложенная к ползуну 3; момент М₂, приложенный к шатуну 2, и силы веса звеньев , , .

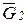Рисунок 4 – К определению приведенных сил кривошипно-ползунного механизма: а – план механизма; б – план скоростей; в – рычаг Жуковского

Углы между векторами сил и скоростей точек их приложения обозначены буквой a, у которой нижний индекс является номером звена, а верхний - обозначением силы.

Задача определения приведенного момента инерции J_П и приведенного момента сил М_П кривошипно-ползунных механизмов возникает при их динамическом синтезе как при использовании механизмов для преобразования вращательного движения кривошипа 1 в возвратно-поступательное движение ползуна 3, например, в воздушных компрессорах, кривошипных прессах или ковочных машинах, так и при использовании для преобразования возвратно-поступательного движения ползуна во вращательное движение кривошипа, например, в паровых машинах или двигателях внутреннего сгорания. При этом в обоих случаях за звено приведения и начальное звено принимают кривошип.

Для определения приведенного момента инерции J_П механизма вначале по формуле Гюйгенса-Штейнера вычисляют момент инерции J₀₁ кривошипа относительно оси вращения А:

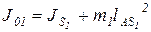, (38)

где – расстояние между центрами масс S₁ кривошипа и осью его вращения.

Если центр масс S₁ совпадает с осью вращения А, то J₀₁ = . Подставляя выражение (38) в формулу (16), для каждого положения механизма получаем

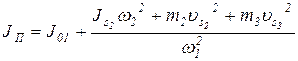. (39)

Для определения приведенного момента сил М_П на плане механизма показывают приложенные к нему приводимые силы и моменты сил (рис. 4, а). Строят план скоростей (рис. 4, б) и в точках К₁ и К₂ приложения сил 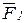, и в центрах масс S₁, S₂, S₃ приложения сил веса , , 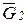на плане механизма прикладывают полученные на плане скоростей векторы скоростей 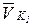, , 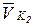, , 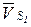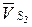этих точек. Приведенные сила и момент 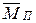для каждого положения механизма определяются по формулам (23) и (24).

При определении и 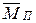знаки членов, входящих в правую часть этих формул и определяющих знаки мощностей приводимых сил 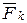, зависят от знаков косинусов углов между направлениями векторов сил и скоростей точек их приложения. Для правильного учета знаков начала этих векторов следует перенести по линиям их действия в точку пересечения этих линий и по углу между векторами определить знак мощности силы. Если угол между векторами силы и скорости будет острым, косинус этого угла и знак мощности приводимой силы будут положительными, если тупым - отрицательными. Из схемы механизма (рис. 4, а) следует, что угол между вектором силы 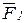и скорости 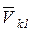точки ее приложения является острым, а углы , , между векторами сил , , 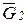и скоростей , , являются тупыми. 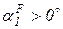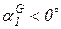Соответственно подставляемые в уравнения (23) и (24) значения косинусов будут cos ; cos ; cos ; cos .

При направлении векторов силы и скорости точки ее приложения по одной линии угол между векторами может быть равен 0° или 180°, соответственно косинусы этих углов равны 1 или -1. В первом случае направления векторов силы и скорости совпадают, как например векторов силы и скорости 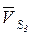ползуна 3 (см. рис. 4, а), во втором – направления векторов противоположны.

Знаки косинусов углов между векторами сил и скоростей точек их приложения, т.е. знаки мощностей сил, можно определить следующим образом.

Проецируют заданные силы и силы веса звеньев на линии действия векторов скоростей точек их приложения. Проекция силы 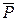не обозначена, так как она совпадает с направлением скорости точки приложения этой силы. Проекция силы 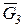равна нулю. Знаки мощности сил в выражениях (23), (24) определяют по направлению проекций векторов сил и векторов скоростей точек их приложения. Мощность считается положительной, если направления проекций векторов сил и скоростей точек их приложения совпадают. В этом случае приведенные моменты от этих сил на звене приведения совпадают с направлением угловой скорости звена. В рассматриваемом примере положительные мощности создают силы 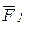и 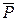. Если проекции векторов сил на линию действия векторов скоростей точек их приложения и векторы скоростей направлены в противоположные стороны, мощности этих сил считаются отрицательными, и приведенные моменты от этих сил направлены противоположно угловой скорости звена приведения. К таким силам относятся сила и силы веса , 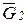. Мощность силы 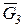равна нулю.

Мощность момента М_2, действующего на звено 2

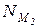= М₂ω_{2 .} (40)

Знак мощности момента М₂ определяется следующим образом. На схеме механизма показывают направление угловой скорости звена 2 (шатуна) при его относительном движении (повороте) вокруг точки В. Это направление определяют, мысленно перенося к точке С на плане соответствующего положения механизма вектор 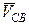скорости точки С относительно точки В, изображенный на плане скоростей (рис. 4, б) отрезком (вс). В данном примере угловая скорость направлена по часовой стрелке. По направлению определяется знак мощности момента М₂. Если направление момента М₂ совпадает с направлением , мощность момента в выражениях (23), (24) принимается положительной. В этом случае момент М₂ по направлению совпадает также с угловой скоростью звена приведения. Если момент М₂ направлен противоположно угловой скорости , как в рассматриваемом примере, значение мощности 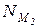принимается отрицательным и момент М₂ направлен противоположно угловой скорости ω₁ звена приведения.

Подставляя значения мощностей сил и момента М_{2 ,} приложенных к механизму, в выражение (24) с учетом их знаков, находим значение приведенного к кривошипу момента сил

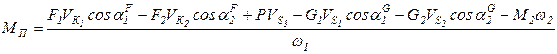. (41)

Если полученное значение М_П окажется отрицательным, его направление будет противоположным угловой скорости начального звена (кривошипа 1).

Направление приведенной силы выбирается по направлению приведенного момента М_П.

Приведенная сила и приведенный момент сил могут быть определены также по методу Жуковского с построением повернутого на 90˚ плана скоростей. При этом выбор направления поворота не влияет на результат решения. Метод Жуковского основан на теореме Жуковского, которая гласит: если силу, приложенную в какой либо точке звена механизма, перенести параллельно самой себе в одноименную (сходственную) точку повернутого плана скоростей, то момент этой силы относительно полюса повернутого плана скоростей будет пропорционален ее мощности. Повернутый план скоростей с приложенными к нему силами рассматривается как некоторый рычаг с опорой в полюсе плана скоростей, который получил название рычага Жуковского.

Определим приведенный момент М_П с помощью рычага Жуковского для рассматриваемого кривошипно-ползунного механизма. Для этого построим повернутый по часовой стрелке план скоростей с приложенными в сходственных точках силами (см. рис. 4, в). Следует подчеркнуть, что при определении приведенного момента сил М_П с помощью рычага Жуковского внешние моменты сил, действующие на звенья механизма, нельзя переносить непосредственно на соответствующие отрезки повернутого плана скоростей. Знаки перенесенного и заданного моментов совпадают при одинаковом расположении соответствующих точек плана положения и повернутого плана скоростей при обходе в одном направлении. Иначе момент учитывается с противоположным знаком. Поэтому план скоростей удобно поворачивать на 90˚ в направлении, обеспечивающем сохранение расположения характерных точек при обходе в одном направлении. При использовании рычага Жуковского моменты, приложенные к звеньям, заменяют парами сил и силы этих пар переносят в сходственные точки повернутого плана скоростей. Обычно пары сил прикладывают в кинематических парах, соединяющих звено, на которое действует момент, с другими звеньями механизма. 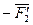В нашем случае момент заменяем парой сил , , действующих в направлении создания момента , приложенных в кинематических парах В и С перпендикулярно звену ВС. Модули сил определяются из условия:

, (42)

где 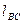– длина шатуна ВС.

В случае, если внешний момент прикладывается к звену, совершающему только вращательное движение, например к кривошипу или коромыслу, соединенным со стойкой, одна из сил пары, заменяющей момент, прикладывается к неподвижной кинематической паре, соединяющей звено со стойкой.

В рассматриваемом примере (см. рис.4, в) поворот плана скоростей выполнен на 90˚ по часовой стрелке. При таком повороте направление момента пары сил на плане скоростей не совпадает с направлением момента на плане механизма: момент на плане механизма (см. рис. 4, а) действует против часовой стрелки, а на повернутом плане скоростей (см. рис. 4, в) момент от заменяющей его пары сил и - - по часовой стрелке.

С помощью повернутого плана скоростей просто доказывается теорема Жуковского. Например, момент силы , приложенной в точке 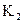повернутого плана скоростей, относительно полюса «р»

,

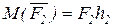где – плечо силы 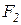относительно полюса.

В этой формуле ; отрезок ,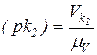

где – масштабный коэффициент скорости.

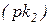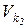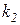Угол между отрезком , изображающим скорость точки приложения силы , и плечом равен углу на плане механизма (рис. 4, а) по взаимной перпендикулярности сторон. Тогда выражение для принимает вид

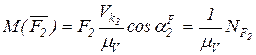, (43)

где – мощность силы F₂.

Полученное соотношение определяет доказательство теоремы Жуковского: момент силы относительно полюса повернутого плана скоростей пропорционален ее мощности. Коэффициентом пропорциональности является постоянная величина 1/ m_V.

Исходя из условия равенства мощности приведенной силы F_П сумме мощностей приводимых сил, т.е. равенства момента приведенной силы сумме моментов приводимых сил относительно полюса повернутого плана скоростей, выражение для определения приведенной силы будет иметь вид

. (44)

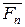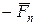Приведенный момент сил М_П на схеме механизма и повернутом плане скоростей представлен в виде пары приведенных сил и , приложенных соответственно в точках А, В и «р», «в» перпендикулярно отрезкам АВ и (рв). Величина приведенного момента определяется по соотношению

, (45)

где l_АВ – длина кривошипа.

Направление приведенного момента М_П на схеме механизма (см. рис.4, а) определяется по направлению момента приведенной силы 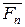относительно точки А, то есть против часовой стрелки.

Результаты определения приведенных моментов по формулам (41) и (45) должны совпадать. Эти формулы могут служить для взаимопроверки правильности определения приведенного момента сил, действующих на звенья механизма.

Дата добавления: 2014-12-26