Волновой характер электромагнитного поля

Электромагнитное поле, возникающее в некоторой области пространства, не заполняет его мгновенно, а распространяется с конечной скоростью, зависящей от свойств среды. При распространении периодического процесса с конечной скоростью происходит запаздывание его по фазе, следствием этого является волновой характер распространения.

Докажем волновой характер электромагнитного поля математически, сводя уравнение Максвелла к уравнениям известного вида, которые заведомо описывают волновой процесс.

Первые два уравнения Максвелла в комплексном виде: 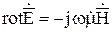и 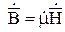могут быть приведены к одному. Для этого применим операцию rot к правой и левой частям первого уравнения:

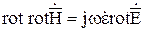. (10.69)

Отсюда с помощью второго уравнения можно исключить :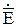

. (10.70)

Пусть среда изотропна и однородна и плотность зарядов r отсутствует (r=0). Используем известное соотношение

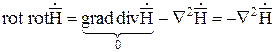; (10.71)

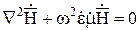, (10.72)

где 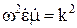, k – постоянная распространения электромагнитной волны (иногда используются термины «фазовая постоянная», «волновое число»).

Аналогично можно получить уравнение относительно :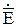

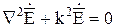. (10.73)

Уравнения (10.72) и (10.73) в математической физике называются уравнениями Гельмгольца (волновыми уравнениями). Эти уравнения описывают стационарные волновые процессы, то есть распространение в пространстве волн с некоторой постоянной частотой. Таким образом, переменность во времени электрических или магнитных полей неизбежно приводит к распространению в пространстве электромагнитных волн.

Получим простейшее решение волнового уравнения и выясним его физический смысл.

В системе координат, изображенной на рис. 10.13, исследуемая область V лежит далеко от источника O, так что любые две ее точки, расположенные на перпендикулярной к оси OZ площадке, можно считать находящимися на одинаковых расстояниях от O. Тогда можно считать отрезки OM₁ и OM₂ равными и параллельными, т.е. точки M₁ и M₂ по отношению к источнику совершенно равноправны. Тогда изменениями электромагнитного поля от OM₁ к OM₂ можно пренебречь и считать, что во всей области V процесс не зависит от координат х и у:

.

Отсюда вытекает упрощение оператора Лапласа

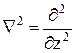(10.74)

и волнового уравнения

. (10.75)

Решение такого уравнения известно:

. (10.76)

Здесь и 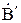– произвольные коэффициенты, включающие множитель e^jwt; – единичный вектор, указывающий направление .

Выделим временной множитель:

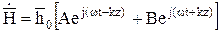(10.77)

и, выделив вещественную часть, получим выражение вектора :

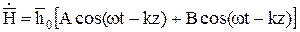(10.78)

(коэффициенты А и В считаем вещественными).

В момент времени t₁ магнитное поле, выражаемое первым членом (10.78), распределяется вдоль оси z по закону: Acos(wt₁-kz), а по прошествии времени Dt в момент t₂= t₁+Dt это распределение примет вид: Acos(wt₁+wDt-kz), т.е. окажется смещенным в положительном направлении на расстояние Dz, которое легко определить из условия wDt-kz=0. Отсюда с учетом k²=w²em найдем скорость перемещения Dz/Dt, которая равна фазовой скорости волны

. (10.79)

То есть гармоническое распределение поля непрерывно перемещается в направлении положительной оси z с постоянной скоростью u. Это – бегущая волна, а u – ее фазовая скорость. В вакууме u=c=1/e₀m₀=2,998·10⁸ м/с.

В среде с проницаемостями e и m фазовая скорость волны меньше в раз. Длина волны

. (10.80)

Второй член уравнения (10.78) отличается только знаком при k, следовательно, соответствует волне, распространяющейся со скоростью (-u), т.е. в противоположном направлении. В рассмотренном примере обратная волна должна отсутствовать (В=0). Найденная волна является плоской и однородной. «Плоская» волна означает, что в любой плоскости z=const в заданный момент времени фаза процесса постоянна. С течением времени плоскость постоянной фазы перемещается в направлении распространения волны со скоростью u и называется фронтом волны. «Однородная» волна означает, что амплитуда волны постоянна (не зависит от координат).

Сферические волны возбуждаются точечным источником. Они имеют волновые фронты в виде концентрических сфер.

Цилиндрические волны возбуждаются бесконечной нитью. Они имеют волновые фронты в виде цилиндров.

Дата добавления: 2014-12-26