Отражение и преломление электромагнитных волн

Вакуум

Плоские волны в однородных неограниченных средах

Фазовая скорость в вакууме определяется по общей формуле u_ф=w/k. Поскольку волновое число в вакууме 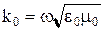, то

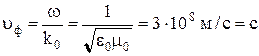, (10.107)

то есть скорость произвольной электромагнитной волны в вакууме равна скорости света независимо от частоты волны. Среды, в которых фазовая скорость не зависит от частоты, называют средами без дисперсии.

Волновое сопротивление в вакууме

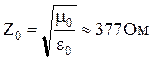. (10.108)

2. Диэлектрик без потерь

Рассмотрим случай немагнитного диэлектрика с m=1:

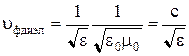, (10.109)

то есть фазовая скорость, а следовательно и длина волны в диэлектрике, уменьшается в 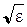раз по сравнению с вакуумом.

3. Диэлектрик с потерями

Для такой среды необходимо воспользоваться комплексной диэлектрической проницаемостью

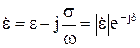, (10.110)

где ; .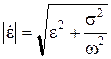

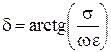Комплексная постоянная распространения:

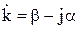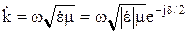; . (10.111)

Преобразуя по формуле Эйлера, получаем фазовую постоянную и постоянную затухания:

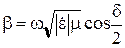; (10.112)

. (10.113)

Реальные диэлектрики характеризуются очень малыми углами потерь, поэтому можно считать, что ; ; .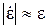

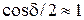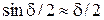Тогда

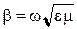; (10.114)

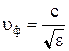; (10.115)

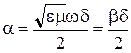. (10.116)

Таким образом, при расчетах фазовых соотношений в первом приближении можно не учитывать потери в материале. С другой стороны, коэффициент затухания амплитуды плоских волн в неидеальном диэлектрике прямо пропорционален углу диэлектрических потерь.

4. Волны в хорошо проводящих средах

Среда считается хорошо проводящей, если в такой среде плотность токов проводимости намного больше плотности токов смещения:

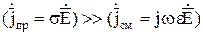или s/w>>e,

то есть мнимая часть комплексной диэлектрической проницаемости должна быть значительно больше вещественной. Причем чем ниже частота, тем ближе среда к идеальному проводнику.

В этом случае вещественной частью комплексного параметра можно пренебречь и считать этот параметр чисто мнимым:

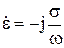. (10.117)

Постоянная распространения 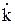тогда запишется как

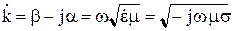. (10.118)

Так как 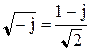, то можно переписать:

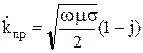, (10.119)

откуда

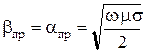, (10.120)

следовательно, длина волны в проводнике

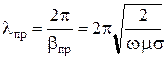. (10.121)

Длина волны в проводнике сильно уменьшается по сравнению с длиной волны в свободном пространстве:

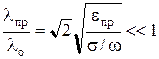. (10.122)

Следовательно, в металле снижается и фазовая скорость волн.

Амплитуда электромагнитной волны в среде с потерями уменьшается по закону 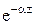. Расстояние d, на котором амплитуда волны падает в 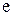раз по сравнению с её начальным уровнем, называется глубиной проникновения или глубиной поверхностного слоя. Это расстояние, очевидно, удовлетворяет соотношению ad=1, откуда

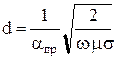. (10.123)

На таком расстоянии от поверхности волна затухает в 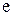раз, то есть поле существует только в приповерхностном слое. Это явление называется скин-эффектом.

Пусть плоская электромагнитная волна падает на плоскую границу раздела двух сред под произвольным углом j (0°£j£90°). При анализе введем три волны: падающую, отраженную и преломленную (см. рис. 10.18).

Векторы Пойнтинга 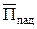, 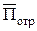и 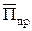всех трёх волн лежат в одной плоскости YOZ, называемой плоскостью падения; 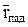, 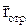и 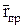– текущие координаты фронтов соответствующих волн; e₁, m₁, k₁ – параметры первой среды; e₂, m₂, k₂ – параметры второй среды.

Модули r_пад, r_отр и r_пр можно выразить через соответствующие углы j_пад, j_отр, j_пр и координаты y и z:

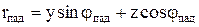; (10.124)

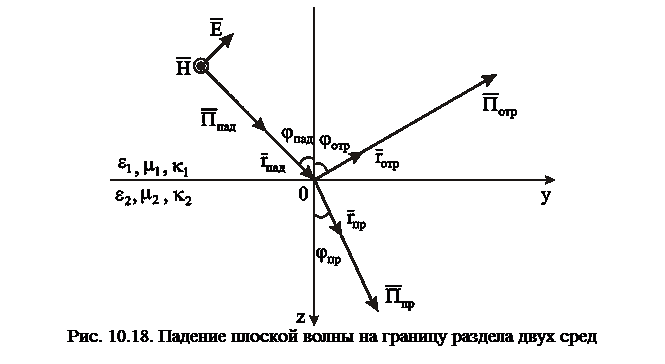
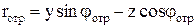; (10.125)

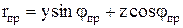. (10.126)

Тогда комплексные амплитуды падающей, отраженной и преломленной волн запишутся соответственно:

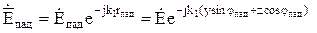; (10.127)

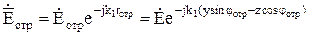; (10.128)

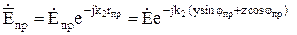. (10.129)

На границе раздела, то есть в плоскости z=0, должны выполняться граничные условия 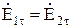и .

Тогда

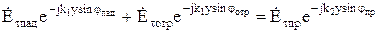.(10.130)

Чтобы условие на границе для 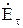соблюдалось для всех y, нужно, чтобы показатели экспонент были одинаковы:

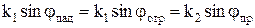. (10.131)

Отсюда два условия:

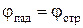(10.132)

и

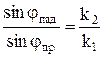. (10.133)

Введем показатель 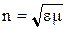– показатель преломления данной среды, характеризующий её оптическую плотность.

Тогда справедливо равенство:

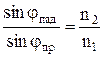. (10.134)

Рассмотренные закономерности справедливы для любой ориентации векторов поля к плоскости падения.

Рассмотрим случай падения волны на границу раздела двух сред, когда одна из сред представляет собой проводник. В случае идеального проводника s=¥, поле E=0. Комплексный параметр 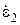во второй среде стремится к бесконечности:

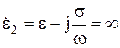. (10.135)

При этом

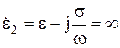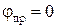; , (10.136)

то есть преломленная волна стремится вглубь проводника по нормали к его поверхности. Но, с другой стороны, поле в идеальном проводнике равно нулю, то есть волна полностью отражается:

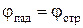. (10.137)

Так как граничные условия для 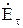на поверхности идеального проводника 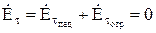, то .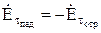

Граничные условия для нормальных составляющих поля:

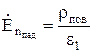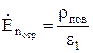; , то есть .

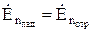Следовательно, при падении на границу раздела с идеальным проводником волна затухает в бесконечно тонком приповерхностном слое.

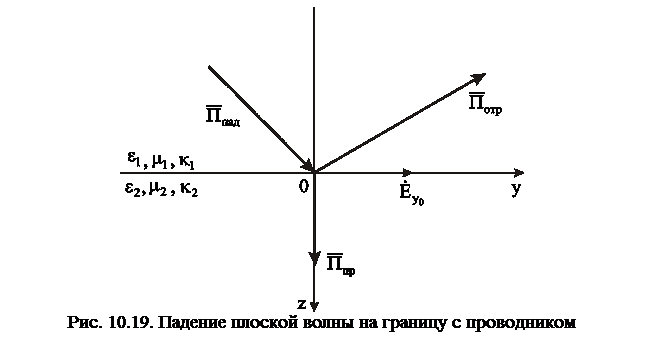Теперь рассмотрим падение электромагнитной волны на реальный проводник. Как уже было показано, в проводнике будут возникать плоские волны, уходящие вглубь проводника по нормали к поверхности раздела (в направлении оси z). В случае конечной проводимости на границе раздела появляется не равная нулю составляющая E_t. Она направлена вдоль оси y, назовем её 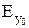(рис. 10.19). Тогда выражения для комплексных амплитуд векторов поля в проводнике запишутся следующим образом:

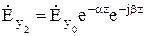; (10.138)

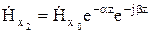. (10.139)

По мере проникновения волны вглубь проводника её амплитуда убывает по экспоненциальному закону. Скорость уменьшения амплитуды определяется величиной коэффициента затухания a. Чем лучше проводник, тем больше a, таким образом, в хорошо проводящих средах поле оказывается сосредоточенным лишь в очень тонком приповерхностном слое («скин-эффект»).

Определим плотность тока в проводнике:

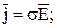
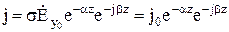, (10.140)

где 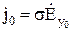– плотность тока на поверхности проводника. По мере удаления от поверхности проводника плотность тока убывает по тому же закону, что и амплитуда напряженности поля:

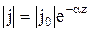. (10.141)

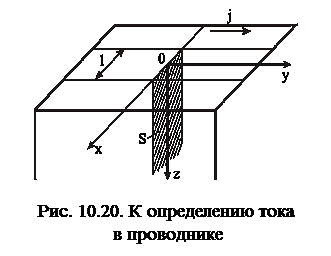
Определим величину тока, текущего через поперечное сечение проводника на единицу ширины проводника l=1 м (рис. 10.20):

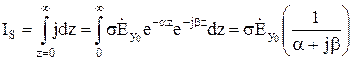. (10.142)

Учитывая, что для проводников a=b

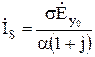. (10.143)

Величина 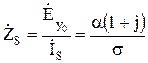называется удельным поверхностным сопротивлением проводника.

С учетом (10.143) запишем:

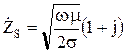. (10.144)

Это сопротивление имеет комплексный активно-индуктивный характер и определяет потери мощности на единицу площади проводника.

Дата добавления: 2014-12-26