
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгебра и геометрия 8 страница
|
|
|
|
18 вариант. 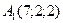 ,
, 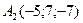 ,
, 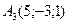 ,
, 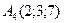 .
.
19 вариант. 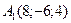 ,
,  ,
, 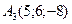 ,
, 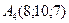 .
.
20 вариант.  ,
, 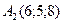 ,
, 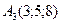 ,
,  .
.
21 вариант. 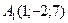 ,
, 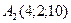 ,
, 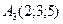 ,
, 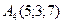 .
.
22 вариант. 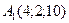 ,
, 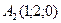 ,
, 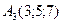 ,
, 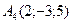 .
.
23 вариант. 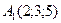 ,
,  ,
,  ,
, 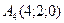 .
.
24 вариант. 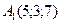 ,
,  ,
, 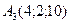 ,
, 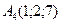 .
.
25 вариант. 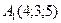 ,
,  ,
, 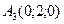 ,
, 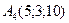 .
.
26 вариант. 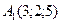 ,
, 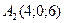 ,
, 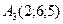 ,
,  .
.
27 вариант. 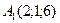 ,
,  ,
, 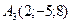 ,
, 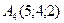 .
.
28 вариант.  ,
, 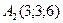 ,
,  ,
,  .
.
29 вариант.  ,
, 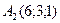 ,
,  ,
, 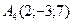 .
.
30 вариант. 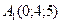 ,
,  ,
, 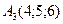 ,
, 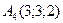 .
.
Задание 21. Построить кривые и записать их уравнения.
1. Окружность а) с центром в т. 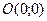 и радиусом
и радиусом 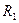 ;
;
б) с центром в т. 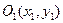 и радиусом
и радиусом 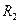 .
.
2. Эллипс а) с центром в т. 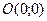 и полуосями
и полуосями 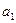 и
и 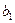 ;
;
б) с центром в т. 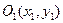 и полуосями
и полуосями 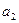 и
и 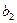 .
.
3. Гипербола а) с центром в т. 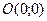 и полуосями
и полуосями 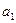 - действительной,
- действительной, 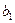 - мнимой и
- мнимой и
сопряженную с ней гиперболу;
б) с центром в т. 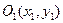 и полуосями
и полуосями 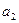 - действительной,
- действительной, 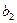 - мнимой
- мнимой
4. Парабола а) с вершиной в т. 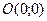 , параметром
, параметром 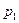 , ветви которой направлены
, ветви которой направлены
- вправо,
- влево,
- вверх,
- вниз;
б) с вершиной в т. 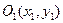 и параметром
и параметром 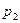 , ветви направлены вниз.
, ветви направлены вниз.
| № вар. | 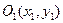
| 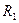
| 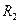
| 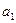
| 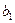
| 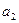
| 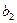
| 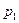
| 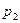
|
| (1;–2) | |||||||||
| (3;0) | |||||||||
| (–2;3) | |||||||||
| (–1; 2) | |||||||||
| (4, 5) | |||||||||
| (5, 3) | |||||||||
| (5, 3) | |||||||||
| (3, 5) | |||||||||
| (3, 2) | |||||||||
| (–2, 1) | |||||||||
| (4, 0) | |||||||||
| (4, 5) | |||||||||
| (6, 1) | |||||||||
| (1, 2) | |||||||||
| (1, –1) | |||||||||
| (4, 5) | |||||||||
| (3, 4) | |||||||||
| (4, –2) | |||||||||
| (0, –3) | |||||||||
| (–2, 5) | |||||||||
| (–3, 1) | |||||||||
| (4, –1) | |||||||||
| (3, 2) | |||||||||
| (0, 4) | |||||||||
| (–2, –3) | |||||||||
| (–1, 2) | |||||||||
| (1, –2,) | |||||||||
| (–2, –4) | |||||||||
| (4, 6) | |||||||||
| (3, 5) |
Задание 22. Решить задачи и построить фигуры.
1 вариант. Составить канонические уравнения: а) параболы, если ее фокус имеет координаты (0; –3); б) эллипса, если его эксцентриситет 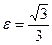 , большая полуось а = 3; в) гиперболы, если расстояние между фокусами равно 10, а расстояние между вершинами равно 8.
, большая полуось а = 3; в) гиперболы, если расстояние между фокусами равно 10, а расстояние между вершинами равно 8.
2 вариант. Составить канонические уравнения: а) эллипса, зная, что расстояние между фокусами равно 24 и большая полуось равна 26; б) гиперболы, если действительная полуось равна 5 и эксцентриситет 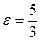 3; в) параболы, директриса которой имеет уравнение x + 2 = 0.
3; в) параболы, директриса которой имеет уравнение x + 2 = 0.
3 вариант. Составить канонические уравнения: а) эллипса, если большая полуось равна 5, а расстояние между фокусами – 8; б) гиперболы, если она равносторонняя и проходит через точку M (2, 1); в) параболы, фокус которой имеет координаты (–5, 0).
4 вариант. Составить канонические уравнения: а) эллипса, если большая полуось равна 10 и эксцентриситет равен 0,8; б) гиперболы, асимптоты которой заданы уравнениями y=± 2 x и фокусы находятся на расстоянии равном 5 от центра; в) параболы, симметричной относительно оси ординат и проходящей через точку М (5, 1).
5 вариант. Составить канонические уравнения: а) эллипса, если эксцентриситет 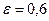 , а расстояние между фокусами равно 6; б) гиперболы, если расстояние между фокусами равно 10, а расстояние между вершинами – 8; в) параболы, директриса которой имеет уравнение у + 6 = 0.
, а расстояние между фокусами равно 6; б) гиперболы, если расстояние между фокусами равно 10, а расстояние между вершинами – 8; в) параболы, директриса которой имеет уравнение у + 6 = 0.
6 вариант. Составить канонические уравнения: а) эллипса, расстояние, между директрисами которого равно 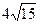 , а
, а 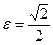 ; б) гиперболы, если расстояние между директрисами равно 8/5 и эксцентриситет
; б) гиперболы, если расстояние между директрисами равно 8/5 и эксцентриситет  ; в) параболы, если она проходит через точку (–4, 4) и симметрична относительно оси Ох.
; в) параболы, если она проходит через точку (–4, 4) и симметрична относительно оси Ох.
7 вариант. Составить канонические уравнения: а) эллипса, расстояние, между директрисами которого равно 12, а большая ось равна 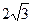 ; б) параболы, симметричной относительно оси абсцисс и проходящей через точку М (–1, 2); в) Найти длины осей, координаты фокусов и эксцентриситет гиперболы, заданной каноническим уравнением
; б) параболы, симметричной относительно оси абсцисс и проходящей через точку М (–1, 2); в) Найти длины осей, координаты фокусов и эксцентриситет гиперболы, заданной каноническим уравнением 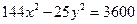 .
.
8 вариант. а) Составить канонические уравнения: а) эллипса, если его эксцентриситет 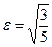 , а малая полуось b = 2; б) параболы, симметричной относительно оси ординат и проходящей через точку
, а малая полуось b = 2; б) параболы, симметричной относительно оси ординат и проходящей через точку  ; в) Найти длины осей, координаты фокусов и эксцентриситет гиперболы, заданной каноническим уравнением
; в) Найти длины осей, координаты фокусов и эксцентриситет гиперболы, заданной каноническим уравнением  .
.
9 вариант. Составить канонические уравнения: а) эллипса, расстояние, между фокусами которого равно 8, а эксцентриситет 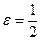 ; б) гиперболы, действительная полуось которого равна 20, и гипербола проходит через точку N (–10, 4); в) параболы, фокус которой имеет координаты (0, –3).
; б) гиперболы, действительная полуось которого равна 20, и гипербола проходит через точку N (–10, 4); в) параболы, фокус которой имеет координаты (0, –3).
10 вариант. Составить канонические уравнения: а) эллипса, сумма полуосей которого равна 18 и расстояние между фокусами – 12; б) гиперболы, если даны уравнения ее асимптот y=± 5 x /12 и координаты точки М (24, 5), лежащей на гиперболе; в) параболы, директриса которой имеет уравнение х – 15 = 0.
11 вариант. Составить канонические уравнения: а) параболы, симметричной относительно оси Оx, с вершиной в начале координат и проходящей через точку А (–2, –3); б) эллипса, если его большая полуось равна 12, а эксцентриситет равен 0,8; в) гиперболы проходящей через точку ( ) и имеющей мнимую полуось равную 2.
) и имеющей мнимую полуось равную 2.
12 вариант. Составить канонические уравнения: а) эллипса, если малая полуось равна 24, а расстояние между фокусами 2 с = 10; б) гиперболы, если расстояние между фокусами равно 6 и эксцентриситет  ; в) параболы, расположенной в правой полуплоскости симметрично относительно оси Оx, если ее параметр р = 3.
; в) параболы, расположенной в правой полуплоскости симметрично относительно оси Оx, если ее параметр р = 3.
13 вариант. Составить канонические уравнения: а) гиперболы, если уравнения асимптот y=± 4 x / 3 и расстояние между фокусами 2 с = 20; б) эллипса, если расстояние между фокусами 2 с = 6 и эксцентриситет 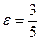 ; в) параболы, симметричной относительно оси Оx и проходящей через точку
; в) параболы, симметричной относительно оси Оx и проходящей через точку
А (9; 6).
14 вариант. Составить канонические уравнения: а) гиперболы, если ее расстояние между фокусами 2 с = 10 и мнимая ось равна 8; б) параболы, которая имеет фокус F (0; –3), проходит через начало координат и симметрична относительно оси ординат; в) эллипса, если большая ось равна 10, а расстояние между фокусами – 8.
15 вариант. Составить канонические уравнения: а) эллипса, если его полуоси равны соответственно 7 и 2; б) гиперболы, фокусы которой лежат на оси абсцисс, симметрично относительно начала координат и даны точки 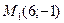 и
и 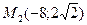 , принадлежащие гиперболе; в) параболы, расположенной в нижней плоскости симметрично относительно оси Оу и ее параметр равен 3.
, принадлежащие гиперболе; в) параболы, расположенной в нижней плоскости симметрично относительно оси Оу и ее параметр равен 3.
16 вариант. Составить канонические уравнения: а) гиперболы, имеющей вершины в фокусах, а фокусы в вершинах эллипса 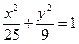 ; б) эллипса, если расстояние между фокусами равно 24, и эксцентриситет равен
; б) эллипса, если расстояние между фокусами равно 24, и эксцентриситет равен 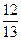 ; в) параболы, симметричной относительно оси абсцисс и проходящей через точки (0, 0) и (1, –3).
; в) параболы, симметричной относительно оси абсцисс и проходящей через точки (0, 0) и (1, –3).
17 вариант. Составить канонические уравнения: а) параболы, расположенной симметрично относительно оси абсцисс и проходящей через точку В (–1; 3); б) гиперболы, фокусы которой лежат на оси абсцисс, симметрично относительно начала координат и даны координаты точки 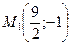 , принадлежащей гиперболе, и уравнения асимптот
, принадлежащей гиперболе, и уравнения асимптот 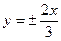 ; в) эллипса, фокусы которого расположены на оси абсцисс, симметрично относительно начала координат, если даны точка
; в) эллипса, фокусы которого расположены на оси абсцисс, симметрично относительно начала координат, если даны точка 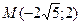 , принадлежащая эллипсу, и его малая ось равная 3.
, принадлежащая эллипсу, и его малая ось равная 3.
18 вариант. Составить канонические уравнения: а) эллипса, фокусы которого расположены на оси абсцисс, симметрично относительно начала координат, если даны точки  и
и 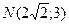 принадлежащие эллипсу; б) гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, кроме того, расстояние между ними 20, а эксцентриситет
принадлежащие эллипсу; б) гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, кроме того, расстояние между ними 20, а эксцентриситет 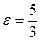 ; в) параболы, если дано уравнение директрисы х – 5 = 0.
; в) параболы, если дано уравнение директрисы х – 5 = 0.
19 вариант. Составить канонические уравнения: а) эллипса, фокусы которого расположены на оси абсцисс, симметрично относительно начала координат, если даны точка  и эксцентриситет
и эксцентриситет 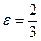 ; б) гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, кроме того, уравнения асимптот
; б) гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, кроме того, уравнения асимптот  и расстояние между вершинами равно 48; в) параболы, если уравнение ее директрисы y + 1 = 0.
и расстояние между вершинами равно 48; в) параболы, если уравнение ее директрисы y + 1 = 0.
20 вариант. Составить канонические уравнения: а) параболы, проходящей через начало координат и точку D (4, –8), расположенной симметрично относительно оси ординат; б) эллипса, фокусы которого расположены на оси абсцисс, симметрично относительно начала координат, если даны точка  принадлежащая эллипсу и расстояние между фокусами 2 с = 8; в) гиперболы, проходящей через точки А (2, 1) и В (
принадлежащая эллипсу и расстояние между фокусами 2 с = 8; в) гиперболы, проходящей через точки А (2, 1) и В (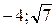 ).
).
21 вариант. Составить канонические уравнения: а) эллипса, проходящего через точки М 1(2; 3), М 2(0; 2); б) параболы, если ее фокус F (4; 0) и вершина совпадает с началом координат. в) Для гиперболы, заданной уравнением  найти длины полуосей, фокусы, уравнения асимптот.
найти длины полуосей, фокусы, уравнения асимптот.
22 вариант. а) Составить каноническое уравнение гиперболы, если она проходит через точку М(  ) и ее эксцентриситет
) и ее эксцентриситет 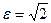 . б) Найти полуоси, фокусы и эксцентриситет эллипса
. б) Найти полуоси, фокусы и эксцентриситет эллипса  . в) Найти координаты фокуса и уравнение директрисы параболы y 2=12 x.
. в) Найти координаты фокуса и уравнение директрисы параболы y 2=12 x.
23 вариант. а) Найти координаты фокуса и уравнение директрисы параболы x 2 =8 y. б) Вычислить координаты фокусов и уравнения директрис гиперболы  ; в) Составить каноническое уравнение эллипса, проходящего через точки
; в) Составить каноническое уравнение эллипса, проходящего через точки  ,
, 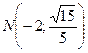 .
.
24 вариант. а) Определить длины полуосей и координаты фокусов эллипса x 2+3 y 2=6. б) Составить каноническое уравнение гиперболы, пересекающей ось Оу и проходящей через точки М( 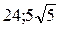 ), N (0, 5); в) Найти координаты фокуса и уравнения директрисы параболы
), N (0, 5); в) Найти координаты фокуса и уравнения директрисы параболы  .
.
25 вариант. а) Составить каноническое уравнение эллипса, полуоси которого равны, соответственно 3 и 6. б) Найти уравнение гиперболы, вершины и фокусы которой находятся в соответствующих вершинах и фокусах эллипса 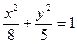 ; в) Найти координаты фокусов и уравнение директрисы параболы y 2=6 x.
; в) Найти координаты фокусов и уравнение директрисы параболы y 2=6 x.
26 вариант. а) Составить каноническое уравнение эллипса, если две его вершины находятся в точках А 1(8, 0) и А 2 (–8, 0), а фокусы – в вершинах F 1(5, 0) и F 2(–5, 0). б) Написать каноническое уравнение гиперболы, проходящей через точку (2, 1) и асимптоты которой 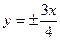 . в) Написать уравнение параболы с вершиной в начале координат, для которой директрисой служит прямая х = –2.
. в) Написать уравнение параболы с вершиной в начале координат, для которой директрисой служит прямая х = –2.
27 вариант. а) Дан эллипс 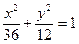 и точка на нем с абсциссой, равной 3. Найти ее ординату. б) Найти координаты фокусов гиперболы
и точка на нем с абсциссой, равной 3. Найти ее ординату. б) Найти координаты фокусов гиперболы 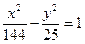 . в) Написать каноническое уравнение параболы с вершиной в начале координат и директрисой x = 3.
. в) Написать каноническое уравнение параболы с вершиной в начале координат и директрисой x = 3.
28 вариант. а) Написать каноническое уравнение гиперболы, если ее фокусы находятся в точках F 1(–4, 0) и F 2(4, 0) и длина действительной оси равна 6. б) Составить каноническое уравнение параболы с вершиной в начале координат и фокусом F (0, –5). в) Найти уравнение равносторонней гиперболы, проходящей через точку (3,–1).
29 вариант. а) Определить фокусы и полуоси эллипса 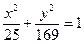 . б) Составить каноническое уравнение гиперболы, если действительная ось равна 16, а угол между асимптотой и осью абсцисс определяется условием
. б) Составить каноническое уравнение гиперболы, если действительная ось равна 16, а угол между асимптотой и осью абсцисс определяется условием 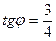 . в) Составить каноническое уравнение параболы, если расстояние от фокуса до вершины равно 3.
. в) Составить каноническое уравнение параболы, если расстояние от фокуса до вершины равно 3.
30 вариант. а) Составить каноническое уравнение эллипса, если большая полуось равна 26 и эксцентриситет 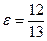 . б) Составить каноническое уравнение параболы, если расстояние от фокуса до директрисы равно 2. в) Определить полуоси, фокусы и асимптоты гиперболы
. б) Составить каноническое уравнение параболы, если расстояние от фокуса до директрисы равно 2. в) Определить полуоси, фокусы и асимптоты гиперболы 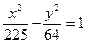 .
.
Задание 23. Привести к каноническому виду уравнение кривой второго порядка 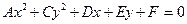 , определить тип линии и построить эту кривую.
, определить тип линии и построить эту кривую.
| № вар. | Коэффициенты уравнений кривой | № вар | Коэффициенты уравнений кривой | ||||||||
| A | C | D | E | F | A | C | D | E | F | ||
| –6 | –15 | –1 | –5 | ||||||||
| –1 | –54 | –32 | |||||||||
| –9 | –8 | –36 | –68 | –40 | |||||||
| –26 | –54 | –64 | –127 | –24 | |||||||
| –6 | –6 | –1 | |||||||||
| –28 | –12 | –8 | –6 | –24 | –36 | ||||||
| –8 | –19 | –4 | –1 | –4 | |||||||
| –4 | –36 | –8 | –4 | –12 | –3 | ||||||
| –30 | –4 | –72 | –88 | ||||||||
| –4 | –16 | –92 | |||||||||
| –2 | |||||||||||
| –2 | –42 | –16 | –4 | –72 | |||||||
| –1 | –4 | –4 | –4 | ||||||||
| –4 | –16 | –8 | |||||||||
| –4 | –36 | –8 | –4 | –100 | –44 |
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 1423; Нарушение авторских прав?; Мы поможем в написании вашей работы!