
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгебра и геометрия 6 страница
|
|
|
|
28. 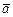 = (1, –3, 1),
= (1, –3, 1), 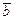 = (–2, –4, 3),
= (–2, –4, 3), 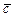 = (0, –2, 3),
= (0, –2, 3),  = (–8, –10, 13).
= (–8, –10, 13).
29. 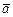 = (5, 7, –2),
= (5, 7, –2), 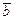 = (–3, 1, 3),
= (–3, 1, 3), 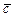 = (1, –4, 6),
= (1, –4, 6),  = (14, 9, –1).
= (14, 9, –1).
30. 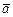 = (–1, 4, 3),
= (–1, 4, 3), 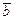 = (3, 2, –4),
= (3, 2, –4), 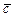 = (–2, –7, 1),
= (–2, –7, 1),  = (6, 20, –3).
= (6, 20, –3).
Задание 14. Записать общее уравнение и построить прямые, найти их угловые коэффициенты:
1) прямая задана точкой  и нормальным вектором
и нормальным вектором  ;
;
2) прямая задана точкой  и направляющим вектором
и направляющим вектором 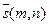 ;
;
3) прямая задана двумя точками  и
и  ;
;
4) прямая задана точкой  и угловым коэффициентом
и угловым коэффициентом 
| № | 
| 
| 
| 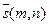
| 
| 
| 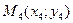
| 
|
| (1,2) | (–3,1) | (2,–1) | (3,–4) | (–5,0) | (2, –3) | (4,-1) | ||
| (2,–3) | (0,4) | (3,1) | (–2,5) | (0,–3) | (4,0) | (5,1) | –2 | |
| (3, 2) | (1, 1) | (8, 4) | (4, 5) | (6, 5) | (3, 2) | (6, 9) | ||
| (0, 6) | (7, 2) | (–2, 4) | (5, 7) | (4, 0) | (6, 8) | (2, 3) | –1 | |
| (2, 4) | (6, 4) | (5, 2) | (5, 5) | (1, 2) | (5, 7) | (8, 7) | ||
| (3, 2) | (4, 6) | (–2, –3) | (–3, 1) | (3, 0) | (0, 4) | (1, –1) | ||
| (–2, 1) | (5, 3) | (–1, 2) | (4, –1) | (7, 10) | (5, –4) | (1, –1) | –3 | |
| (4, 0) | (5, 6) | (1, 2,) | (3, 2) | (6, 9) | (4, 0) | (–2, 0) | ||
| (4, 10) | (3, 5) | (–2, –4) | (0, 4) | (–2, 5) | (3, 0) | (3, 2) | ||
| (6, 9) | (1, 2) | (1, –1) | (4, 5) | (3, 4) | (6, 6) | (6, 6) | ||
| (1,1) | (–1,4) | (2,6) | (–2,–1) | (3, 2) | (1, 3) | (–2, 2) | –3 | |
| (0, 5) | (2, 3) | (0, 0) | (–3, 1) | (1, 3) | (3, 2) | (4, 0) | –6 | |
| (0, 0) | (4, 0) | (1, 3) | (4, –1) | (3, 1) | (1, –2) | (2, 2) | –5 | |
| (2, –5) | (3, 2) | (5, –3) | (–5, 3) | (–2, 1) | (2, 2) | (3, 1) | ||
| (6, 0) | (0, 6) | (4, 6) | (0, –6) | (2, 2) | (–2, 1) | (1, –2) | ||
| (3, 2) | (2, 4) | (4, 3) | (–2, 4) | (1, –1) | (5, –2) | (–1, 3) | –4 | |
| (6, 3) | (5, –4) | (3, 5) | (–6, 2) | (6, 15) | (3, 0) | (4, 5) | ||
| (5, –2) | (4, 0) | (2, 5) | (1, 2) | (1, –2) | (1, –2) | (2, 2) | –5 | |
| (4, 2) | (3, 0) | (0, 3) | (5, –2) | (4, 0) | (1, 2) | (1, 3) | –5 | |
| (4, 2) | (3, 0) | (0, 2) | (5, –2) | (–5, 6) | (–5, 2) | (6, 5) | ||
| (4, 4) | (7, 10) | (2, 8) | (9, 6) | (6, 6) | (8, 4) | (8, 9) | –4 | |
| (4, 6) | (6, 9) | (2, 10) | (7, 5) | (8, 2) | (2, 6) | (7, 4) | –3 | |
| (3, 5) | (8, 7) | (5, 10) | (4, 7) | (6, 5) | (9, 5) | (6, 11) | ||
| (10, 6) | (–2, 8) | (6, 8) | (7, 10) | (2, 2) | (7, 7) | (3, 1) | –2 | |
| (1, 8) | (5, 2) | (5, 7) | (4, 10) | (6, 4) | (5, 5) | (6, 8) | –3 | |
| (6, 6) | (4, 9) | (4, 6) | (6, 9) | (7, 3) | (5, 8) | (5, 8) | –6 | |
| (7, 2) | (5, 7) | (5, 3) | (2, 3) | (1, 2) | (0, 0) | (2, 7) | ||
| (8, 6) | (10, 5) | (5, 6) | (8, 10) | (2, 7) | (3, 2) | (1, 2) | –1 | |
| (7, 7) | (6, 5) | (3, 5) | (8, 4) | (3, 2) | (2, 7) | (0, 0) | ||
| (–2, 1) | (4, 0) | (3, 2) | (1, 3) | (1, –2) | (–2, 1) | (2, 5) |
Задание 15. Даны вершины треугольника  :
:  ,
,  ,
,  . Построить треугольник и найти:
. Построить треугольник и найти:
1.) уравнения сторон  и
и 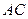 ;
;
2.) уравнение высоты 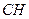 ;
;
3.) уравнение медианы  ;
;
4.) точку 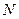 пересечения медианы
пересечения медианы  и высоты
и высоты 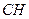 ;
;
5.) уравнение прямой, проходящей через вершину  параллельно стороне
параллельно стороне  ;
;
6.) угол  ;
;
7.) длину высоты 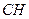 .
.
| № вар. | 
| 
| 
| № вар. | 
| 
| 
|
| (–2;4) | (3;1) | (10;7) | (–3; –2) | (14;4) | (6;8) | ||
| (1;7) | (–3; –1) | (11; –3) | (1;0) | (–1;4) | (9;5) | ||
| (1; –2) | (7;1) | (3;7) | (–2; –3) | (1;6) | (6;1) | ||
| (–4;2) | (–6;6) | (6;2) | (4; –3) | (7;3) | (1;10) | ||
| (4; –4) | (8;2) | (3;8) | (–3; –3) | (5; –7) | (7;7) | ||
| (1; –6) | (3;4) | (–3;3) | (–4;2) | (8; –6) | (2;6) | ||
| (–5;2) | (0; –4) | (5;7) | (4; –4) | (6;2) | (–1;8) | ||
| (–3;8) | (–6;2) | (0; –5) | (6; –9) | (10; –1) | (–4;1) | ||
| (4;1) | (–3; –1) | (7; –3) | (–4;2) | (6; –4) | (4;10) | ||
| (3; –1) | (11;3) | (–6;2) | (–7; –2) | (–7;4) | (5; –5) | ||
| (–1; –4) | (9;6) | (–5;4) | (10; –2) | (4; –5) | (–3;1) | ||
| (–3; –1) | (–4; –5) | (8;1) | (–2; –6) | (–3;5) | (4;0) | ||
| (–7; –2) | (3; –8) | (–4;6) | (0;2) | (–7; –4) | (3;2) | ||
| (7;0) | (1;4) | (–8; –4) | (1; –3) | (0;7) | (–2;4) | ||
| (–5;1) | (8; –2) | (1;4) | (2;5) | (–3;1) | (0;4) |
Задание 16. Решить следующие задачи.
1 вариант. Найти уравнение прямой, проходящей через точку пересечения прямых  и
и 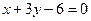 отсекающей на оси абсцисс отрезок, равный 3.
отсекающей на оси абсцисс отрезок, равный 3.
2 вариант. Найти проекцию точки А (–8,12) на прямую, проходящую через точки В (2,–3) и С (–5,1).
3 вариант. Даны две вершины треугольника ABC: A (–4,4), В (4, –12) и точка М (4,2) пересечения его высот. Найти вершину С.
4 вариант. Найти уравнение прямой, отсекающей на оси ординат отрезок, равный 2, и проходящей параллельно прямой 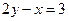
5 вариант. Найти уравнение прямой, проходящей через точку А (2, –3) и точку пересечения прямых  и
и 
6 вариант. Доказать, что четырехугольник A B C D – трапеция, если А (3, 6), В (5, 2), С (–1,–3), D (–5,5).
7 вариант. Записать уравнение прямой, проходящей через точку А (3,1) перпендикулярно к прямой ВС, если В (2,5), С (1,0).
8 вариант. Найти уравнение прямой, проходящей через точку А (–2,1) параллельно прямой MN, если М (–3, –2), N (1,6).
9 вариант. Найти точку, симметричную точке М (2,–1) относительно прямой  .
.
10 вариант. Найти точку О пересечения диагоналей четырехугольника ABCD, если А (–1, –3), В (3,5), С (5,2), D (3, –5).
11 вариант. Через точку пересечения прямых  ,
,  провести прямую, параллельную оси абсцисс.
провести прямую, параллельную оси абсцисс.
12 вариант. Известны уравнения стороны АВ треугольника ABC  , его высот ВН
, его высот ВН  АМ
АМ 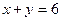 . Найти уравнения двух других сторон треугольника ABC.
. Найти уравнения двух других сторон треугольника ABC.
13 вариант. Даны две вершины треугольника ABC A (–6,2), В (2,– 2) и точка пересечения его высот H (1,2). Найти координаты точки М пересечения стороны АС и высоты ВН.
14 вариант. Найти уравнения высот треугольника ABC, проходящих через вершины А и В, если А (– 4, 2), B (3, –5), С (5,0).
15 вариант. Вычислить координаты точки пересечения перпендикуляров, проведенных через середины сторон треугольника, вершинами которого служат точки А (2,3), В (0, –3), С (6, –3).
16 вариант. Составить уравнение высоты, проведенной через вершину А треугольника ABC, зная уравнения его сторон:  (АВ),
(АВ),  (АС),
(АС),  (ВС).
(ВС).
17 вариант. Дан треугольник с вершинами А (3,1), В (–3, –1) и С (5,–12). Найти уравнение медианы, проведенной из вершины С, и вычислить ее длину.
18 вариант. Составить уравнение прямой, проходящей через начало координат и точку пересечения прямых 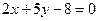 и
и 
19 вариант. Найти уравнения перпендикуляров к прямой 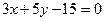 , проведенных через точки пересечения данной прямой с осями координат.
, проведенных через точки пересечения данной прямой с осями координат.
20 вариант. Даны уравнения сторон четырехугольника:  ,
,  ,
,  ,
, 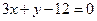 .Найти уравнения его диагоналей.
.Найти уравнения его диагоналей.
21 вариант. Составить, уравнения медианы СМ и высоты СК треугольника ABC, если А (4,6), В (–4,0), С (–1,–4).
22 вариант. Через точку Р (5, 2)провести прямую: а) отсекающую равные отрезки на осях координат; б) параллельную оси Ох;в) параллельную оси Оу.
23 вариант. Записать уравнение прямой, проходящей через точку А (–2,3)и составляющей с осью Ох угол: а) 45°; б) 90°; в) 0°.
24 вариант. Какую ординату имеет точка С, лежащая на одной прямой с точками А (–6,–6) и В (–3, –1) и имеющая абсциссу, равную 3?
25 вариант. Через точку пересечения прямых  и
и 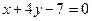 провести прямую, делящую отрезок между точками А (4 –3)и В (–1,2) в отношении
провести прямую, делящую отрезок между точками А (4 –3)и В (–1,2) в отношении  =2/3.
=2/3.
26 вариант. Известны уравнения двух сторон ромба  и
и  и уравнение одной из его диагоналей
и уравнение одной из его диагоналей 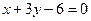 . Найти уравнение второй диагонали.
. Найти уравнение второй диагонали.
27 вариант. Найти точку Е пересечения медиан треугольника, вершинами которого являются точки А (–3,1), В (7,5) и С (5, –3).
28 вариант. Записать уравнения прямых, проходящих через точку А (–1,1)под углом 45° к прямой  .
.
29 вариант. Даны уравнения высот треугольника ABC  ,
,  и координаты его вершины А (2,3). Найти уравнения сторон АВ и АС треугольника.
и координаты его вершины А (2,3). Найти уравнения сторон АВ и АС треугольника.
30 вариант. Даны уравнения двух сторон параллелограмма  ,
,  и точка пересечения его диагоналей М (3,–1). Найти уравнения двух других сторон.
и точка пересечения его диагоналей М (3,–1). Найти уравнения двух других сторон.
Задание 17. Написать общее уравнение и построить плоскости заданные следующим образом:
1) точкой  и нормальным вектором
и нормальным вектором  ;
;
2) отрезками 
 и
и  , отсекаемыми данной плоскостью на осях координат
, отсекаемыми данной плоскостью на осях координат 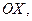
 и
и  соответственно;
соответственно;
3) тремя точками  ,
,  и
и  ;
;
4) двумя точками  и
и  и направляющим (параллельным) вектором
и направляющим (параллельным) вектором 
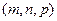 ;
;
5) найти косинус угла между плоскостями из п.1) и 2);
6) найти расстояние от точки 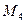 до плоскости из п. 3).
до плоскости из п. 3).
1 вариант. 1)  , ,  ;
2) ;
2) 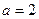 , , 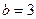 , ,  ;
3) ;
3) 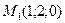 , ,  , ,  ;
4) ;
4)  , ,  , , 
| 2 вариант. 1)  , ,  ;
2) ;
2)  , ,  , , 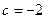 ;
3) ;
3)  , ,  , ,  ;
4) ;
4)  , ,  , , 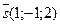
|
3 вариант. 1)  , ,  ;
2) ;
2)  , ,  , ,  ;
3) ;
3)  , ,  , ,  ;
4) ;
4) 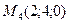 , ,  , , 
| 4 вариант. 1)  , ,  ;
2) ;
2) 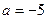 , ,  , ,  ;
3) ;
3)  , , 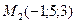 , ,  ;
4) ;
4)  , , 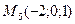 , , 
|
5 вариант. 1) 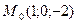 , ,  ;
2) ;
2)  2, 2,  4, 4,  –1;
3) –1;
3)  , ,  , ,  ;
4) ;
4)  , , 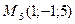 , , 
| 6 вариант. 1)  , ,  ;
2) ;
2)  –3, –3,  5, 5,  1;
3) 1;
3)  , ,  , , 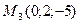 ;
4) ;
4)  , ,  , , 
|
7 вариант. 1)  , ,  ;
2) ;
2)  4, 4,  –3, –3,  1;
3) 1;
3)  , ,  , ,  ;
4) ;
4)  , ,  , , 
| 8 вариант. 1)  , ,  ;
2) ;
2)  –5, –5,  2, 2,  4;
3) 4;
3)  , ,  , ,  ;
4) ;
4)  , ,  , , 
|
9 вариант. 1) 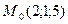 , ,  ;
2) ;
2)  3, 3,  4, 4,  –1;
3) –1;
3)  , ,  , ,  ;
4) ;
4)  , , 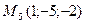 , , 
| 10 вариант. 1)  , ,  ;
2) ;
2)  1, 1,  4, 4,  –2;
3) –2;
3)  , ,  , ,  ;
4) ;
4)  , ,  , , 
|
11 вариант. 1)  , ,  ;
2) ;
2)  4, 4,  –3, –3,  5;
3) 5;
3)  , ,  , ,  ;
4) ;
4)  , ,  , , 
| 12 вариант. 1)  , ,  ;
2) ;
2)  3, 3,  1, 1,  –4;
3) –4;
3) 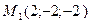 , ,  , ,  ;
4) ;
4)  , , 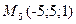 , , 
|
13 вариант. 1)  , ,  ;
2) ;
2)  3, 3,  –2, –2,  1;
3) 1;
3) 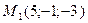 , , 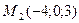 , ,  4)
4)  , , 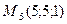 , , 
| 14 вариант. 1)  , , 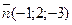 ;
2) ;
2)  –2, –2,  –1, –1,  4;
3) 4;
3)  , ,  , ,  ;
4) ;
4) 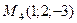 , , 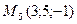 , , 
|
15 вариант. 1)  , ,  ;
2) ;
2)  4, 4,  –5, –5,  –3;
3) –3;
3)  , ,  , ,  ;
4) ;
4)  , ,  , , 
| 16 вариант. 1)  , ,  ;
2) ;
2)  –5, –5,  3, 3,  1;
3) 1;
3) 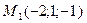 , ,  , ,  ;
4) ;
4)  , ,  , , 
|
17 вариант. 1)  , ,  ;
2) ;
2)  4, 4,  5, 5,  1;
3) 1;
3)  , ,  , ,  ;
4) ;
4)  , , 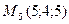 , , 
| 18 вариант. 1)  , ,  ;
2) ;
2)  –2, –2,  4, 4,  –3;
3) –3;
3)  , ,  , ,  ;
4) ;
4)  , ,  , , 
|
19 вариант. 1)  , , 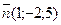 ;
2) ;
2)  2, 2,  –1, –1,  5;
3) 5;
3) 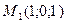 , ,  , ,  ;
4) ;
4)  , ,  , , 
| 20 вариант. 1)  , ,  ;
2) ;
2)  –3, –3,  5, 5,  2;
3) 2;
3)  , ,  , , 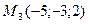 ;
4) ;
4)  , ,  , , 
|
21 вариант. 1)  , , 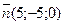 ;
2) ;
2)  –4, –4,  4, 4,  3;
3) 3;
3)  , ,  , ,  ;
4) ;
4)  , ,  , , 
| 22 вариант. 1) 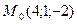 , ,  ;
2) ;
2)  2, 2,  –4, –4,  1;
3) 1;
3) 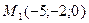 , ,  , ,  ;
4) ;
4) 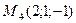 , , 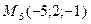 , , 
|
23 вариант. 1)  , ,  ;
2) ;
2)  –1, –1,  5, 5,  –3;
3) –3;
3)  , ,  , ,  ;
4) ;
4)  , ,  , , 
| 24 вариант. 1) 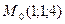 , ,  ;
2) ;
2)  –2, –2,  4, 4,  1;
3) 1;
3)  , ,  , ,  ;
4) ;
4)  , ,  , , 
|
25 вариант. 1)  , ,  ;
2) ;
2)  4, 4,  2, 2,  1;
3) 1;
3)  , ,  , ,  ;
4) ;
4)  , ,  , , 
| 26 вариант. 1)  , ,  ;
2) ;
2)  3, 3,  4, 4,  –3;
3) –3;
3)  , ,  , ,  ;
4) ;
4)  , ,  , , 
|
27 вариант. 1)  , ,  ;
2) ;
2)  5, 5,  –1, –1,  2;
3) 2;
3)  , ,  , ,  ;
4) ;
4)  , , 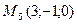 , , 
| 28 вариант. 1)  , ,  ;
2) ;
2)  –2, –2,  4, 4,  1;
3) 1;
3)  , ,  , ,  ;
4) ;
4)  , ,  , , 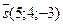
|
29 вариант. 1)  , , 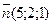 ;
2) ;
2)  2, 2,  3, 3,  4;
3) 4;
3)  , , 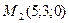 , ,  ;
4) ;
4)  , ,  , , 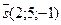
| 30 вариант. 1)  , ,  ;
2) ;
2)  –4, –4,  3, 3,  1;
3) 1;
3)  , ,  , ,  ;
4) ;
4)  , ,  , , 
|
Задание 18. Даны 4-е точки  ,
,  ,
,  и
и 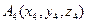 . Составить уравнения:
. Составить уравнения:
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 754; Нарушение авторских прав?; Мы поможем в написании вашей работы!