
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Краткие методические указания к решению задачи 2
|
|
|
|
Расчет показателей по индивидуальным данным проводится по каждому признаку – Х1, Х2, Х3 и Х4 в следующей последовательности:
1. Определяются итоговые обобщающие показатели, т. е. производится расчет сумм для каждого из признаков в отдельности
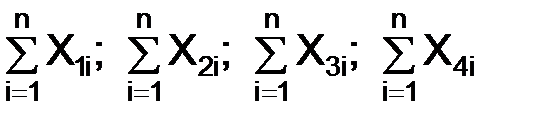 , (1)
, (1)
где i = 1…n; n – число единиц наблюдения.
2. Рассчитываются простые средние арифметические величины
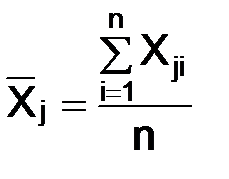 , (2)
, (2)
где j = 1…; m – число признаков; 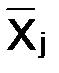 – простая среднеарифметическая величина j-го признака;
– простая среднеарифметическая величина j-го признака;  – индивидуальные значения j-го признака i-й единицы наблюдения.
– индивидуальные значения j-го признака i-й единицы наблюдения.
3. Рассчитываются показатели размаха вариации
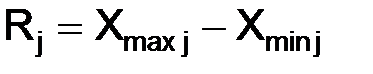 , (3)
, (3)
где 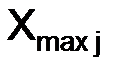 – максимальное значение j-го признака;
– максимальное значение j-го признака;  – минимальное значение j-го признака.
– минимальное значение j-го признака.
4. Рассчитываются средние линейные отклонения
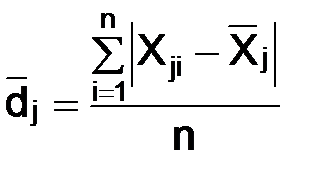 . (4)
. (4)
5. Рассчитываются дисперсии
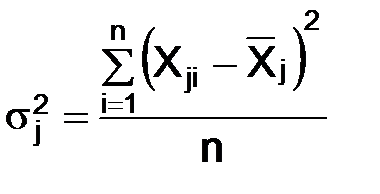 . (5)
. (5)
6. Рассчитайте среднеквадратические отклонения
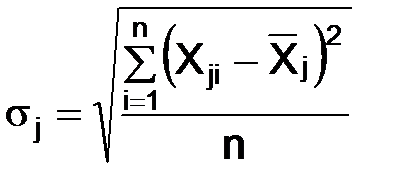 , (6)
, (6)
где i = 1…n, j = 1…m.
7. Определяются в относительных величинах коэффициенты вариации
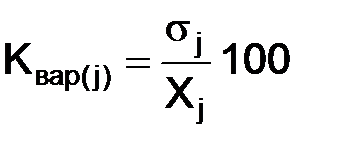 . (7)
. (7)
При проведении расчетов по вышеприведенным формулам целесообразно использовать вспомогательные расчеты таблицы, в которых представляется последовательность арифметических действий и все промежуточные результаты.
Например, при расчете средних величин, средних линейных отклонений и дисперсий для каждого признака (по условиям задачи) промежуточные таблицы могут быть представлены следующим образом:
| Номер п/п | Х (1) |  (2) (2)
|  (3) (3)
|  (4) (4)
|
| … | ||||
| N | ||||
| Итого | 
| 
| 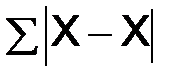
| 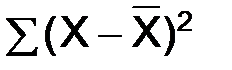
|
Полученные в результате расчетов обобщающие статистические характеристики оформляются в виде выходных статистических таблиц.
Ниже для иллюстрации нами приводятся результаты расчетов этих характеристик отдельно для количественных признаков – Х1, Х2, и Х3 (непрерывные признаки – Х1 и Х2 и дискретный признак Х3) и для альтернативного признака Х4, выполненные по данным информационной таблицы базового варианта (табл. 1).
Основные статистические характеристики количественных признаков – Х1, Х2, Х3 представлены в табл. 3.
Таблица 3
| номер п/п | Показатели | Х1, руб. | Х2, руб. | Х3, руб. |
| Итоговые обобщающие показатели | ||||
| Средние величины | 7465,83 | 3663,00 | 3,73 | |
| Размах вариации | ||||
| Средние линейные отклонения | 1732,2 | 747,87 | 0,93 | |
| Дисперсии | 4403140,14 | 834847,67 | 1,26 | |
| Средние квадратические отклонения | 2098,37 | 913,70 | 1,12 | |
| Коэффициент вариаций, % | 28,11 | 24,94 | 30,09 |
Основные статистические характеристики альтернативного признака – Х4 (табл. 4).
Таблица 4
| номер п/п | Показатели | Х4 |
Сумма единиц, обладающая данным признаком 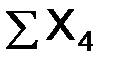
| ||
Доля единиц, обладающая данным признаком 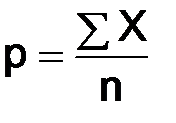
| 0,50 | |
| Доля единиц, не обладающая данным признаком = (1 – p) | 0,50 | |
Дисперсия альтернативного признака 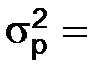 pq pq
| 0,25 | |
Среднеквадратическое отклонение альтернативного признака  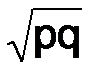
| 0,25 |
Представленные выходные таблицы в этой и всех последующих задачах носят рекомендательный характер, так как возможны и другие формы представления данных.
В целях упрощения нумерация формул, таблиц, графиков дается по каждой задаче в отдельности.
Задача 3
По данным информационной таблицы вашего варианта произведите группировку индивидуальных данных, приняв за основу группировки количественный непрерывный признак Х1. Группы образуйте с равными и неравными интервалами в следующей последовательности.
1. Образуйте группы с равными интервалами. По каждой группе определите:
а) число единиц наблюдения в абсолютных и относительных величинах (процент к итогу);
б) групповые обозначающие итоговые показатели признаков – Х1, Х2, Х3, Х4 в абсолютных и относительных величинах (процент к итогу);
в) групповые средние величины и групповые частные дисперсии признаков – Х1, Х2, Х3, Х4.
2. Образуйте группы с неравными (равнонаправленными) интервалами – 10 групп по 10 % единиц наблюдения в каждом интервале и 5 групп по
20 % единиц наблюдения также в каждом интервале. По каждой группе для признаков Х1, Х2, Х3, Х4 (для названных вариантов) рассчитайте групповые итоговые значения названных признаков в абсолютных и относительных величинах (процент к итогу).
3. Образуйте 5 групп с интервалами, меняющимися по правилу арифметической прогрессии. Рассчитайте абсолютные и относительные показатели плотности распределения. Все полученные результаты (пункты 1, 2, 3) представьте в статистических таблицах.
|
|
|
|
|
Дата добавления: 2014-12-23; Просмотров: 421; Нарушение авторских прав?; Мы поможем в написании вашей работы!