
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Асимметричные криптосистемы 2 страница. Иногда рекомендуется выбирать открытый ключ одинаковым для всех абонентов сети, например =3
|
|
|
|
Иногда рекомендуется выбирать открытый ключ 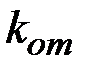 одинаковым для всех абонентов сети, например
одинаковым для всех абонентов сети, например 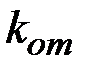 =3. Это обеспечивает увеличение скорости шифрования.
=3. Это обеспечивает увеличение скорости шифрования.
Рассмотренная криптосистема обладает одним существенным недостатком. Рассмотрим схему на рис.1.1. Злоумышленник, под видом абонента 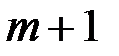 , либо самостоятельно инициирует обмен информацией между абонентами
, либо самостоятельно инициирует обмен информацией между абонентами 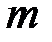 и
и 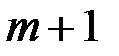 , либо «встраивается» между абонентами в процессе обмена ими информацией. Абонент
, либо «встраивается» между абонентами в процессе обмена ими информацией. Абонент 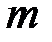 шифрует сообщение для передачи его абоненту
шифрует сообщение для передачи его абоненту 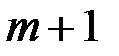 используя при этом «подставленные» злоумышленником параметры
используя при этом «подставленные» злоумышленником параметры 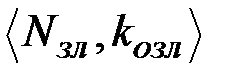 . Перехваченная криптограмма
. Перехваченная криптограмма 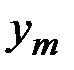 расшифровывается злоумышленником с помощью его закрытого ключа
расшифровывается злоумышленником с помощью его закрытого ключа 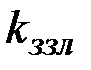 . Полученный открытый текст
. Полученный открытый текст 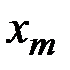 злоумышленник снова зашифровывает используя параметры
злоумышленник снова зашифровывает используя параметры 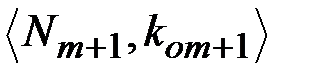 абонента
абонента 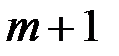 . Абонент
. Абонент 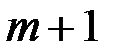 расшифровывает полученную криптограмму, используя закрытый ключ
расшифровывает полученную криптограмму, используя закрытый ключ 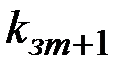 . Затем абонент
. Затем абонент 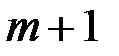 формирует ответное сообщение, которое аналогично перехватывается злоумышленником. Таким образом, злоумышленник, находясь «посередине» между абонентами читает передаваемые ими сообщения. Избежать такой ситуации можно за счет использования более сложных протоколов, например следующего.
формирует ответное сообщение, которое аналогично перехватывается злоумышленником. Таким образом, злоумышленник, находясь «посередине» между абонентами читает передаваемые ими сообщения. Избежать такой ситуации можно за счет использования более сложных протоколов, например следующего.
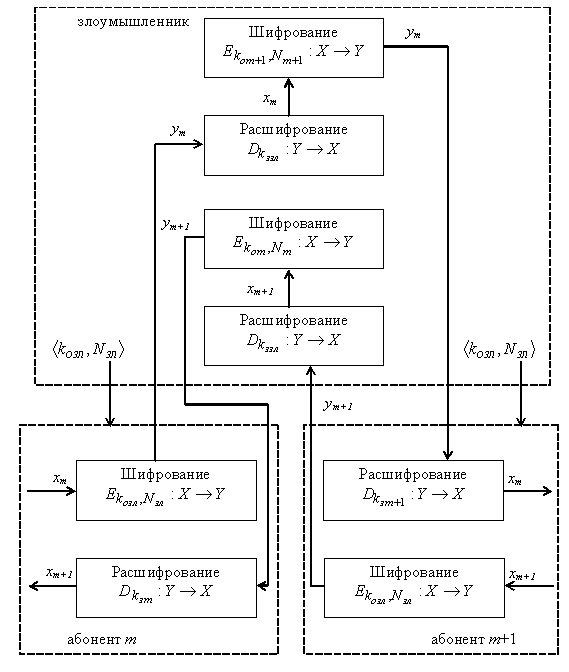
Рис. 1.1. Схема «активный злоумышленник посередине»
Пусть абонент 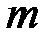 хочет передать сообщение абоненту
хочет передать сообщение абоненту 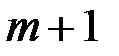 . Сначала абонент
. Сначала абонент 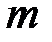 вычисляет:
вычисляет:
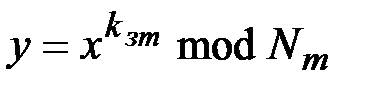 .
.
Затем абонент 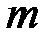 вычисляет
вычисляет
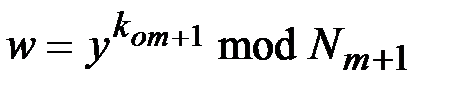 ,
,
и передает его абоненту 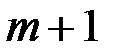 . Абонент
. Абонент 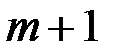 получив криптограмму последовательно вычисляет
получив криптограмму последовательно вычисляет
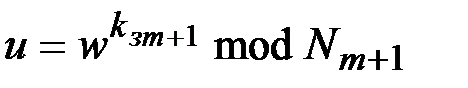 и
и  .
.
При таком протоколе злоумышленник уже не может реализовать схему перехвата сообщений, представленную на рис.1.1.
Рассмотрим пример шифрования при помощи алгоритма криптосистемы RSA. Пусть открытое сообщение, подлежащее шифрованию 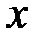 =15. Сеть состоит из двух абонентов. Параметры второго абонента, которому адресуется шифрованное сообщение следующие:
=15. Сеть состоит из двух абонентов. Параметры второго абонента, которому адресуется шифрованное сообщение следующие: 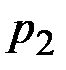 =3,
=3, 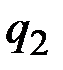 =11,
=11, 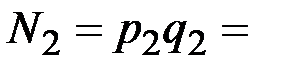 33,
33, 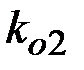 =3 (число 3 взаимно простое с
=3 (число 3 взаимно простое с 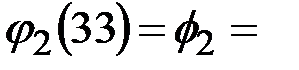 20). Закрытый ключ, определенный с помощью алгоритма Евклида
20). Закрытый ключ, определенный с помощью алгоритма Евклида 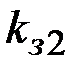 =7 (
=7 (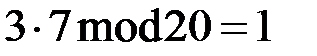 ). Шифруем открытый текст:
). Шифруем открытый текст:
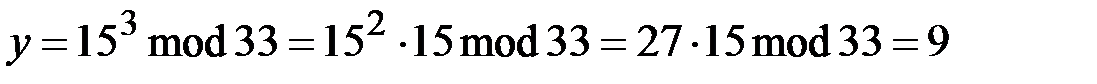 .
.
Расшифруем сообщение:
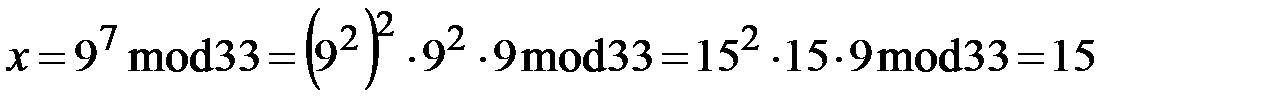 .
.
1.4. Криптосистема Шамира
Криптосистема, предложенная Ади Шамиром, была первой криптосистемой с открытым ключом.
Определение 1.9. Криптосистема Шамира формально определяется следующим образом [6-9]:
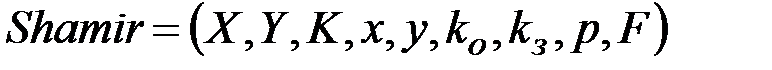 , (1.15)
, (1.15)
где 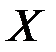 - множество открытых текстов,
- множество открытых текстов, 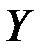 - множество криптограмм,
- множество криптограмм, 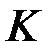 - множество ключей,
- множество ключей, 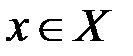 - некоторый открытый текст,
- некоторый открытый текст, 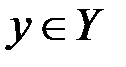 - некоторая криптограмма,
- некоторая криптограмма, 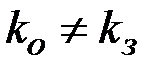 ,
, 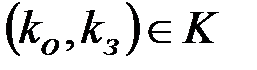 - ключи шифрования, удовлетворяющие условию
- ключи шифрования, удовлетворяющие условию 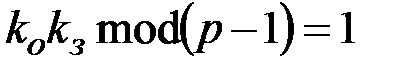 ,
, 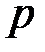 - большое простое число,
- большое простое число, 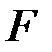 - криптографическая функция.
- криптографическая функция.
Пусть два абонента сети 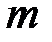 и
и 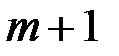 ,
, 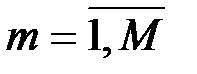 , собираются обменяться шифрованными сообщениями, используя открытый канал связи. Абонент
, собираются обменяться шифрованными сообщениями, используя открытый канал связи. Абонент 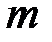 выбирает большое простое число
выбирает большое простое число 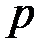 и передает его абоненту
и передает его абоненту 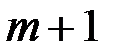 , а затем выбирает два числа
, а затем выбирает два числа 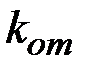 и
и 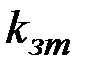 , такие что
, такие что
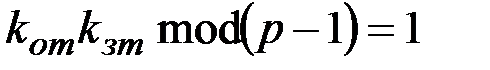 .
.
Эти числа абонент 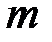 держит в секрете и передавать не будет. Абонент
держит в секрете и передавать не будет. Абонент 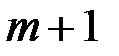 тоже выбирает два числа
тоже выбирает два числа 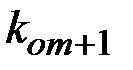 и
и  , такие что
, такие что
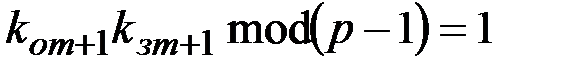 .
.
и держит их в секрете.
После этого абонент 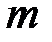 передает сообщение, используя трехступенчатый протокол. При передаче сообщения проверяется условие
передает сообщение, используя трехступенчатый протокол. При передаче сообщения проверяется условие 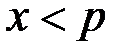 . Если условие
. Если условие 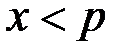 выполняется, то сообщение сразу зашифровывается и передается по каналу связи. Если условие
выполняется, то сообщение сразу зашифровывается и передается по каналу связи. Если условие 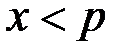 не выполняется, то сообщение представляется в виде блоков
не выполняется, то сообщение представляется в виде блоков 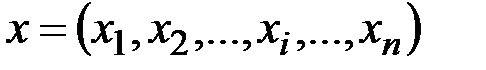 , причем
, причем 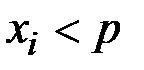 . Затем каждый блок зашифровывается и передается по каналу связи. Для обеспечения криптостойкости абоненты выбираю для каждого
. Затем каждый блок зашифровывается и передается по каналу связи. Для обеспечения криптостойкости абоненты выбираю для каждого 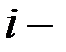 го блока свою пару
го блока свою пару 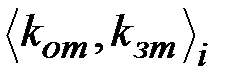 и
и 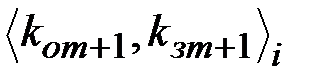 .
.
Дадим описание трехступенчатого протокола (см. рис. 1.2.). Абонент 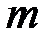 вычисляет число
вычисляет число
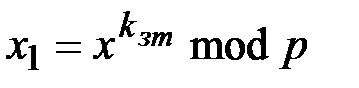 .
.
Абонент 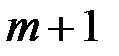 , получив
, получив 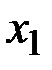 , вычисляет
, вычисляет
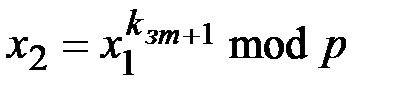
и передает его абоненту 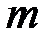 . Абонент
. Абонент 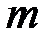 вычисляет следующее число
вычисляет следующее число
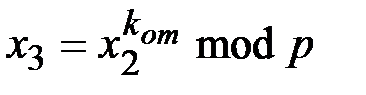
и передает его абоненту 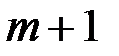 . Абонент
. Абонент 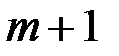 , получив
, получив 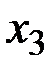 , вычисляет
, вычисляет
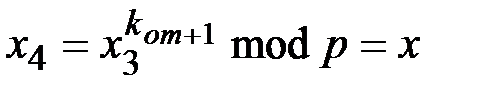 ,
,
которое является передаваемым исходным сообщением.
□ Для доказательства корректности протокола заметим, что любое целое число 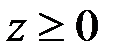 может быть представлено в виде
может быть представлено в виде
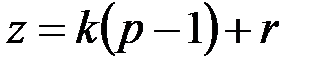 , где
, где 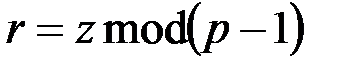 .
.
На основании теоремы 1.4 (теорема Ферма) можно записать
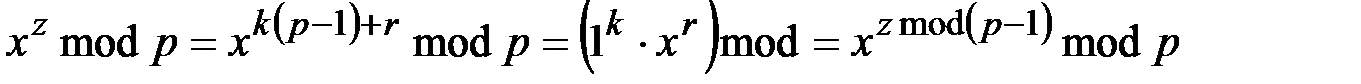 .
.
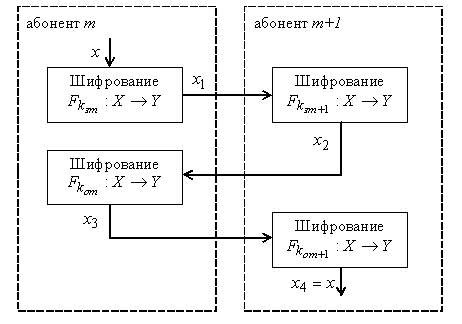
Рис. 1.2. Схема алгоритма Шамира
Тогда
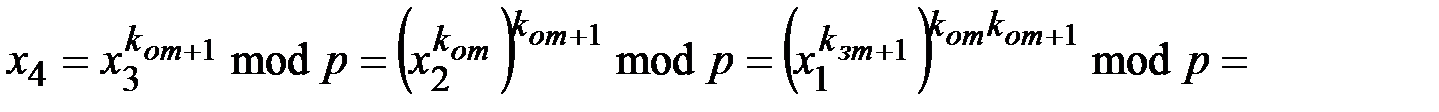
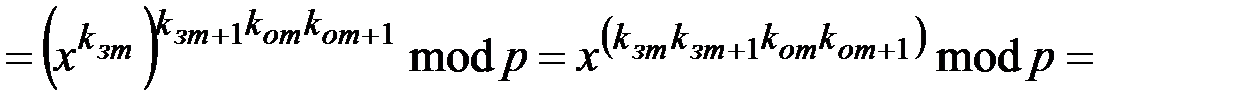
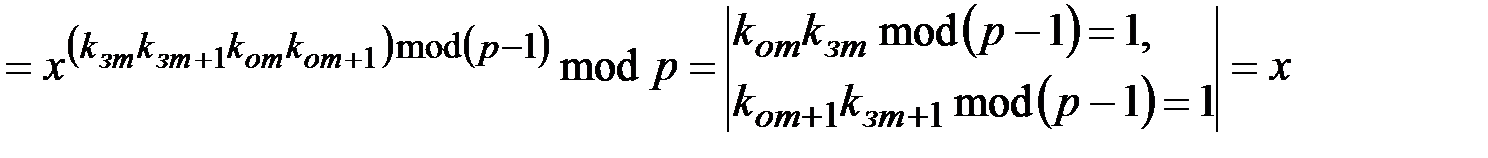 . ■
. ■
Злоумышленник не может прочесть переданное сообщение. Действительно, злоумышленник, перехватывая передаваемые сообщения 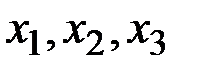 должен решать задачу дискретного логарифмирования, что при больших
должен решать задачу дискретного логарифмирования, что при больших 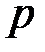 невозможно.
невозможно.
Рассмотрим пример шифрования при помощи алгоритма Шамира. Пусть открытое сообщение, подлежащее шифрованию 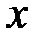 =10. Сеть состоит из двух абонентов. Первый абонент выбирает
=10. Сеть состоит из двух абонентов. Первый абонент выбирает 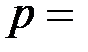 23, и параметры
23, и параметры 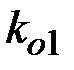 =19,
=19, 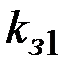 =7 (
=7 (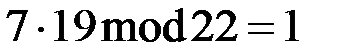 ). Аналогично второй абонент выбирает параметры
). Аналогично второй абонент выбирает параметры 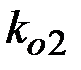 =9,
=9, 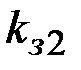 =5 (
=5 (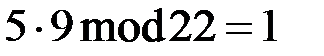 ). Протокол Шамира:
). Протокол Шамира:
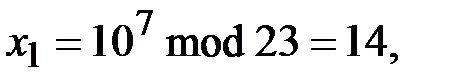 .
.
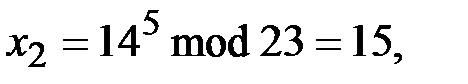
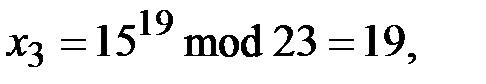
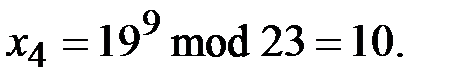
Очевидный недостаток криптосистемы Шамира заключается в необходимости реализации трехступенчатого протокола. Это влечет за собой увеличение времени на передачу сообщения, а также увеличивает вероятность искажения принятого сообщения из-за помех в канале передачи информации.
1.5. Криптосистема Эль Гамаля
Определение 1.10. Криптосистема с открытым ключом Эль Гамаля формально определяется следующим образом [6-9]:
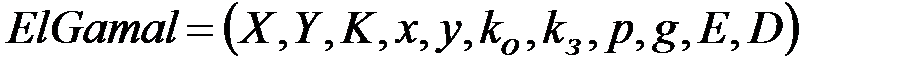 , (1.16)
, (1.16)
где 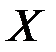 - множество открытых текстов,
- множество открытых текстов, 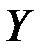 - множество криптограмм,
- множество криптограмм, 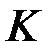 - множество ключей,
- множество ключей, 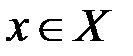 - некоторый открытый текст,
- некоторый открытый текст, 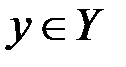 - некоторая криптограмма,
- некоторая криптограмма, 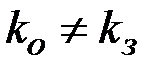 ,
, 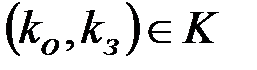 - ключи шифрования и расшифрования, удовлетворяющие условию:
- ключи шифрования и расшифрования, удовлетворяющие условию: 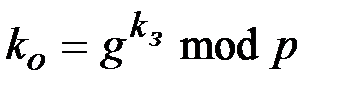 ,
, 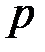 - большое простое число,
- большое простое число, 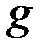 - число, такое что, различные степени числа
- число, такое что, различные степени числа 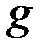 суть различные числа по модулю
суть различные числа по модулю 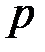 ,
, 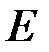 - функция шифрования,
- функция шифрования, 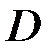 - функция расшифрования.
- функция расшифрования.
Для всей группы 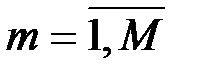 абонентов сети выбирается некоторое большое простое число
абонентов сети выбирается некоторое большое простое число 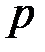 и число
и число 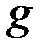 . Выбор числа
. Выбор числа 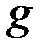 может оказаться трудной задачей при произвольно заданном числе
может оказаться трудной задачей при произвольно заданном числе 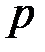 , т.к. это связано с разложением на простые множители числа
, т.к. это связано с разложением на простые множители числа 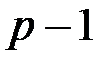 . Дело в том, что для обеспечения высокой стойкости алгоритма шифрования число
. Дело в том, что для обеспечения высокой стойкости алгоритма шифрования число 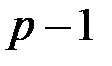 должно обязательно содержать большой простой множитель, в противном случае с помощью алгоритма Полига-Хеллмана быстро вычисляется дискретный логарифм. В связи с этим простое число
должно обязательно содержать большой простой множитель, в противном случае с помощью алгоритма Полига-Хеллмана быстро вычисляется дискретный логарифм. В связи с этим простое число 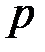 выбирается таким, чтобы выполнялось равенство
выбирается таким, чтобы выполнялось равенство
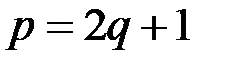 , (1.17)
, (1.17)
где 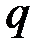 - простое число. Тогда в качестве
- простое число. Тогда в качестве 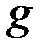 можно взять любое число, для которого справедливы неравенства
можно взять любое число, для которого справедливы неравенства
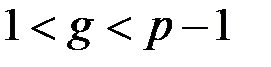 ,
, 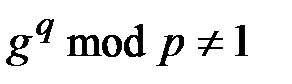 . (1.18)
. (1.18)
Числа 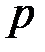 и
и 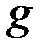 передаются абонентам сети в открытом виде. Затем каждый абонент сети выбирает секретный ключ
передаются абонентам сети в открытом виде. Затем каждый абонент сети выбирает секретный ключ 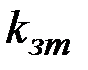 ,
, 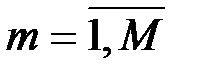 , удовлетворяющее условию:
, удовлетворяющее условию: 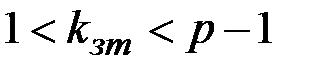 , и вычисляет открытый ключ:
, и вычисляет открытый ключ:
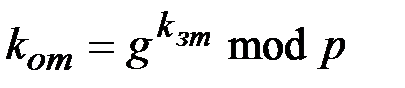 ,
, 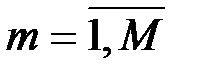 . (1.19)
. (1.19)
Пусть абонент 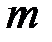 хочет передать абоненту
хочет передать абоненту 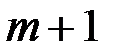 сообщение
сообщение 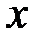 , при этом необходимо выполнение условия:
, при этом необходимо выполнение условия: 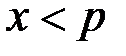 .
.
Шифрование исходного сообщения 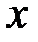 происходит следующим образом. Абонент
происходит следующим образом. Абонент 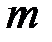 формирует случайное число
формирует случайное число 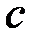 , причем
, причем 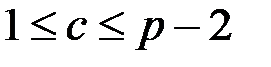 (эту операцию выполняют все абоненты сети), и вычисляет числа
(эту операцию выполняют все абоненты сети), и вычисляет числа
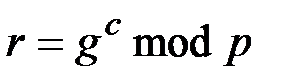 , (1.20)
, (1.20)
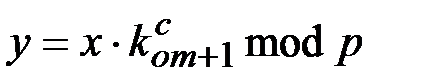 , (1.21)
, (1.21)
а затем передает пару 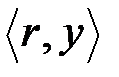 абоненту
абоненту 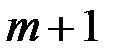 .
.
Абонент 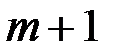 получив криптограмму
получив криптограмму 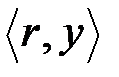 вычисляет исходный текст
вычисляет исходный текст
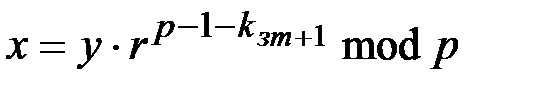 . (1.22)
. (1.22)
□ Подставим в (1.22) выражение (1.21) и получим
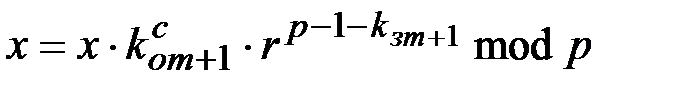 .
.
Теперь в полученное выражение подставим (1.19) и (1.20)
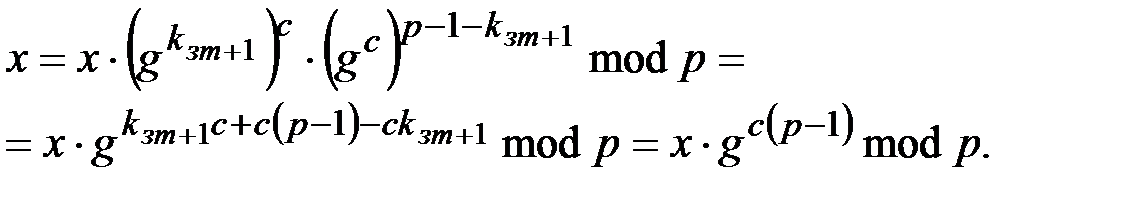
По теореме 1.4 (теорема Ферма) 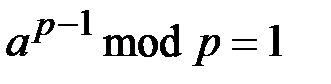 , тогда
, тогда
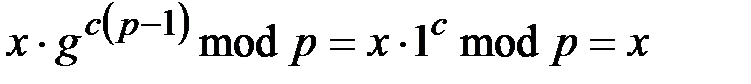 .■
.■
Злоумышленник должен определить закрытый ключ 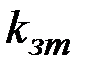 или отыскать число
или отыскать число 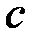 , но для этого ему необходимо решить задачу дискретного логарифмирования.
, но для этого ему необходимо решить задачу дискретного логарифмирования.
Особенностью криптосистемы Эль Гамаля является то, что объем передаваемой криптограммы в два раза превышает объем исходного сообщения. Это объясняется тем, что для вычисления криптограммы требуется выполнить операции (1.18) и (1.19). Следствием этого является большее, по сравнению с алгоритмом RSA, время шифрования и больший объем вычислений.
Рассмотрим пример шифрования при помощи алгоритма Эль Гамаля. Пусть требуется передать исходный открытый текст 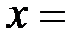 15 от абонента
15 от абонента 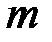 к абоненту
к абоненту 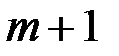 . Выберем в соответствии с (1.17) параметр
. Выберем в соответствии с (1.17) параметр 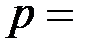 23 (
23 (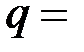 11). Определим параметр
11). Определим параметр 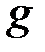 . Возьмем
. Возьмем 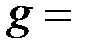 3, проверим:
3, проверим: 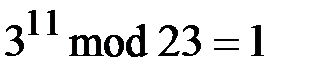 и значит такое число
и значит такое число 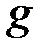 не подходит. Возьмем
не подходит. Возьмем 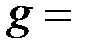 5, проверим:
5, проверим: 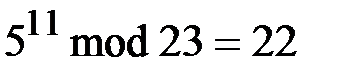 , такое число
, такое число 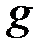 подходит. Таким образом, параметрами криптосистемы являются
подходит. Таким образом, параметрами криптосистемы являются 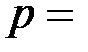 23 и
23 и 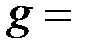 5. Пусть абонент
5. Пусть абонент 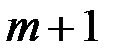 выбрал закрытый ключ
выбрал закрытый ключ 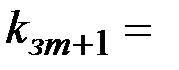 13 и вычислил открытый ключ
13 и вычислил открытый ключ  .
.
Абонент 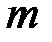 выбирает случайное число
выбирает случайное число  7 и вычисляет
7 и вычисляет
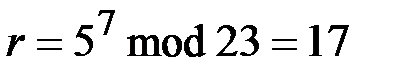 ,
,
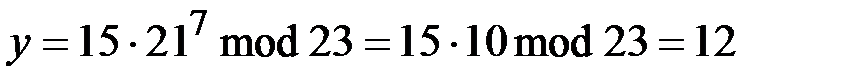 .
.
Абонент 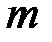 пересылает абоненту
пересылает абоненту 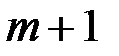 зашифрованное сообщение
зашифрованное сообщение 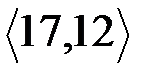 , которое абонент
, которое абонент 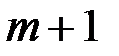 расшифровывает
расшифровывает
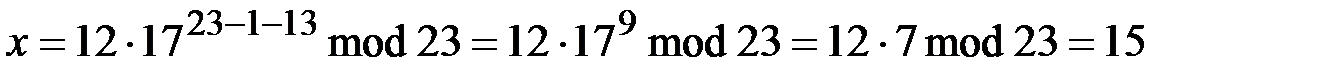 .
.
1.6. Криптосистема Рабина
Определение 1.11. Криптосистема с открытым ключом Рабина формально определяется следующим образом [6]:
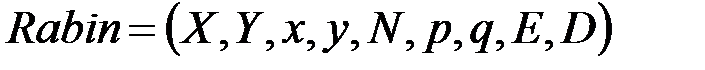 , (1.23)
, (1.23)
где 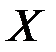 - множество открытых текстов,
- множество открытых текстов, 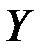 - множество криптограмм,
- множество криптограмм, 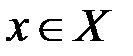 - некоторый открытый текст,
- некоторый открытый текст, 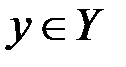 - некоторая криптограмма,
- некоторая криптограмма, 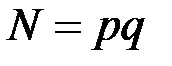 - RSA-модуль (является открытым ключом криптосистемы), где
- RSA-модуль (является открытым ключом криптосистемы), где 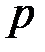 и
и 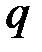 - секретные ключи криптосистемы,
- секретные ключи криптосистемы, 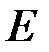 - функция шифрования,
- функция шифрования, 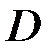 - функция расшифрования.
- функция расшифрования.
В криптосистеме Рабина используется RSA-модуль 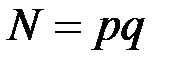 , в котором числа
, в котором числа 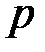 и
и 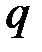 сравнимы с числом 3 по модулю 4:
сравнимы с числом 3 по модулю 4:
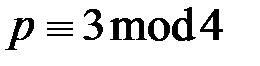 ,
, 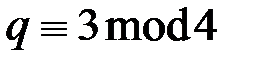 ,
,
что обеспечивает при знании разложения модуля возможность выполнения операции извлечения квадратного корня из квадратичных вычетов по модулю 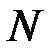 .
.
Шифрование осуществляется по формуле
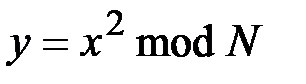 ,
,
причем должно выполняться условие: 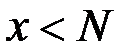 .
.
Процедура расшифрования состоит в извлечении квадратного корня из криптограммы. Предварительно вычисляются корни из 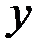 по модулям
по модулям 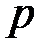 и
и 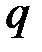 :
:
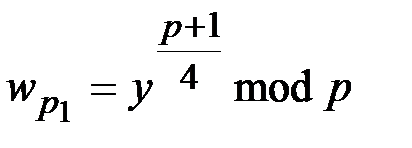 ,
, 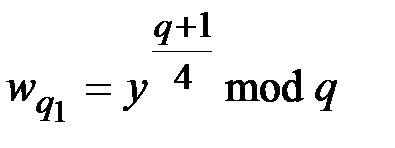 ;
;
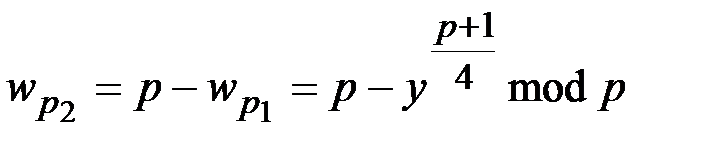 ,
,
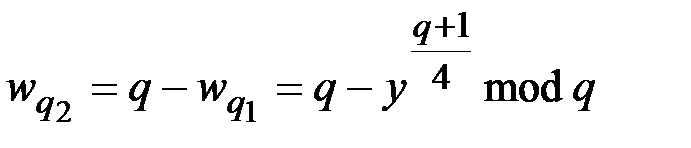 .
.
На основе полученных значений вычисляются четыре возможных корня из 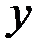 по модулю
по модулю 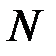 :
:
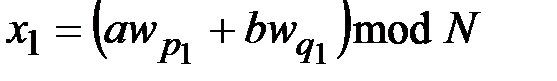 ,
,
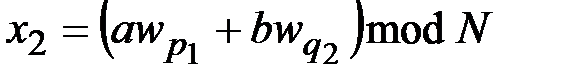 ,
,
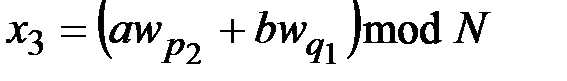 ,
,
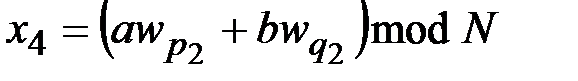 ,
,
где 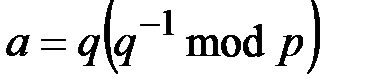 и
и 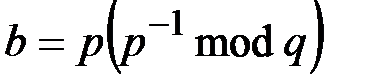 .
.
Как видно из представленных формул расшифрование неоднозначно, что является недостатком криптосистемы Рабина. Для обеспечения однозначности перед шифрованием к исходному открытому сообщению можно присоединить некоторую заранее оговоренную метку.
1.7. Криптосистемы на эллиптических кривых
Криптосистемы на эллиптических кривых – одно из новых направлений в криптографии. Эллиптические кривые давно изучаются математикой, но их использование в криптографии впервые было предложено Коблицом и Миллером в 1985 году. Прошедшие два с половиной десятилетия подтвердили эффективность этих криптосистем и привели к открытию множества их реализации. Основным достоинством криптосистем на эллиптических кривых является их более высокая стойкость по сравнению с традиционными асимметричными криптосистемами, при равных вычислительных затратах.
Детальное изучение эллиптических кривых требует знаний высшей алгебры, в особенности алгебраической геометрии. Рассмотрим математические основы теории эллиптических кривых, достаточных для понимания принципов построения и работы криптосистем [6-9].
Математические основы криптосистем на эллиптических кривых.
Определение 1.12. Кривая третьего порядка 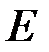 , задаваемая уравнением вида:
, задаваемая уравнением вида:
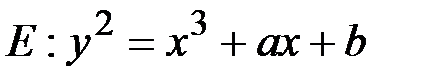 , (1.24)
, (1.24)
называется эллиптической кривой.
Наиболее общее определение эллиптической кривой дает уравнение Вейерштрасса [7].
Поскольку 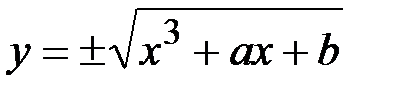 , график кривой симметричен относительно оси абсцисс. Для нахождения точек пересечения кривой
, график кривой симметричен относительно оси абсцисс. Для нахождения точек пересечения кривой 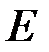 с осью абсцисс необходимо решить кубическое уравнение
с осью абсцисс необходимо решить кубическое уравнение
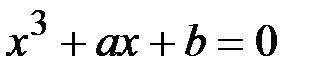 . (1.25)
. (1.25)
Это можно сделать с помощью известных формул Кордано. Дискриминант (1.25) имеет вид
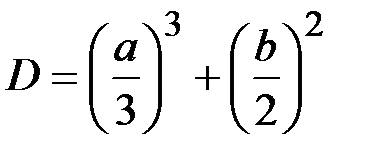 .
.
Если  , то (1.25) имеет три различных действительных корня
, то (1.25) имеет три различных действительных корня 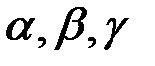 ; если
; если 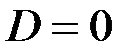 , то (1.25) имеет два различных действительных корня
, то (1.25) имеет два различных действительных корня 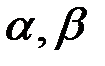 ; если
; если  , то (1.25) имеет один действительный корень
, то (1.25) имеет один действительный корень 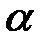 и два комплексно сопряженных корня (см. рис.1.3).
и два комплексно сопряженных корня (см. рис.1.3).
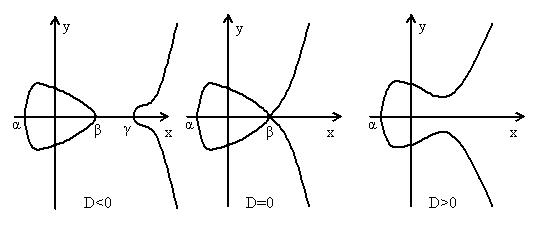
Рис.1.3. Эллиптическая кривая
Эллиптическая кривая, для которой 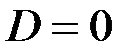 , называется сингулярной. Точка
, называется сингулярной. Точка 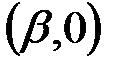 называется точкой сингулярности. Сингулярные эллиптические кривые в криптографии не используются, т.к. для них проблема дискретного логарифма эффективно решается [6,7]. Таким образом, для криптографических эллиптических кривых требуется выполнение условия
называется точкой сингулярности. Сингулярные эллиптические кривые в криптографии не используются, т.к. для них проблема дискретного логарифма эффективно решается [6,7]. Таким образом, для криптографических эллиптических кривых требуется выполнение условия
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 554; Нарушение авторских прав?; Мы поможем в написании вашей работы!