Российский стандарт ГОСТ Р 34.10-2012

Американский стандарт FIPS 186.

Рассмотрим только отличия американского стандарта ЭП от российского стандарта. Они сводятся к следующему:

1. Длина числа 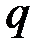берется равной 160 бит.

2. В качестве хеш-функции используется алгоритм SHA-1.

3. При генерации подписи на шаге 4 параметр 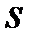вычисляется по формуле

.

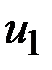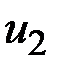4. При проверке подписи на шаге 3 вычисление и выполняются по формулам

, .

На рис. 2.2 представлен алгоритм формирования и проверки ЭП. Каждый пользователь должен иметь ключ формирования подписи 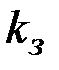и ключ проверки подписи 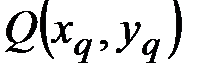. В алгоритме формирования ЭП вычисляется хеш-функция , на основании которой определяется число 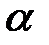, двоичным представлением которого является . Затем определяется число:

.

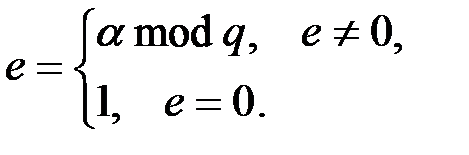Генерация случайного числа 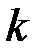, осуществляется при условии 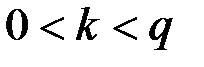. Затем вычисляется точка и оп ее абсциссе определяется число 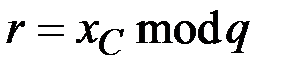. Точка 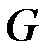удовлетворяет равенству 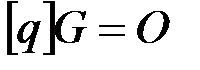. Далее вычисляется число

.

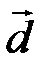ЭП представляет собой операцию конкатенации двух двоичных векторов и , соответствующих и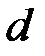

.

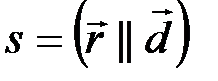Для проверки подписи выполняются аналогичные действия, но при этом вычисляются

,

, .

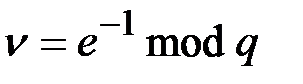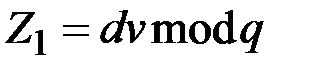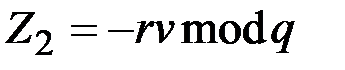Рис. 2.2. Алгоритм формирования и проверки ЭП ГОСТ Р34.10-2012

На основании этих числе вычисляется точка на эллиптической кривой 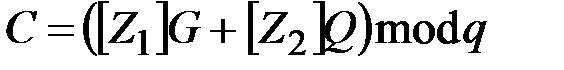и по ее абсциссе определяется число:

.

Если , то ЭП верна.

Параметрами рассмотренной схемы формирования ЭП являются: простое число - модуль эллиптической кривой; эллиптическая кривая E, задаваемая коэффициентами 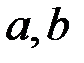; целое число - порядок группы точек эллиптической кривой E; простое число 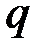- порядок циклической подгруппы группы точек эллиптической кривой E, для которого выполнены следующие:

точка 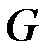удовлетворяющая равенству 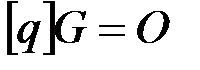; хеш-функция, определяемая стандартом ГОСТ Р.34.11-2012.

2.4. Электронная подпись на основе решения системы сравнений

Генерация ЭП, основанных на сложности дискретного логарифмирования, может быть осуществлена с использованием нового подхода [10], в котором оба элемента подписи и 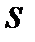представляются в одинаковом виде

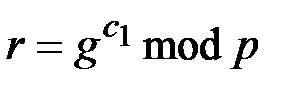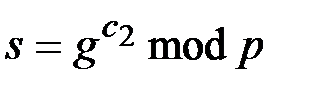, , (2.1)

где 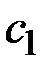и 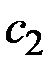вычисляются одновременно как одно из решений системы двух уравнений, записываемых в зависимости от вида проверочного соотношения.

Идея этого подхода состоит в том, чтобы сделать вычислительно невозможным вычисление одного из параметров и 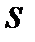при заранее заданном значении второго параметра. Параметры и и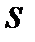спользуются как аргументы двух различных функци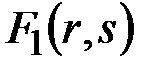й и 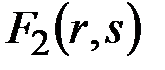. При определенных ограничениях на значения аргументов их можно изменять таким образом, что значение функции 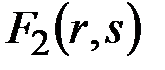будет оставаться неизменным. При этом значение функции 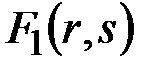должно изменяться таким образом, что можно подобрать пару значений и 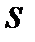, при которых будет выполняться некоторое проверочное соотношение. 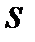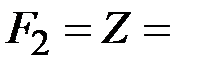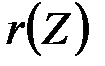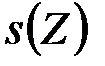Таким образом, в определенной области пар значений и имеем const, поэтому проверочное соотношение в принципе может быть упрощено, так, что при определенном его виде можно вычислить подпись и , зависящую от .

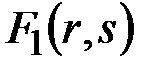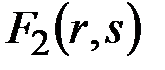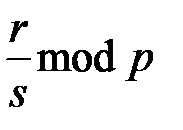При составлении конкретных вариантов ЭП могут быть использованы следующие пары функций , :

, или , ;

, ;

, ;

, ,

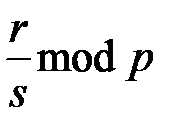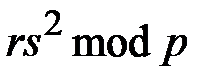где .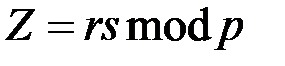

При этом значения и 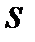предполагается выражать через 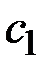и 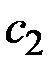в виде (2.1).

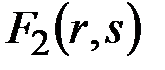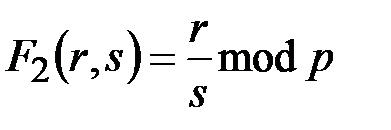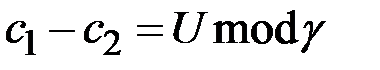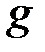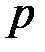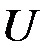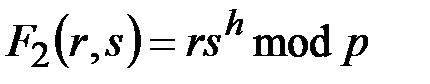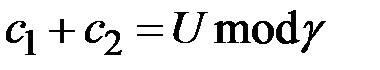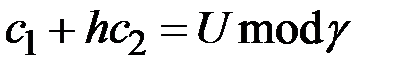Если функция имеет вид: , то условие постоянства значения функции запишется в виде: , где - некоторый показатель, к которому число относится по модулю ; - случайно выбираемое число. В случае если или условие постоянства значения функции запишется в виде: и , соответственно. При этом предполагается следующие варианты проверочных соотношений:

,

,

,

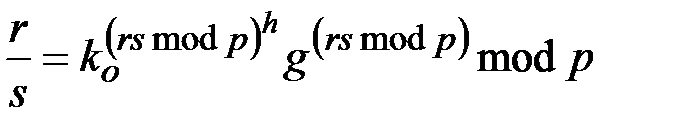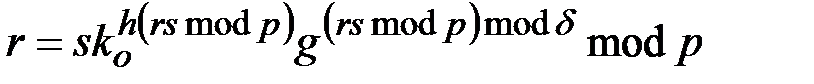где - произвольное простое число длины 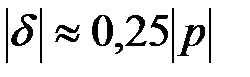. Операция определяет сжимающую функцию 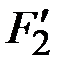, значение которой остается постоянной, если значение 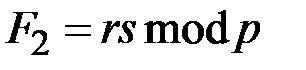не изменяется. Это позволяет получить и использовать в проверочном соотношении две функции, зависящие от параметров 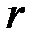и 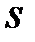, прием такие, что их значения фиксируются одновременно при условии, что параметры 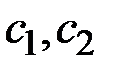удовлетворяют определенным условиям.

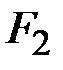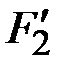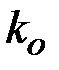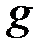Необходимость использования пары одновременно фиксируемых функций и связана с тем, что в проверочном соотношении требуется задать показателя степени элементов и , зависящие от 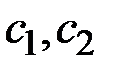. Если это условие не выполнено, то ЭП можно легко подделать путем включения фиксированной степен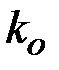и или 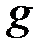как дополнительного множителя в представлении одного из параметров 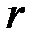и .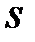

Для примера рассмотрим ЭП с проверочным соотношением

,

которое может быть представлено в другом виде

.

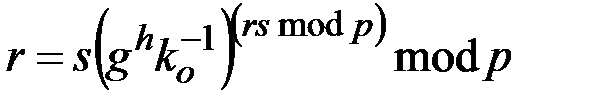Элементы подписи определяются на основе соотношений

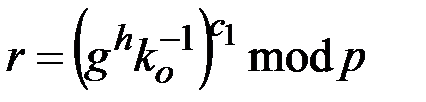, (2.2)

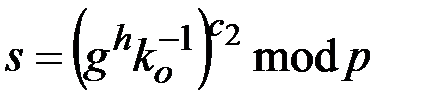. (2.3)

При

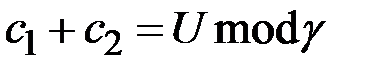, (2.4)

значение 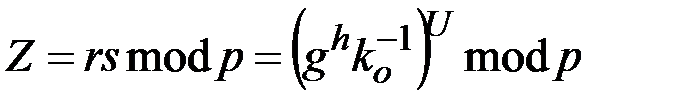является фиксированным и условием выполнимости проверочного соотношения является

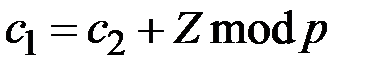. (2.5)

Действительно, если (2.4) и (2.5) выполняются, то получаем

Таким образом, ЭП может быть вычислена без использования секретного ключа путем совместного решения уравнения сравнений (2.4) и (2.5) и последующего вычисления элементов ЭП по формулам (2.2) и (2.3).

В рассмотренном подходе по ключу и подписи 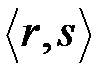вычислительно крайне сложно найти , которое выбирается произвольным. Для вычисления 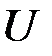требуется вычислить и , и , однако, для этого необходимо решить задачу дискретного логарифмирования.

Дальнейшим развитием ЭП на основе решения системы сравнений является ЭП вида 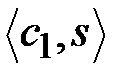. Отказ от использования значения 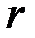в качестве элемента подписи в ЭП вида 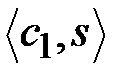не только устраняет возможность подделки подписи на основе замены переменных, но и дает ряд преимуществ, которые заключаются в следующем.

1. Отказ от одной из двух фиксируемых функци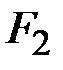й и 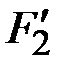, поскольку число 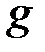возводится непосредственно в степень , которая приобретает конкретное значение только после решения системы сравнений. Теперь достаточно включения в проверочные соотношения только одного множителя 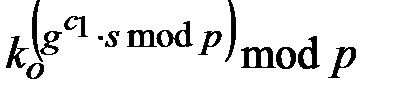с показателем степени, определяемым после решения системы сравнений. Это обеспечивает упрощение вида проверочных соотношений.

2. Размер ЭП может быть существенно сокращен, если в качестве числа 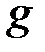использовать число, относящееся по модулю 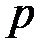к простому показателю , длина которого существенно меньше длины , например 160…256 бит.

3. Появляется возможность реализации ЭП, в которой условие фиксирования задается сравнениями, включающими произведение или отношение значений , и .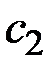

Примером ЭП вида 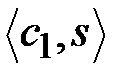может служить подпись, вычисляемая на основе соотношений

, ,

.

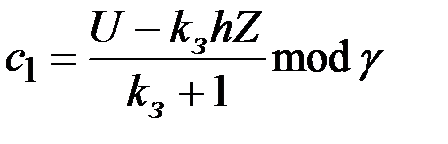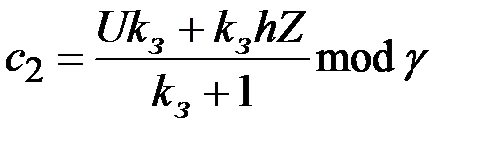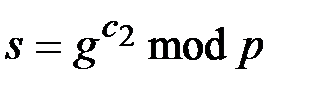Система решаемых сравнений и формула вычисления 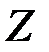имеют вид

.

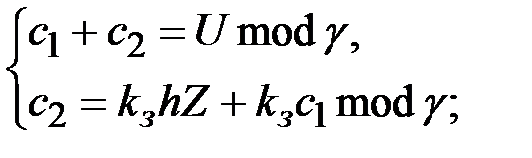
Проверочное соотношение

.

2.5. Коллективная и композиционная электронная подпись

Одной из актуальных задач в области аутентификации электронных документов с помощью ЭП является проблема одновременного подписания документа (например, контракта) группой людей на расстоянии. Эта задача естественным образом решается путем применения алгоритмов коллективной ЭП [10]. Коллективная ЭП формируется на основе параметров, вырабатываемых всеми подписывающими, причем подлинная коллективная ЭП может быть сформирована только для случая, когда документ подписан всеми участниками протокола коллективной ЭП. Вычислительно невозможно сформировать урезанную коллективную ЭП, т.е. создать такую ЭП, которая соответствовала бы меньшему числу пользователей. Это свойство решает проблему подписания одного документа несколькими пользователями.

На практике возникают ситуации, когда требуется одновременно подписать пакет документов, причем коллектив подписывающих для одного документа может отличаться от коллектива подписывающих для другого документа. Решение этой задачи требует другого протокола ЭП. Таким протоколом является протокол композиционной ЭП [10]. Композиционная ЭП является, по существу, дальнейшим развитием схемы коллективной ЭП. Композиционная ЭП позволяет различным пользователям или группам пользователей подписывать одновременно различное количество разных документов.

Главное отличие коллективной и композиционной ЭП состоит в различии процедур формирования коллективного открытого ключа. В случае коллективной ЭП коллективный открытый ключ является функцией открытых ключей отдельных пользователей, а в случае композиционной ЭП – функцией открытых ключей отдельных пользователей и значений хеш-функций подписываемых документов.

Протоколы коллективной и композиционной ЭП реализовываются на основе различных алгоритмов и стандартов ЭП. Например, на основе алгоритмов ЭП основанных на задаче дискретного логарифмирования, на сложности задачи факторизации, на основе стандарта ГОСТ 34.10.94 и других стандартов.

Для примера рассмотрим алгоритмы коллективной и композиционной ЭП основанных на сложности задачи факторизации.

В пункте 2.1 рассмотрена ЭП с использованием алгоритма RSA. Открытым ключом является пара чисел 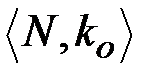, а тройка чисел 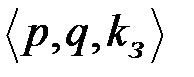- является секретной. Формирование и проверка подписи выполняется по формулам

, .

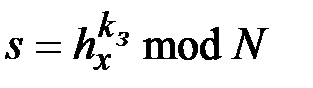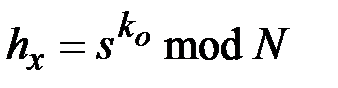Размер хеш-функции составляет обычно 160…256 бит, что значительно меньше размера модуля .

Пусть коллектив пользователей 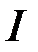, , 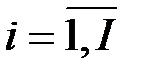желает подписать документ 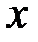, представленный хеш-функцией 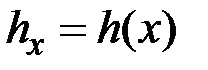. Коллективная подпись может быть сформирована следующим образом.

1. Открытые ключи пользователей упорядочиваются по возрастанию модуля, т.е. .

2. Последовательно формируются подписи: 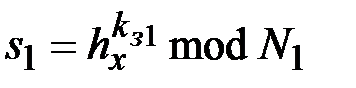, , 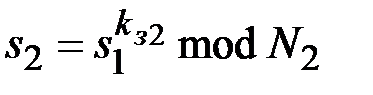…, ,…, 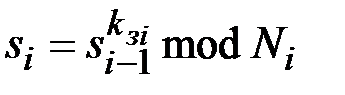. Значение 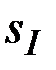является коллективной ЭП.

3.Проверка коллективной подписи выполняется в обратном порядке: , , 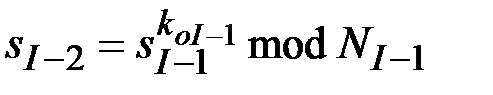…, , 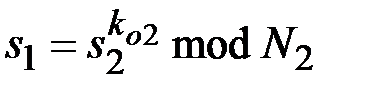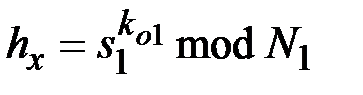. Если 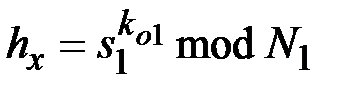справедливо, то коллективная ЭП подлинная.

Композиционная подпись к документам , , 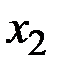…, , 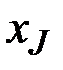представленным хеш-функциями , , 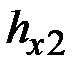…, , может быть сформирована следующим образом.

1. Открытые ключи пользователей упорядочиваются по возрастанию модуля, т.е. .

2. Последовательно формируются подписи: , ,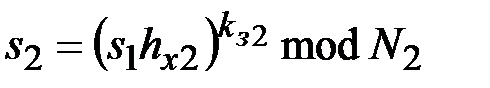.., ,..., . 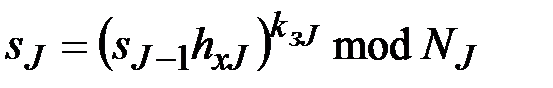Значение 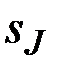является композиционной ЭП.

3. Проверка композиционной ЭП выполняется следующим образом: , , 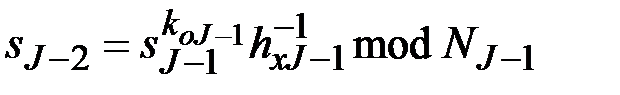…, , 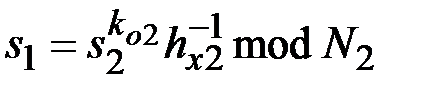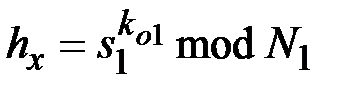. Если 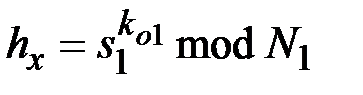выполняется, то композиционная подпись подлинная. Каждый пользователь в этом случае подписывает соответствующий ему документ. Размер композиционной подписи равен длине модуля , хранить хеш-функции от документов не нужно, т.к. их можно всегда вычислить.

В рассмотренном протоколе композиционной подписи подпись может быть сформирована любым подмножеством пользователей .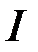

2.6. Слепая электронная подпись

Слепая электронная подпись является разновидностью ЭП и отличается тем, что подписывающая сторона не может точно знать содержимое подписываемого документа [2,10]. Понятие слепой подписи введено Дэвидом Чаумом, им же предложена первая реализация алгоритма слепой ЭП.

Основная идея слепой электронной подписи заключается в следующем. Отправитель А посылает документ стороне В, который В подписывает его и возвращает А. Используя полученную подпись, сторона А может вычислить подпись стороны В. По завершении этого протокола сторона В ничего не знает ни о документе, ни о подписи под этим документом. Эту схему можно сравнить с конвертом, в котором размещён документ и копировальный лист. Если подписать конверт, то подпись отпечатается на документе, и при вскрытии конверта документ уже будет подписан.

Таким образом цель алгоритма слепой электронной подписи состоит в том, чтобы воспрепятствовать подписывающему лицу В ознакомиться с сообщением стороны А, которое он подписывает, и с соответствующей подписью под этим сообщением.

Слепая электронная подпись Чаума. Слепая электронная подпись Чаума основана на криптосистеме RSA. Пусть пользователь А желает подписать документ у пользователя В таким образом, чтобы последний не мог прочесть подписываемый документ. Для этого необходимо выполнить следующее.

1. Пользователь А генерирует случайное простое число 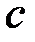взаимно простое с 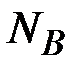, где 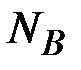- часть открытого ключа пользователя В.

Затем пользователь А вычисляет значение

,

и предъявляет его на подпись пользователю В, чтобы последний подписал 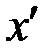в соответствии со стандартной процедурой ЭП RSA. Пользователь В не может прочесть документ , поскольку оно преобразовано путем наложения «разового» ключа 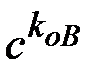с использованием операции модульного умножения. Таким образом, пользователь А «маскирует» документ при помощи множителя, который иногда называют маскирующим множителем.

2. Пользователь В подписывает документ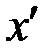

.

Заметим, что по значению к сообщению 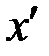пользователь В не имеет возможности вычислить . Однако, по значению пользователю А легко вычислить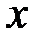

.

Т.е. после получения значения

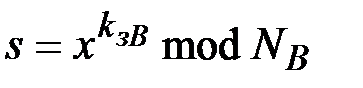
пользователь А должен держать его в секрете от подписавшего.

3. После получения от пользователя В значения , используя расширенный алгоритм Евклида, пользователь А вычисляет для числа 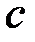мультипликативно обратный элемент 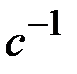по модулю 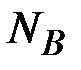и формирует подпись пользователя В к исходному документу

.

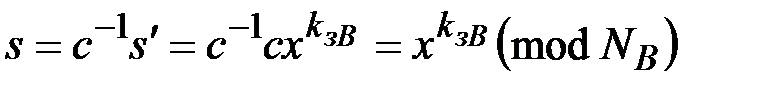В настоящее время слепые ЭП находят широкое применение в сфере цифровых денег, в системах тайного электронного голосования. Для примера рассмотрим применение слепой ЭП в системах тайного электронного голосования.

Схема применения слепой ЭП состоит в следующем. Избиратель подготавливает избирательный бюллетень со своим выбором, который он сделал, шифрует его секретным ключом, и маскирует его. Далее избиратель подписывает избирательный бюллетень и посылает его валидатору. Валидатор проверяет, что подпись принадлежит зарегистрированному избирателю, который еще не голосовал. Если избирательный бюллетень действителен, валидатор подписывает избирательный бюллетень и возвращает его избирателю. Избиратель удаляет маскировку, раскрывая таким образом зашифрованный избирательный бюллетень, подписанный валидатором. Далее избиратель посылает избирательный бюллетень счётчику, который проверяет подпись на зашифрованном избирательном бюллетене. Если избирательный бюллетень действителен, счётчик размещает его в списке, который будет издан после всего голосования. После того, как список издан, избиратели проверяют, что их избирательные бюллетени находятся в списке и посылают счётчику ключи расшифрования, необходимые, чтобы открыть их избирательные бюллетени. Счётчик использует эти ключи для расшифрования избирательных бюллетеней и добавляет голос к общему числу. После выборов счётчик издает ключи расшифрования наряду с зашифрованными избирательными бюллетенями, чтобы избиратели могли независимо проверить выбор.

Существует много алгоритмов слепой ЭП, отличающиеся различной степенью сложности и возможностями по применению. Чаум, например, разработал целое семейство более сложных алгоритмов слепой подписи под общим названием неожиданные слепые подписи. Подробно о слепых ЭП можно прочесть в [10].

Контрольные вопросы:

1. Дайте определение электронной подписи. Каковы требования к электронной подписи?

2. Поясните алгоритмы формирования и проверки электронной подписи RSA и Эль Гамаля. В чем их отличие?

3. Какие стандарты электронных подписей существуют в настоящее время?

4. Дайте определение слепой электронной подписи.

5. Назовите способы сокращения длины электронной подписи. В чем их суть?

6. Дайте определение коллективной и композиционной электронной подписи. В чем их отличие?

Дата добавления: 2014-12-26