Пример определения достоверности различий между средними величинами по критерию Стьюдента

Условие задачи: сравнение средней частоты сердечных сокращений (ЧСС) детей 1‑го года жизни в отделениях №1, №2 (см. раздел III).

Задание: а) оценить достоверность различий между средним пульсом пациентов 1‑го и 2-го отделений с помощью доверительных границ;

б) вычислить критерий Стьюдента для сравнения ЧСС детей в этих отделениях, сделать вывод о достоверности различий средних величин.

Решение: Запустите программу Excel, откройте требуемый файл в папке своей учебной группы под именем «Статистика–Фамилии студентов». Создайте НОВЫЙ лист, переименуйте его, обозначив названием «Крит_Стьюдента». На этом листе введите данные и решение задачи, как показано ниже, сохраните изменения и покажите результат работы преподавателю.

а) доверительные границы колебаний средних в каждом отделении при уровне значимости p <0,05, т.е. с вероятностью прогноза более 95%, составляет M ±2 m, где M – средняя арифметическая, m – ошибка репрезентативности.

По условию задачи в 1-м отделении M₁ =121,9, m ₁ =1,64. Т.е. 121,9 ± 2*1,64 = 121,9 ± 3,28 уд/мин. В ячейке таблицы Excel вводятся формулы =121,9+3,28 и =121,9-3,28. Получаем доверительные границы колебаний средней частоты пульса в 1-м отделении от 118,62 до 125,18 уд/мин.

Аналогично определяем доверительные границы средней ЧСС во 2-м отделении. По условию задачи M₂ =126,2, m₂ =2,04. Т.е. 126,29 ± 2 * 2,04 = 126,2 ± 4,08 уд/мин. Формулы вычисления =126,29+4,08 и =126,29-4,08. Получаем доверительные границы колебаний средней частоты пульса в 2-м отделении от 122,21 до 130,37 уд/мин.

Величина доверительных границ частоты пульса в 2-х отделениях больницы позволяют утверждать, что при повторных экспериментах в 95% случаях будут получены средние величины, укладывающиеся в пределах вычисленных значений границ в 1-м отделении от 118,62 до 125,18 уд/мин, во 2-ом - от 122,21 до 130,37 уд/мин. Поскольку доверительные границы этих отделений имеют пересечение верхней границы 1-го и нижней границы 2-го отделений, можно предположить, что полученная разница средних является случайной и может не повториться в следующих экспериментах.

б) оценка достоверности различий средней частоты пульса детей, поступающих в 1‑е и 2-е отделение больницы по критерию Стьюдента.

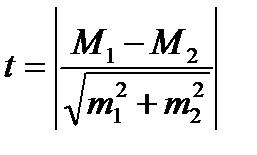Формула вычисления критерия Стьюдента:,

где: M₁ – средняя арифметическая 1-го вариационного ряда - 121,8,

M₂ – средняя арифметическая 2-го вариационного ряда - 126,2,

m₁ – ошибка репрезентативности 1-го вариационного ряда - 1,64,

m₂ – ошибка репрезентативности 2-го вариационного ряда - 2,04.

В программе Excel эта формула принимает вид:

=(121,8 – 126,2)/КОРЕНЬ(1,64^2+2,04^2) = -1,64667.

Модуль числа может быть получен с помощью функции =ABS(Число) = ABS(-1,64667) = 1,64667. Округление числа выполняется функцией =ОКРУГЛ(Число; Разрядность) = ОКРУГЛ(1,64667;2) = 1,65.

Вычисленное значение t -критерия (-1,65) оценивается по модулю числа (1,65) в сравнении с критическим значением, которое при числе наблюдений n >30 составляет 2. При числе наблюдений n <30 критическое значение находят по таблицам Стьюдента при степенях свободы df = n₁ + n₂ – 2 = 16 + 17 – 2 = 31. В программе Excel критическое значение критерия Стьюдента вычисляется функцией = СТЬЮДРАСПОБР(Уровень значимости p; Степени свободы df) =

= СТЬЮДРАСПОБР(0,05;(16+17-2)) = 2,04.

Если t >2,04 – статистическая гипотеза о равенстве средних с уровнем значимости p<0,05 опровергается, следовательно, истинной будет являться гипотеза об их различии. Если t <2,04 – гипотеза равенства средних подтверждается.

В нашем примере получаем: t = 1,65 < 2,04.

Если в сравниваемых вариационных рядах равное число наблюдений (n ₁= n ₂), программа Excel позволяет выполнить вычисления при помощи функции =ТТЕСТ(Диапазон1;Диапазон2;H;Тип), где:

Диапазон1 – первый вариационный ряд (множество данных);

Диапазон2 – второй вариационный ряд (множество данных);

H – число хвостов распределения (1 или 2), как правило, используется число 2. Если Н = 1, то функция ТТЕСТ использует одностороннее распределение, при Н = 2 используется двустороннее распределение.

Тип – цифра модификации теста 1, 2 или 3. Как правило используется цифра 3. Если указана цифра 1 – это парный тест для связанных выборок, 2 – двухвыборочный с равными дисперсиями, 3 – двухвыборочный с неравными дисперсиями.

В большинстве задач статистической обработки медицинских данных эта функция применяется с параметрами =ТТЕСТ(Диапазон1;Диапазон2;2;3), что считается более грубой оценкой, но вполне достаточной для опровержения нулевой гипотезы.

Функция ТТЕСТ возвращает уровень значимости основной гипотезы при сравнении 2-х числовых массивов, вычисленный по критерию Стьюдента. Он выражает вероятность того, что две выборки взяты из генеральных совокупностей, которые имеют одно и то же среднее.

В нашем случае можно выполнить вычисление этой функцией на основе данных 16-и человек в каждой группе. Получаем опытный уровень значимости 0,12. Это означает, что выдвинутая гипотеза о равенстве средних в генеральной совокупности подтверждается с вероятностью 12%. Поскольку значение опытного уровня значимости больше принятого критического уровня (p =0,05 или 5%), то альтернативная гипотеза о различии средних величин не может быть принята, и значит, различия не подтверждены. В такой ситуации можно провести дополнительное исследование с теми же условиями опыта, но с увеличенным числом единиц наблюдения, что на более качественном уровне подтвердит или опровергнет рабочую гипотезу.

Вывод: Различия средней частоты пульса пациентов 1-го и 2-го отделений НЕдостоверны. Значит, более высокая средняя частота пульса во 2-м отделении больницы (126,2 уд/мин) по сравнению с ЧСС в 1-м отделении (121,9 уд/мин) не подтверждается при уровне значимости p =0,05.

Дата добавления: 2014-12-23